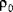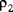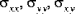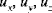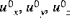Shell Property Equations
This document provides a very brief description of how the mechanical properties of shells are represented mathematically in Creo Simulate. This document also defines the terminology used to describe shell properties and shell results within Creo Simulate.
This document is divided into the following sections:
Topic
Overview
The formulae given in this document express the fundamental relationships between shell forces, moments, strains, curvature changes, and shell properties and results. These formulae are provided to unambiguously define the conventions used to describe the various modeling and results data for shells.
You specify properties that define the mechanical behavior of laminate shells on the laminate stiffness version of the
Shell Property Definition dialog box. See
About Shell Properties for more information. At the point for which you want to see results, you define the following properties relative to the material orientation:
• shell extensional stiffnesses
• shell transverse shear stiffnesses
• shell extensional-bending coupling stiffnesses
• shell bending stiffnesses
• shell resultant thermal moment coefficients
• shell resultant thermal force coefficient
• mass per unit area
• rotary inertia per unit area
You can review the following results quantities with respect to the material orientation at the point of interest or with respect to a coordinate system. See
Relative Results for more information.
• rotation of shell midsurface about the X and Y axes
• midsurface strain
• curvature change of the shell midsurface
• shell resultant moment
• shell resultant force
• shell transverse shear force
• stress
• displacement of the shell midsurface
See the
List of Symbols for the symbols that represent these terms.
These formulae and their descriptions are not meant to be a tutorial for the analysis of shells. More detailed information concerning the modeling of laminated or orthotropic shells may be found in the texts by Jones (1), Reddy (2), Tsai (3), Ugural (4) and others. The
Bibliography describes these texts.
The figures and equations presented in this section are given for flat shells, or plates. The engineering concepts presented here generalize to curved shells, but the mathematical descriptions of curved shells are more complicated and will not be given.
Formulae for Calculating Shell Properties
A shell is a section of your Creo Simulate model that is thin in comparison to its width and length. It is computationally efficient to model the thin regions of your structure with shells. This efficiency results, in part, from a basic assumption concerning the behavior of shells. That is, that the mechanical behavior of a shell can be approximated by describing the mechanical behavior of the midsurface of the shell.
Thus, the displacement of a shell can be described by the displacement and rotation of its midsurface, the straining of a shell can be described by the straining and curvature changes of its midsurface, and the equilibrium of a shell can be described by the equilibrium of stresses integrated through the thickness of the shell.
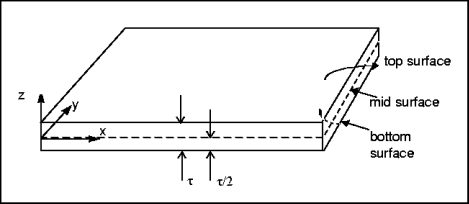
The figure below shows a flat rectangular shell, the edges of which are aligned with the X and Y axes of a Cartesian coordinate system. The XY plane of this coordinate system is halfway between the top and bottom surfaces of the shell; that is, the midsurface of the shell is at z=0. The shell has thickness t, so that the top surface is at z = t/2 and the bottom surfaces is at z = –t/2, as the following figure illustrates:
As mentioned above, it is assumed that the displacement of any point (x, y, z) in the shell can be expressed in terms of the displacement and rotation of the point (x, y, 0) on the midsurface of the shell. Specifically, it is assumed that:
where:
• 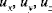
are the components of displacement in the x, y, and z directions, respectively
• 
are the components of displacement of the midsurface
• 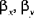
are the (small) rotations of the midsurface about the x and y axes, respectively
Similarly, the strain components
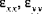
and
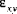
of any point (x,y,z) can be expressed in terms of the midsurface (or membrane) strains (

) and curvature changes (
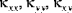
) as:
Note that Equation (A.2) contains the tensor shear strain components,
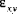
and

, and not the engineering shear strain components, which are twice the values of the tensor shear strain components.
For flat shells, the tensor shear strain components are:
and
The shell resultant forces (
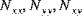
), the shell resultant moments (
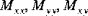
), and the shell transverse shear forces (
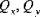
) are obtained by integrating the stress components
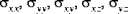
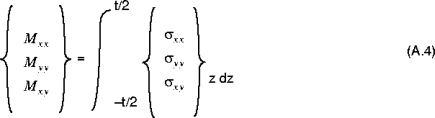
through the thickness of the shell. The shell resultant forces are given by:
The shell resultant moments are given by:
The shell transverse shear forces are given by:
The following figure illustrates the sign conventions employed for the resultant forces and moments, and transverse shear forces. Note that a positive moment,
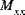
, induces positive strain,
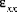
, in the top half of the shell (z > 0) and negative strain in the bottom half of the shell (z < 0).
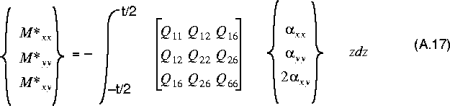
The relationship between the shell resultants, and the midsurface strains and curvature changes are given by:
and:
In equation (A.6), the quantities
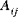
(where i,j = 1, 2, 6) are called the shell extensional stiffnesses, the quantities
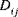
are called the bending stiffnesses, the quantities
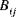
are called the extensional-bending coupling stiffnesses, and the quantities

(where k,l = 4,5) are called the transverse shear stiffnesses. The quantities
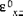
and
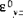
are the transverse shear strains on the midsurface. The quantities
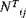
and

are the resultant thermal forces and moments respectively.
The shell stiffness and thermal resultants introduced in Equations (A.6) and (A.7) are defined by integrating the material properties of the shell through the thickness of the shell. The extensional, bending, and extensional-bending stiffnesses are given by:
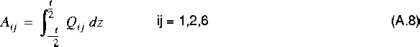
and:
and:
where
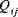
are the reduced stiffnesses of the material.
The transverse shear stiffness is given by:
where:
• 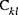
are (non-reduced) stiffnesses of the material, and
• 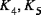
are the shear correction coefficients, which for a homogeneous shell are often taken to be
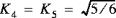
.
Note that if the material of the shell is distributed symmetrically about the midsurface, then the integral in Equation (A.9) vanishes and the extensional-bending coupling stiffnesses
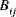
are identically zero.
The resultant thermal forces and moments are given by:
and:
where:
• 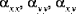
are the coefficients of thermal expansion of the material, and
• 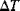
is the change in temperature from the stress-free state.
If the change in temperature is uniform through the thickness of the shell, then the
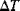
in Equations (A.12) and (A.13) may be removed from the integral, resulting in Equations (A.14) and (A.15):
where

are called the shell resultant thermal coefficients, which are given by:
The mass properties for shells are also obtained by integrating the material property data through the thickness of the shell. The mass per unit area,
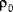
, is given by:
where
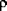
is the density of the material.
The rotary inertia per unit area,
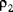
, is given by:
List of Symbols
The following table defines the symbols used in this document:
Symbol | Definition |
| coefficients of thermal expansion |
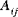 (i,j = 1,2,6) | shell extensional stiffness |
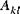 (k,l = 4,5) | shell transverse shear stiffness |
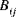 (i,j = 1,2,6) | shell extensional-bending coupling stiffness |
| rotation of shell midsurface about the X and Y axes |
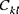 (k,l = 4,5) | material stiffness |
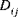 (i,j = 1,2,6) | shell bending stiffness |
| temperature change |
| strain |
| midsurface (or membrane) strain |
| curvature change of the shell midsurface |
 (k,l = 4,5) | shear correction coefficients |
| shell resultant moment |
| shell resultant thermal moment |
| shell resultant thermal moment coefficient |
| shell resultant force |
| shell resultant thermal force |
| shell resultant thermal force coefficient |
| shell transverse shear force |
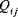 (i,j = 1,2,6) | material reduced stiffness |
| mass per unit area |
| rotary inertia per unit area |
| stress |
t | shell thickness |
| displacement |
| displacement of the shell midsurface |
x, y | midsurface coordinates |
z | coordinate perpendicular to the shell midsurface |
Bibliography
1. Jones, Robert M. Mechanics of Composite Materials. Washington, DC: Scripta Book Company, 1975.
2. Reddy, J.N. Energy and Variational Method in Applied Mechanics. New York: John Wiley & Sons, 1984.
3. Tsai, S. W. and H. T. Hahn Introduction to Composite Materials. Westport, CT: Technomic Publishing Co., 1980.
4. Ugural, A. C. Stresses in Plates and Shells. New York: McGraw-Hill Book Company, 1981.

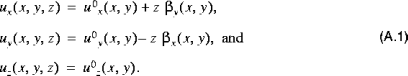
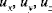 are the components of displacement in the x, y, and z directions, respectively
are the components of displacement in the x, y, and z directions, respectively are the components of displacement of the midsurface
are the components of displacement of the midsurface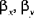 are the (small) rotations of the midsurface about the x and y axes, respectively
are the (small) rotations of the midsurface about the x and y axes, respectively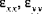 and
and 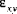 of any point (x,y,z) can be expressed in terms of the midsurface (or membrane) strains (
of any point (x,y,z) can be expressed in terms of the midsurface (or membrane) strains ( ) and curvature changes (
) and curvature changes (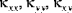 ) as:
) as:
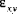 and
and  , and not the engineering shear strain components, which are twice the values of the tensor shear strain components.
, and not the engineering shear strain components, which are twice the values of the tensor shear strain components.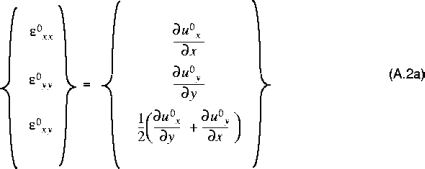
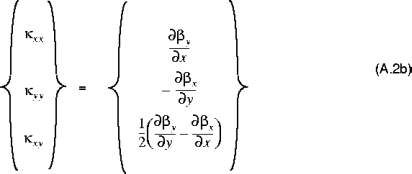
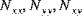 ), the shell resultant moments (
), the shell resultant moments (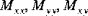 ), and the shell transverse shear forces (
), and the shell transverse shear forces (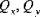 ) are obtained by integrating the stress components
) are obtained by integrating the stress components 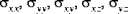 through the thickness of the shell. The shell resultant forces are given by:
through the thickness of the shell. The shell resultant forces are given by: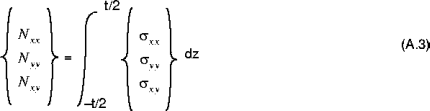
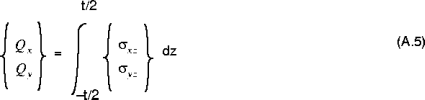
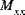 , induces positive strain,
, induces positive strain, 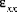 , in the top half of the shell (z > 0) and negative strain in the bottom half of the shell (z < 0).
, in the top half of the shell (z > 0) and negative strain in the bottom half of the shell (z < 0).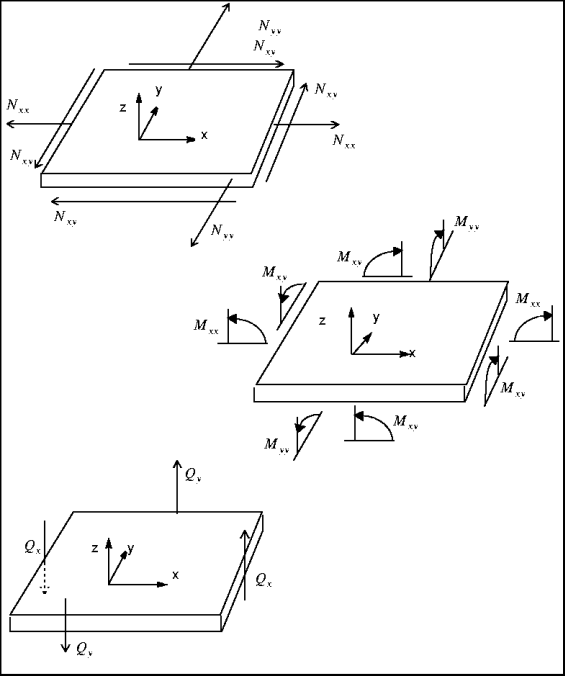
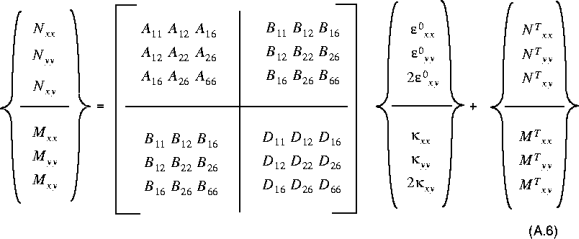
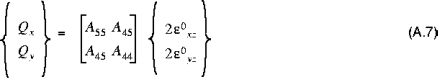
 (where i,j = 1, 2, 6) are called the shell extensional stiffnesses, the quantities
(where i,j = 1, 2, 6) are called the shell extensional stiffnesses, the quantities 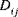 are called the bending stiffnesses, the quantities
are called the bending stiffnesses, the quantities 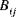 are called the extensional-bending coupling stiffnesses, and the quantities
are called the extensional-bending coupling stiffnesses, and the quantities  (where k,l = 4,5) are called the transverse shear stiffnesses. The quantities
(where k,l = 4,5) are called the transverse shear stiffnesses. The quantities 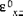 and
and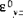 are the transverse shear strains on the midsurface. The quantities
are the transverse shear strains on the midsurface. The quantities 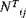 and
and  are the resultant thermal forces and moments respectively.
are the resultant thermal forces and moments respectively.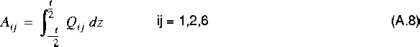 and:
and: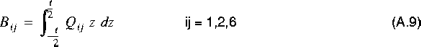
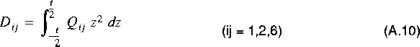
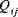 are the reduced stiffnesses of the material.
are the reduced stiffnesses of the material.
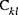 are (non-reduced) stiffnesses of the material, and
are (non-reduced) stiffnesses of the material, and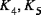 are the shear correction coefficients, which for a homogeneous shell are often taken to be
are the shear correction coefficients, which for a homogeneous shell are often taken to be 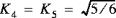 .
.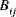 are identically zero.
are identically zero.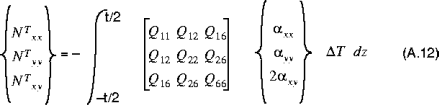
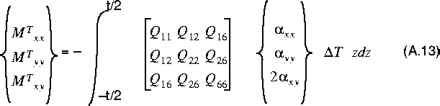
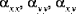 are the coefficients of thermal expansion of the material, and
are the coefficients of thermal expansion of the material, and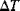 is the change in temperature from the stress-free state.
is the change in temperature from the stress-free state.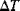 in Equations (A.12) and (A.13) may be removed from the integral, resulting in Equations (A.14) and (A.15):
in Equations (A.12) and (A.13) may be removed from the integral, resulting in Equations (A.14) and (A.15):
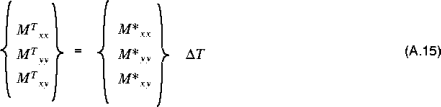
 are called the shell resultant thermal coefficients, which are given by:
are called the shell resultant thermal coefficients, which are given by: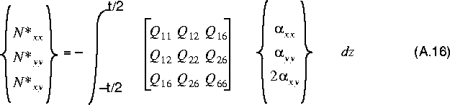
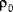 , is given by:
, is given by:
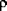 is the density of the material.
is the density of the material.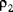 , is given by:
, is given by:
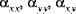
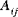 (i,j = 1,2,6)
(i,j = 1,2,6)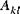 (k,l = 4,5)
(k,l = 4,5)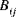 (i,j = 1,2,6)
(i,j = 1,2,6)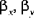
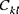 (k,l = 4,5)
(k,l = 4,5)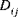 (i,j = 1,2,6)
(i,j = 1,2,6)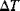
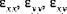
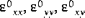
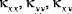
 (k,l = 4,5)
(k,l = 4,5)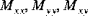
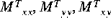
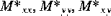
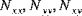
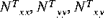


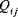 (i,j = 1,2,6)
(i,j = 1,2,6)