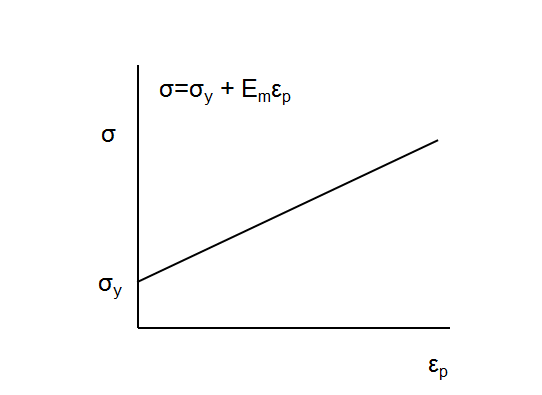
Linear Hardening Law
When the stress is below the tensile yield stress, the material behaves elastically. After yielding has occurred, for the linear hardening law the relation between stress and strain can be represented by the graph shown below:
The following equation represents the linear hardening law:
σ = σy + Em εp
where:
• εp represents strain
• Em is the slope of the stress-strain curve called the tangent modulus. The tangent modulus has the same units as Young's modulus.
Fit the Tangent Modulus to the curve if you use test data to define the material. If you clear the Define By Tests check box, you must enter a constant value for Tangent Modulus.
The value of the tangent modulus is greater than 0 but less than Young’s modulus.