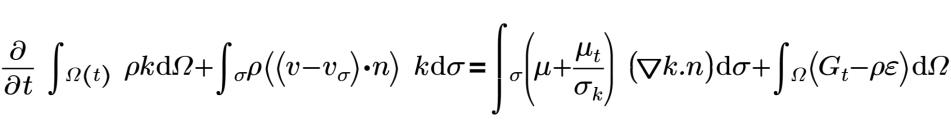
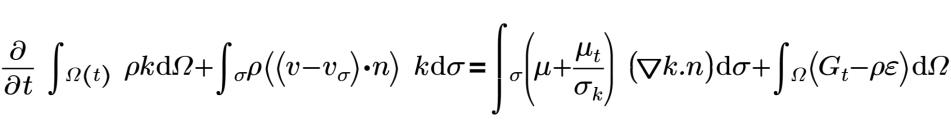
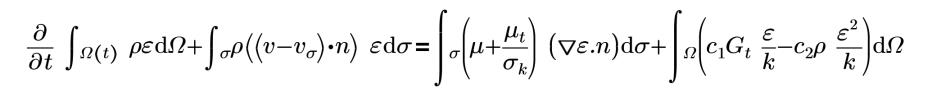
c1=1.44 | constants C1 |
c2=1.92 | constants C2 |
σk=1 | turbulence kinetic energy Prandtl number |
σz=1 | turbulence dissipation rate Prandtl number |
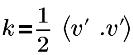 | turbulent kinetic energy |
v’ | turbulent fluctuation velocity |
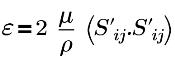 | turbulent energy dissipation rate |
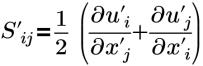 | strain tensor |
u’i(i=1,2,3) | components of the turbulent fluctuation velocity |
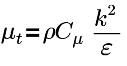 | turbulent viscosity, with Cμ=0.09 and E=9.793 |
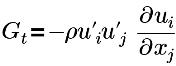 | turbulence generation term |
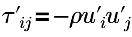 | turbulence Reynolds stress |
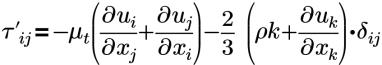 | the Boussinesq approximation to the Reynolds Stress |
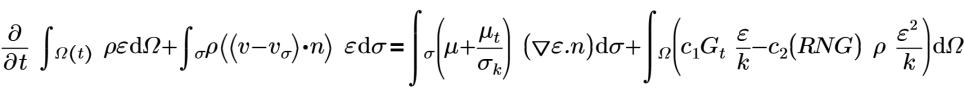
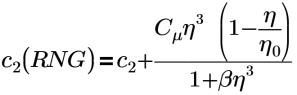
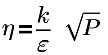
η0=4.38 | RNG constant (a hard-coded constant in Flow Analysis ) |
β=1.92 | RNG constant (a hard-coded constant in Flow Analysis ) |
P | local pressure |
c1=1.44 | constants C1 |
c2=1.92 | constants C2 |
σk=1 | turbulence kinetic energy Prandtl number |
σz=1 | turbulence dissipation rate Prandtl number |
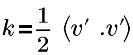 | turbulent kinetic energy |
v’ | turbulent fluctuation velocity |
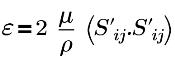 | turbulent energy dissipation rate |
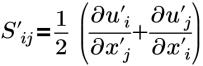 | strain tensor |
u’i(i=1,2,3) | components of the turbulent fluctuation velocity |
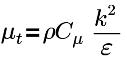 | turbulent viscosity, with Cμ=0.09 |
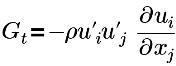 | turbulence generation term |
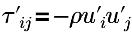 | turbulence Reynolds stress |
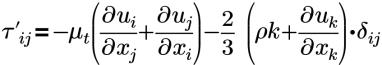 | Boussinesq approximation to the Reynolds stress |