Modeling of Cavitation Boundaries
In a cavitating flow, boundary conditions for the flow, energy, and turbulence modeling equations are the same as those in the single phase flows described in Flow, Heat and Turbulence modules. The boundary conditions for the transport equations consist of specified values and zero-gradient for the mass fractions of the vapor, noncondensable gas, and dissolved gas.
Inlet Boundary
Inlet mass fractions of vapor, noncondensable gas, and dissolved gas are all predetermined at an inlet boundary when the corresponding transport equations are solved:
• Vapor Mass Fraction—Should be specified at the inlet for all the model options since the vapor transport equation is always solved.
ƒv = ƒv,specified
• Gas Mass Fraction—Governing equation is solved in the variable gas fraction model or the full gas model. Therefore, the inlet value of ƒg is only required in these two model options:
ƒg = ƒg,specified
• Dissolved Gas Mass Fraction—Inlet condition is only required for the dissolved gas model. For the equilibrium dissolve gas model, the value is determined by the equilibrium condition.
ƒg,d = ƒg,d,specified
• Liquid Mass Fraction—Obtained by the physical constraint: ƒl = 1–ƒv–ƒg
For models in which the mass-fraction of the noncondensable gas is specified, ƒg is treated as a volume condition in Creo Flow Analysis.
Outlet/Symmetry/Wall Boundary
For all mass fraction transport equations solved in the cavitation models (vapor, gas, and dissolved gas), zero-gradient condition applies for all the outlet, symmetry, and wall boundaries, while the mass fraction for the liquid is obtained using the physical constraint:
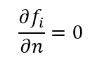
where i represents vapor, gas, and dissolved gas component, respectively.
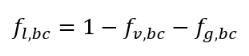
where bc is the outlet, symmetry, and wall boundary correspondingly.