벽 물리
벽의 로그 법칙:
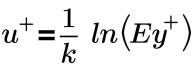
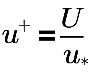
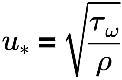
여기서 각 항목은 다음을 나타냅니다.
u+ | 치수부재 속도 |
U | 로컬(셀 중심) 속도 |
u* | 마찰 속도 |
τω | 벽 전단 |
ρ | 유체 속도 |
E | 상수 계수 |
k | 카르만 상수(0.41) |
y+ | 비치수 벽-셀 거리 |
벽 함수 및 법칙
벽 함수는 슬립이 없는 경계(벽)에서 매우 조밀한 격자선 분포가 없는 경우 터뷸런스 경계 레이어의 벽 근처 동작을 모델링하는 데 필요합니다. 문헌에는 매우 다양한 벽 함수가 존재하며, 특정 응용 프로그램에 적합한 함수를 찾아보는 것이 좋습니다. 벽 함수의 사용에는 경계 레이어 이론 Schlichting (Boundary Layer Theory, 6th Edition, 1968 ISBN 07-055329-7)이 적용됩니다.
벽에서 인접 흐름의 지점까지의 비치수 거리 y+는 다음과 같이 정의됩니다.
여기서 각 항목은 다음을 나타냅니다.
마찰 속도 | |
v | 동적 점도 |
• 점성 서브레이어 0 < y+< 5
• 버퍼 레이어 5 < y+< 30
• 관성 레이어 30 < y+< 200
다음에 설명된 터뷸런스 점도 모델을 지원하기 위해 개발된 몇 가지 벽 함수가 있습니다.
• 표준 - Launder와 Spalding이 제안한 것으로 벽 근처의 터뷸런스 평균 속도 프로파일을 정의합니다. 표준 벽 함수를 사용하는 평균 속도 분포의 벽 법칙 공식은 다음과 같이 표현됩니다.
관성 서브레이어 및 점성 서브레이어에서:
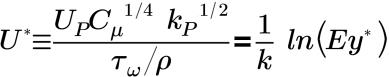
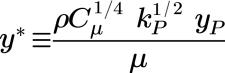
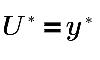
여기서 각 항목은 다음을 나타냅니다.
k=0.4187 | 카르만 상수 |
E=9.793 | 경험적 상수 |
UP | P 지점에서 유체의 평균 속도 |
kP | P 지점에서 터뷸런스 운동 에너지 |
yP | P 지점에서 벽까지의 거리 |
μ | 유체의 역학 점도 |
표준 벽 함수는 산업용 응용 프로그램에서 사용되며, 유체 흐름에 대한 문서에도 설명되어 있습니다. 이는 터뷸런스 운동 에너지 생산 K와 터뷸런스 에너지 소산율이 로컬로 평형 상태라는 가정 하에 파생되었습니다. 표준 벽 함수는 기압 경도가 작고, 분리가 없고, 재순환이 없고, 가속 또는 감속 효과가 미미한 흐름을 예측할 때 가장 정확합니다.
• Nonequilibrium(Kim) - Kim이 제안한 것으로 벽 근처의 터뷸런스 평균 속도 프로파일을 정의합니다. Nonequilibrium(Kim) 벽 함수를 사용하는 평균 속도 분포의 벽 법칙 공식은 다음과 같이 표현됩니다.
관성 서브레이어에서:
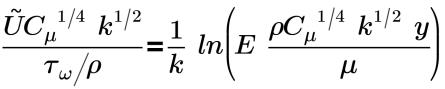
k=0.4187 | 카르만 상수 |
E=9.793 | 경험적 상수 |
UP | P 지점에서 유체의 평균 속도 |
kP | P 지점에서 유체의 터뷸런스 운동 에너지 평균 속도 |
yP | P 지점부터 P 지점에서 유체의 벽 터뷸런스 운동 에너지 평균 속도까지의 거리 |
μ | P 지점에서 유체의 터뷸런스 운동 에너지 평균 속도에 대한 유체의 역학 점도 |
Cμ | 0.09 |
Nonequilibrium(Kim) 벽 함수는 터뷸런스 운동 에너지 생산이 소산율과 같지 않다고 가정합니다. Nonequilibrium(Kim) 벽 함수는 기압 경도 효과를 고려합니다. 이 함수는 점성 서브레이어와 완전 터뷸런스 관성 레이어의 처리에 대해 2단 레이어 모델을 사용합니다. Nonequilibrium(Kim) 벽 함수는 점성 서브레이어의 선형 법칙과 관성 서브레이어의 로그 법칙 간에 원활한 전환을 위해 벽 버퍼 영역(3 < y+ < 10)에서 블렌딩 함수를 사용하는 개선된 벽 처리를 사용합니다.
• 통합(Shih) - Shih가 제안한 것으로 경계 레이어에 대한 터뷸런스 평균 속도 프로파일을 정의합니다. 통합(Shih) 벽 함수를 사용하는 평균 속도 분포의 벽 법칙 공식은 다음과 같이 표현됩니다.
f1(Yτ+) 및 f2(Yρ+)가 점진적 적합식인 전체 경계 레이어에 대해:
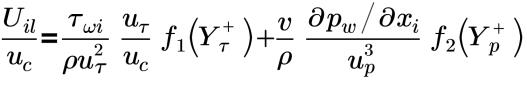
통합(Shih) 벽 함수는 점성 서브레이어, 버퍼 레이어 및 관성 레이어에 유효합니다(통합). 통합(Shih) 벽 함수는 순압력 및 역압력 경도가 모두 있는 흐름과 가속, 감속 및 재순환이 있는 벽 경계의 복잡한 흐름에 대해 적합합니다. 이 벽 함수는 점성 서브레이어, 버퍼 레이어 및 관성 서브레이어의 처리에 3단 모델을 사용합니다.
벽 미세도 모델
벽 미세도 모델(Wall Roughness Model)은 벽의 서피스 마무리에 대한 미세도(미터)를 나타냅니다.
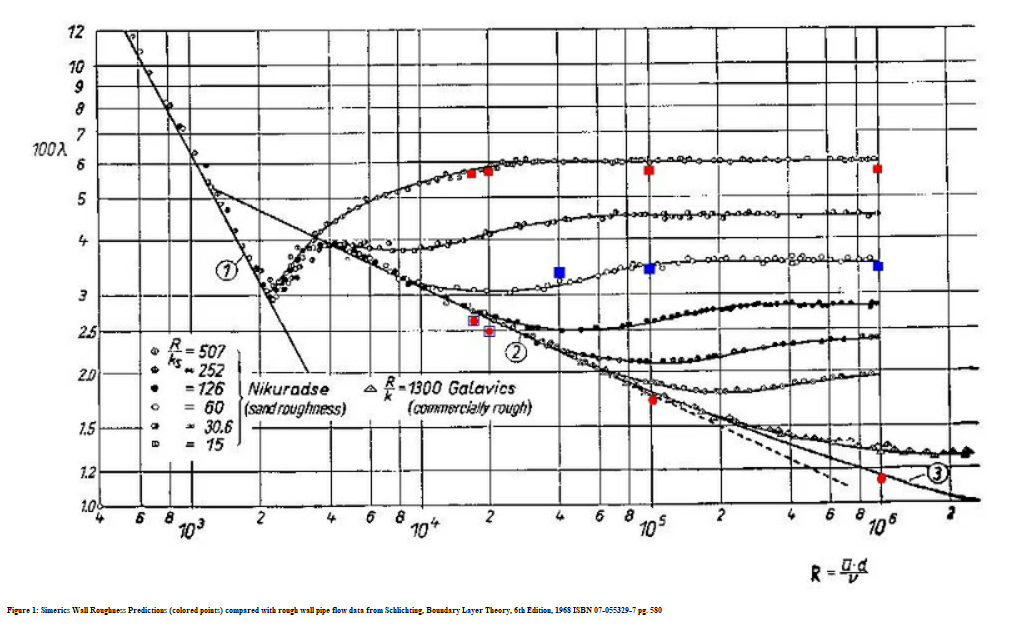
거친 벽 파이프 흐름 데이터와 비교한 Creo Flow Analysis 벽 미세도 예측(색상 점) Schlichting, Boundary Layer Theory, 6th Edition, 1968 ISBN 07-055329-7 pg. 580.