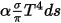방사 열 전달 모델링
열 유체 시스템에서 솔리드 서피스 및/또는 유체 흐름은 방사를 통해 가열 또는 냉각될 수 있습니다. CFA 모델에서 방사 열 전달은 방사 전달 방정식(RTE)을 푼 다음 총 에너지 보존 방정식에 대한 방사 소스 항을 구하는 방법으로 설명됩니다. 널리 사용되는 모델링 방식인 서피스-서피스(S2S) 방사 모델은 Creo Flow Analysis에서 선택한 모델입니다.
방사 전달 방정식
방사선은 흡수, 방출 및 산란 매체 레이어를 특정 방향으로 트래버스하므로 광선이 흡수 및 산란을 통해 광선으로부터의 에너지를 잃습니다. 또한 광선은 광선으로 직접 향하는 방출 및 산란을 통해 매체의 광원으로부터 에너지를 얻습니다. 매체의 무한 레이어에서 광선의 전체적인 에너지 균형은 방사 전송 방정식(RTE)이라고 하는 미분 방정식을 생성합니다.
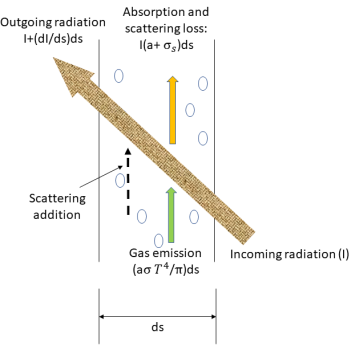
방사 전송 방정식을 파생하기 위해 그림에 표시된 것처럼 강도가 I인 방사선의 입사 광선이 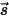 의 방향으로 증분 두께가 ds인 매체(예: 가스)를 통과하여 이동하는 것으로 간주합니다. 매체 레이어를 통과하여 위치
의 방향으로 증분 두께가 ds인 매체(예: 가스)를 통과하여 이동하는 것으로 간주합니다. 매체 레이어를 통과하여 위치 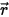 및
및 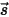 방향으로 입사한 경우 방사 강도
방향으로 입사한 경우 방사 강도 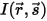 를 증가(에너지 증가 +) 또는 감소(에너지 손실 -)하는 4가지 방식으로 변화합니다.
를 증가(에너지 증가 +) 또는 감소(에너지 손실 -)하는 4가지 방식으로 변화합니다.
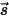 의 방향으로 증분 두께가 ds인 매체(예: 가스)를 통과하여 이동하는 것으로 간주합니다. 매체 레이어를 통과하여 위치
의 방향으로 증분 두께가 ds인 매체(예: 가스)를 통과하여 이동하는 것으로 간주합니다. 매체 레이어를 통과하여 위치 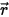 및
및 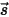 방향으로 입사한 경우 방사 강도
방향으로 입사한 경우 방사 강도 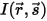 를 증가(에너지 증가 +) 또는 감소(에너지 손실 -)하는 4가지 방식으로 변화합니다.
를 증가(에너지 증가 +) 또는 감소(에너지 손실 -)하는 4가지 방식으로 변화합니다.• 흡수 - 매체(예: 가스)는 해당 매체를 트래버스하는 방사의 일부를 흡수합니다. 흡수 계수 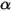 를 사용하는 경우 흡수를 통해 손실된 방사 에너지는 다음과 같습니다.
를 사용하는 경우 흡수를 통해 손실된 방사 에너지는 다음과 같습니다.
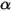 를 사용하는 경우 흡수를 통해 손실된 방사 에너지는 다음과 같습니다.
를 사용하는 경우 흡수를 통해 손실된 방사 에너지는 다음과 같습니다.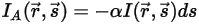
방정식 2.282
• 산란 - 광선이 매체를 트래버스하는 경우 매체(예: 기체)는 방사 에너지의 일부를 다른 방향(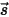 방향에서 벗어나)으로 산란합니다. 분산 계수
방향에서 벗어나)으로 산란합니다. 분산 계수 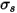 를 사용할 경우 분산을 통해 손실된 방사 에너지는 다음과 같습니다.
를 사용할 경우 분산을 통해 손실된 방사 에너지는 다음과 같습니다.
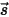 방향에서 벗어나)으로 산란합니다. 분산 계수
방향에서 벗어나)으로 산란합니다. 분산 계수 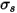 를 사용할 경우 분산을 통해 손실된 방사 에너지는 다음과 같습니다.
를 사용할 경우 분산을 통해 손실된 방사 에너지는 다음과 같습니다.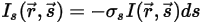
방정식 2.283
또한 n이 매체의 굴절률(진공에서의 빛의 속도와 특정 매체에서의 속도 비율로 정의됨)이라고 가정하면, 방사선에 의해 얻은 실제 에너지는 다음과 같습니다.
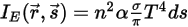
방정식 2.284
• 다른 방사 분산 - 매체 레이어 내의 다른 방사 소스의 일부는 위치 및 방향 벡터 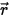 및
및 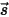 에 의존하는 방사선으로 산란됩니다.
에 의존하는 방사선으로 산란됩니다. 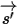
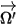 를 사용하여 방사 빔의 방향과 솔리드 각도를 나타내고
를 사용하여 방사 빔의 방향과 솔리드 각도를 나타내고 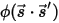 를 위상 함수로 사용하면 광선 강도의 일부가
를 위상 함수로 사용하면 광선 강도의 일부가 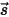 의 방향으로 산란하기 위해 모든 방향으로 이동합니다.
의 방향으로 산란하기 위해 모든 방향으로 이동합니다.
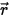 및
및 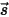 에 의존하는 방사선으로 산란됩니다.
에 의존하는 방사선으로 산란됩니다. 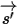
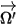 를 사용하여 방사 빔의 방향과 솔리드 각도를 나타내고
를 사용하여 방사 빔의 방향과 솔리드 각도를 나타내고 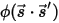 를 위상 함수로 사용하면 광선 강도의 일부가
를 위상 함수로 사용하면 광선 강도의 일부가 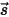 의 방향으로 산란하기 위해 모든 방향으로 이동합니다.
의 방향으로 산란하기 위해 모든 방향으로 이동합니다.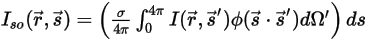
방정식 2.285
방정식 2.285에서 산란 프로세스는 무시됩니다.
들어오는 방사가 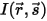 이고, 나가는 방사가
이고, 나가는 방사가 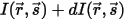 인 경우
인 경우 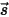 방향에서의 방사 에너지 균형은 다음과 같습니다.
방향에서의 방사 에너지 균형은 다음과 같습니다.
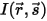 이고, 나가는 방사가
이고, 나가는 방사가 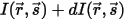 인 경우
인 경우 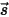 방향에서의 방사 에너지 균형은 다음과 같습니다.
방향에서의 방사 에너지 균형은 다음과 같습니다.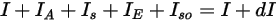
방정식 2.286
방정식 2.282에서 방정식 2.285를 방정식 2.286로 대체하고 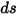 로 나누면 방사 전송 방정식(RTE)이 다음과 같이 나타납니다.
로 나누면 방사 전송 방정식(RTE)이 다음과 같이 나타납니다.
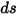 로 나누면 방사 전송 방정식(RTE)이 다음과 같이 나타납니다.
로 나누면 방사 전송 방정식(RTE)이 다음과 같이 나타납니다.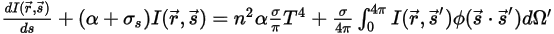
방정식 2.287
RTE는 고정 방향 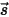 의 방사 강도
의 방사 강도 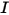 에 대한 1차 미적분 방정식입니다. 도메인 내에서 이 방정식을 풀려면 도메인 내의 온도 필드가 필요하며 내부 및 외부 서피스 모두의
에 대한 1차 미적분 방정식입니다. 도메인 내에서 이 방정식을 풀려면 도메인 내의 온도 필드가 필요하며 내부 및 외부 서피스 모두의 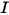 에 대한 경계 조건과 서로 다른 두 매체 간의 인터페이스도 필요합니다.
에 대한 경계 조건과 서로 다른 두 매체 간의 인터페이스도 필요합니다.
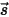 의 방사 강도
의 방사 강도 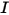 에 대한 1차 미적분 방정식입니다. 도메인 내에서 이 방정식을 풀려면 도메인 내의 온도 필드가 필요하며 내부 및 외부 서피스 모두의
에 대한 1차 미적분 방정식입니다. 도메인 내에서 이 방정식을 풀려면 도메인 내의 온도 필드가 필요하며 내부 및 외부 서피스 모두의 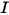 에 대한 경계 조건과 서로 다른 두 매체 간의 인터페이스도 필요합니다.
에 대한 경계 조건과 서로 다른 두 매체 간의 인터페이스도 필요합니다.로컬 매체 온도는 열 모듈에 설명된 전체 에너지(방사 소스 포함) 보존 방정식을 풀어서 구합니다. 그러나 열 방사의 경우 경계 처리가 복잡하며 방사 모델에 따라 달라집니다. 일반적으로 경계는 방출, 반사 및 흡수하는 불투명 매체일 수 있으며 경계는 전송하는 반투명 매체일 수도 있습니다. 반사 및 전송은 확산 및/또는 확산될 수 있습니다. 예를 들어 회색 방사를 방출 및 반사하는 불투명 경계에서, 그리고 반사 유형에 따라 광선의 강도는 다음과 같이 표현할 수 있습니다.
◦ 확산 방출 및 반사가 있는 불투명 경계:
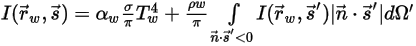
방정식 2.288
◦ 확산 방출 및 거울반사가 있는 불투명 경계:
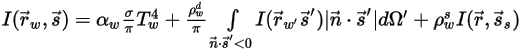
방정식 2.289
여기서 각 항목은 다음을 나타냅니다.
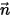 ⃗ ⃗ | 위치 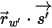 에서 직각-서피스 단위 벡터 에서 직각-서피스 단위 벡터 |
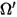 | 확산 반사광의 방향 및 솔리드 각도(모든 방향으로의 균일한 반사) |
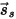 | 거울 반사광의 방향(입사에 따라 완전 반사) |
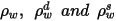 | 각각 서피스 반사광, 확산 반사광 및 거울반사광을 나타내며 관계는 다음과 같습니다. 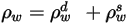 방정식 2.290 |
지정된 경계 조건에서 방정식 2.287은 특정 방향으로의 방사 강도 전송을 제어합니다. 회색 방사의 경우 방정식 2.287은 구 내의 다른 모든 방향으로 해결되어야 합니다. 비 회색 방사의 경우 강도는 또한 파장에 따라서도 달라집니다. 따라서 파장의 전체 스펙트럼에서 모든 방향으로 해결되어야 합니다. 방사 전달 방정식을 직접 해결하려면 시간이 많이 소요됩니다. 따라서 대부분의 엔지니어링 시뮬레이션에서는 방향 및 스펙트럼 종속성을 고려하는 다소 단순화된 모델을 사용하는 것이 좋습니다. CFD 시뮬레이션에서는 참조에서 세부 설명을 찾을 수 있는 다음과 같은 방사 모델이 정기적으로 채택됩니다.
참고 문헌: R. Siegel and J. R. Howell, Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ 로슬랜드 방사 모델
참고 문헌: R, Siegel and J. R. Howell, Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ P-1 방사 모델
참고 문헌: R. Siegel and J. R. Howell, Thermal Radiation Heat Transfer, Hemisphere Publishing Corporation, Washington DC, 1992.
▪ 불연속 전달 방사 모델
참고 문헌: N. G. Shah, A New Method of Computation of Radiant Heat Transfer in Combustion Chambers", PhD thesis, Imperial College of Science and Technology, London, England, 1979.
참고 문헌: M. G. Carvalho, T. Farias, and P. Fontes, Predicting Radiative Heat Transfer in Absorbing, Emitting, and Scattering Media Using the Discrete Transfer Method", In W. A. Fiveland et al., editor, Fundamentals of Radiation Heat Transfer, volume 160, pages 17-26. ASME HTD, 1991.
▪ 서피스-서피스(S2S) 방사 모델
참고 문헌: R. Siegel and J. R. Howell, Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ 불연속 좌표(DO) 방사 모델
참고 문헌: G. D. Raithby and E. H. Chui, A Finite-Volume Method for Predicting a Radiant Heat Transfer in Enclosures with Participating Media", J. Heat Transfer, 112:415-423, 1990.
참고 문헌: E. H. Chui and G. D. Raithby, Computation of Radiant Heat Transfer on a Non-Orthogonal Mesh Using the Finite-Volume Method”, Numerical Heat Transfer, Part B, 23:269-288, 1993.
각 모델에는 정밀도와 비용에 관한 고유한 장점과 제한이 있습니다. 예를 들어, 로슬랜드 모델은 입사 방사에 대한 전송 방정식을 풀지 않습니다. 이 모델은 가장 빠른 방사 모델이며 필요한 추가 메모리가 가장 적습니다. 로슬랜드는 방사 전송 방정식의 지나친 단순화로 인해 광학적으로 두꺼운(광학 두께는 매체에서 전송된 방사력에 대한 입사 비율의 자연 로그) 매체에만 사용할 수 있습니다.
불연속 좌표(DO) 방사 모델은 방정식 2.287을 공간 좌표 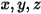 의 방사 강도에 대한 전송 방정식으로 변환하고 벡터 방향
의 방사 강도에 대한 전송 방정식으로 변환하고 벡터 방향 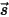 과 관련된 유한 개수의 불연속 솔리드 각도를 통해 이를 해결합니다. 선택한 솔리드 각도의 수에 따라 정밀도와 계산 비용이 직접 결정됩니다. DO 모델링 접근법은 유체 흐름 및 에너지 방정식에 사용된 접근법과 동일합니다. 현재는 광학 두께의 전체 범위에 걸쳐 있는 가장 일반적인 방사 모델이며 서피스-서피스 방사부터 연소 시스템과 같은 참여 방사에 이르는 문제에 적용될 수 있습니다. 그러나 비회색 방사의 경우 DO 모델의 계산 비용이 높습니다.
과 관련된 유한 개수의 불연속 솔리드 각도를 통해 이를 해결합니다. 선택한 솔리드 각도의 수에 따라 정밀도와 계산 비용이 직접 결정됩니다. DO 모델링 접근법은 유체 흐름 및 에너지 방정식에 사용된 접근법과 동일합니다. 현재는 광학 두께의 전체 범위에 걸쳐 있는 가장 일반적인 방사 모델이며 서피스-서피스 방사부터 연소 시스템과 같은 참여 방사에 이르는 문제에 적용될 수 있습니다. 그러나 비회색 방사의 경우 DO 모델의 계산 비용이 높습니다.
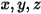 의 방사 강도에 대한 전송 방정식으로 변환하고 벡터 방향
의 방사 강도에 대한 전송 방정식으로 변환하고 벡터 방향 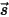 과 관련된 유한 개수의 불연속 솔리드 각도를 통해 이를 해결합니다. 선택한 솔리드 각도의 수에 따라 정밀도와 계산 비용이 직접 결정됩니다. DO 모델링 접근법은 유체 흐름 및 에너지 방정식에 사용된 접근법과 동일합니다. 현재는 광학 두께의 전체 범위에 걸쳐 있는 가장 일반적인 방사 모델이며 서피스-서피스 방사부터 연소 시스템과 같은 참여 방사에 이르는 문제에 적용될 수 있습니다. 그러나 비회색 방사의 경우 DO 모델의 계산 비용이 높습니다.
과 관련된 유한 개수의 불연속 솔리드 각도를 통해 이를 해결합니다. 선택한 솔리드 각도의 수에 따라 정밀도와 계산 비용이 직접 결정됩니다. DO 모델링 접근법은 유체 흐름 및 에너지 방정식에 사용된 접근법과 동일합니다. 현재는 광학 두께의 전체 범위에 걸쳐 있는 가장 일반적인 방사 모델이며 서피스-서피스 방사부터 연소 시스템과 같은 참여 방사에 이르는 문제에 적용될 수 있습니다. 그러나 비회색 방사의 경우 DO 모델의 계산 비용이 높습니다.위에서 언급한 방사 모델 중 서피스-서피스(S2S) 방사 모델은 참여 매체를 고려하지 않고 엔클로저 방사 전달을 모델링할 때 특히 유용합니다. 일반적인 예로는 방사 공간 히터와, 자동차 언더후드 및 언더바디 시스템이 있습니다. 이러한 경우에는 참여 방사에 대한 방사 모델이 효율적이지 않을 수 있습니다. DO 방사 모델에 비해 S2S 모델은 보기 계수 계산 자체가 CPU 집약적일 수는 있지만 이터레이션당 시간이 더 빠릅니다. Creo Flow Analysis에서 현재 선택된 방사 열 전달 모델은 S2S 방사 모델입니다.
서피스-서피스(S2S) 방사 모델
서피스-서피스 방사 모델은 참여 매체 없는 회색 확산 서피스의 엔클로저에서 방사 교환을 설명합니다. 서피스-서피스 방사 에너지 교환은 두 가지 주요 계수에 의존합니다. 관련된 서피스의 방사 특성과 표면적 및 형태를 포함한 형상 매개 변수, 그리고 다른 분리 거리 및 방향에 도달하는 상대적인 위치입니다. S2S 방사 모델에서 서피스 방사 열 전달은 회색 확산 방사 모델에 의해 고려되며 형상 매개 변수는 보기 계수라는 형상 함수로 계산됩니다.
• 회색 확산 방사
S2S 방사 모델은 서피스가 회색이고 확산(회색 방사)된다고 가정합니다. 회색 서피스의 경우 서피스의 방사율(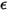 )과 흡수율(
)과 흡수율(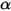 )은 모두 들어오고 나가는 광선의 파장과 무관합니다. 키르히호프의 열 방사 법칙에 따르면 방정식 2.274에서 방사율은 흡수율과 같습니다.
)은 모두 들어오고 나가는 광선의 파장과 무관합니다. 키르히호프의 열 방사 법칙에 따르면 방정식 2.274에서 방사율은 흡수율과 같습니다.
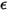 )과 흡수율(
)과 흡수율(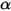 )은 모두 들어오고 나가는 광선의 파장과 무관합니다. 키르히호프의 열 방사 법칙에 따르면 방정식 2.274에서 방사율은 흡수율과 같습니다.
)은 모두 들어오고 나가는 광선의 파장과 무관합니다. 키르히호프의 열 방사 법칙에 따르면 방정식 2.274에서 방사율은 흡수율과 같습니다.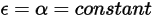
방정식 2.291
또한 확산 서피스를 가정한 경우 서피스에서 반사가 발생하지 않으며 서피스 입사 방사의 반사율(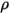 )은 솔리드 각도에 대해 등방성입니다. 방정식 2.290에서 서피스 반사는 다음과 같이 결정됩니다.
)은 솔리드 각도에 대해 등방성입니다. 방정식 2.290에서 서피스 반사는 다음과 같이 결정됩니다.
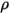 )은 솔리드 각도에 대해 등방성입니다. 방정식 2.290에서 서피스 반사는 다음과 같이 결정됩니다.
)은 솔리드 각도에 대해 등방성입니다. 방정식 2.290에서 서피스 반사는 다음과 같이 결정됩니다.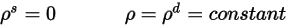
방정식 2.292
여기서 각 항목은 다음을 나타냅니다.
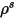 | 서피스 반사 |
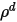 | 확산 반사광 |
불투명 또는 반투명 서피스의 경우 투과율 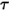 도 파장과 무관합니다.
도 파장과 무관합니다.
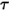 도 파장과 무관합니다.
도 파장과 무관합니다.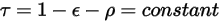
방정식 2.293
회색 확산 서피스-서피스 모델은 서피스 간의 방사 에너지 교환이 해당 서피스를 분리하는 매체에 의해 실질적으로 영향을 받지 않는다고 가정합니다. 따라서 서피스에 대해 단위 면적(복사조도)당 특정 양의 방사 에너지 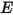 가 입사되는 경우 반사, 흡수 및 전달되는 방사 에너지의 부분은 각각
가 입사되는 경우 반사, 흡수 및 전달되는 방사 에너지의 부분은 각각 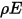 ,
, 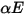 및
및 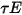 입니다. 대부분의 응용 프로그램에서 서피스는 적외선 스펙트럼의 열 방사에 불투명하므로 방사 서피스를 더 불투명한 것으로 간주할 수 있습니다. 따라서 투과율
입니다. 대부분의 응용 프로그램에서 서피스는 적외선 스펙트럼의 열 방사에 불투명하므로 방사 서피스를 더 불투명한 것으로 간주할 수 있습니다. 따라서 투과율 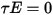 은 무시할 수 있습니다. 방정식 2.273 및 방정식 2.274에서 서피스 반사율
은 무시할 수 있습니다. 방정식 2.273 및 방정식 2.274에서 서피스 반사율 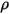 은 다음과 같이 표현됩니다.
은 다음과 같이 표현됩니다.
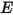 가 입사되는 경우 반사, 흡수 및 전달되는 방사 에너지의 부분은 각각
가 입사되는 경우 반사, 흡수 및 전달되는 방사 에너지의 부분은 각각 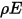 ,
, 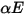 및
및 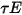 입니다. 대부분의 응용 프로그램에서 서피스는 적외선 스펙트럼의 열 방사에 불투명하므로 방사 서피스를 더 불투명한 것으로 간주할 수 있습니다. 따라서 투과율
입니다. 대부분의 응용 프로그램에서 서피스는 적외선 스펙트럼의 열 방사에 불투명하므로 방사 서피스를 더 불투명한 것으로 간주할 수 있습니다. 따라서 투과율 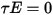 은 무시할 수 있습니다. 방정식 2.273 및 방정식 2.274에서 서피스 반사율
은 무시할 수 있습니다. 방정식 2.273 및 방정식 2.274에서 서피스 반사율 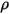 은 다음과 같이 표현됩니다.
은 다음과 같이 표현됩니다.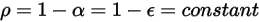
방정식 2.294
서피스 회색 확산 방사의 가정을 통해 S2S 모델링 방정식은 각 서피스의 에너지 보존을 기반으로 구성됩니다.
• S2S 모델링 방정식
S2S 모델의 주요 가정은 폐쇄형 시스템에서 방사 열 전달이 회색 확산 서피스(회색 방사) 사이에서만 발생한다는 것입니다. 서피스를 분리하는 매체에서 방사선 흡수, 방출 또는 산란을 무시할 수 있습니다. 따라서 수치 분석을 위해 서피스-서피스 방사만 고려하십시오.
지정된 서피스를 나가는 방사 에너지 흐름은 직접 방출되고 반사된 에너지로 구성됩니다. 반사된 에너지 흐름은 주변으로부터의 입사 에너지 흐름에 의존하며, 이는 다른 모든 서피스를 떠나는 에너지 흐름의 관점에서 표현될 수 있습니다. 서피스에 대한 순 방사 에너지 흐름을 계산하려면 라디오시티 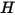 를 정의하는 것이 편리합니다. 라디오시티는 단위 면적당 방사율(방사도)
를 정의하는 것이 편리합니다. 라디오시티는 단위 면적당 방사율(방사도) 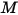 과 단위 면적당 서피스에 의해 수신된 방사 전력의 반사된 부분(복사조도)
과 단위 면적당 서피스에 의해 수신된 방사 전력의 반사된 부분(복사조도) 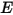 의 합계입니다.
의 합계입니다.
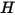 를 정의하는 것이 편리합니다. 라디오시티는 단위 면적당 방사율(방사도)
를 정의하는 것이 편리합니다. 라디오시티는 단위 면적당 방사율(방사도) 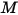 과 단위 면적당 서피스에 의해 수신된 방사 전력의 반사된 부분(복사조도)
과 단위 면적당 서피스에 의해 수신된 방사 전력의 반사된 부분(복사조도) 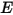 의 합계입니다.
의 합계입니다.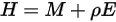
방정식 2.295
불투명 서피스 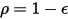 의 경우 라디오시티는 다음과 같습니다.
의 경우 라디오시티는 다음과 같습니다.
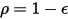 의 경우 라디오시티는 다음과 같습니다.
의 경우 라디오시티는 다음과 같습니다.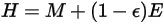
방정식 2.296
따라서 S2S 모델에서의 가정에 따라 다음 선형 연립 방정식을 공식화하여 폐쇄된 시스템의 각 서피스에 대한 라디오시티를 계산할 수 있습니다. 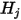 가 임의의 서피스
가 임의의 서피스 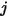 에 대한 라디오시티이고,
에 대한 라디오시티이고, 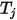 는 서피스 온도,
는 서피스 온도, 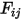 가 서피스
가 서피스 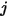 및
및  사이의 보기 계수라고 가정할 때, 라디오시티는 서피스
사이의 보기 계수라고 가정할 때, 라디오시티는 서피스  에 있습니다.
에 있습니다.
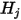 가 임의의 서피스
가 임의의 서피스 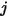 에 대한 라디오시티이고,
에 대한 라디오시티이고, 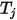 는 서피스 온도,
는 서피스 온도, 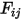 가 서피스
가 서피스 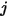 및
및  사이의 보기 계수라고 가정할 때, 라디오시티는 서피스
사이의 보기 계수라고 가정할 때, 라디오시티는 서피스  에 있습니다.
에 있습니다.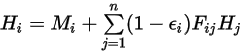
방정식 2.297
여기서 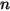 은 방사 열 전달에 참여되는 서피스 번호입니다. 크로네커 기호
은 방사 열 전달에 참여되는 서피스 번호입니다. 크로네커 기호 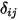 를 도입하고 회색 방사에 대한 슈테판-볼츠만의 법칙, 방정식 2.278을 적용하면 방정식 2.297을 재조정하고 S2S 모델링 방정식을 유도할 수 있습니다.
를 도입하고 회색 방사에 대한 슈테판-볼츠만의 법칙, 방정식 2.278을 적용하면 방정식 2.297을 재조정하고 S2S 모델링 방정식을 유도할 수 있습니다.
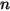 은 방사 열 전달에 참여되는 서피스 번호입니다. 크로네커 기호
은 방사 열 전달에 참여되는 서피스 번호입니다. 크로네커 기호 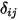 를 도입하고 회색 방사에 대한 슈테판-볼츠만의 법칙, 방정식 2.278을 적용하면 방정식 2.297을 재조정하고 S2S 모델링 방정식을 유도할 수 있습니다.
를 도입하고 회색 방사에 대한 슈테판-볼츠만의 법칙, 방정식 2.278을 적용하면 방정식 2.297을 재조정하고 S2S 모델링 방정식을 유도할 수 있습니다.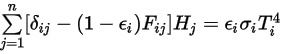
방정식 2.298
미리 계산된 보기 계수 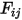 를 사용하여 선형 연립 방정식인 방정식 2.298을 풀면 관련 서피스에 대해
를 사용하여 선형 연립 방정식인 방정식 2.298을 풀면 관련 서피스에 대해 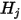 를 구할 수 있습니다. 그러면 각 서피스의 방사 순 전열이 쉽게 계산됩니다. 서피스
를 구할 수 있습니다. 그러면 각 서피스의 방사 순 전열이 쉽게 계산됩니다. 서피스  의 경우 순 방사 열류
의 경우 순 방사 열류 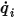 는 단위 면적당 나가는 방사(
는 단위 면적당 나가는 방사(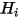 )와 들어오는 방사(
)와 들어오는 방사(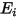 ) 간의 차이입니다. 방정식 2.278 및 방정식 2.296에서 다음과 같은 흐름 공식을 파생할 수 있습니다.
) 간의 차이입니다. 방정식 2.278 및 방정식 2.296에서 다음과 같은 흐름 공식을 파생할 수 있습니다.
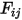 를 사용하여 선형 연립 방정식인 방정식 2.298을 풀면 관련 서피스에 대해
를 사용하여 선형 연립 방정식인 방정식 2.298을 풀면 관련 서피스에 대해 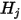 를 구할 수 있습니다. 그러면 각 서피스의 방사 순 전열이 쉽게 계산됩니다. 서피스
를 구할 수 있습니다. 그러면 각 서피스의 방사 순 전열이 쉽게 계산됩니다. 서피스  의 경우 순 방사 열류
의 경우 순 방사 열류 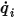 는 단위 면적당 나가는 방사(
는 단위 면적당 나가는 방사(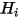 )와 들어오는 방사(
)와 들어오는 방사(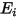 ) 간의 차이입니다. 방정식 2.278 및 방정식 2.296에서 다음과 같은 흐름 공식을 파생할 수 있습니다.
) 간의 차이입니다. 방정식 2.278 및 방정식 2.296에서 다음과 같은 흐름 공식을 파생할 수 있습니다.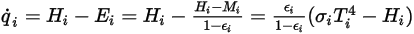
방정식 2.299
지정된 표면적 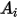 의 경우 서피스를 나가는 순 방사 전열
의 경우 서피스를 나가는 순 방사 전열 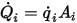 은 다음과 같이 계산됩니다.
은 다음과 같이 계산됩니다.
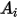 의 경우 서피스를 나가는 순 방사 전열
의 경우 서피스를 나가는 순 방사 전열 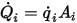 은 다음과 같이 계산됩니다.
은 다음과 같이 계산됩니다.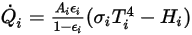
방정식 2.300
S2S 모델은 방정식 2.298 형태의 선형 연립 방정식으로 구성됩니다. 모델 응용 프로그램의 장점은 지정된 보기 계수와 온도에 대해 수치 알고리즘을 적용하여 계산되는 선형 연립 방정식을 풀어 순 전열을 계산하는 것입니다. 그러나 제안된 서피스-서피스 모델을 적용하는 데 있어 가장 큰 어려움은 n개의 관련 서피스에 대한 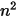 보기 계수의 계산입니다. 특히 서피스 수가 증가하면서 시간이 많이 소요될 수 있습니다.
보기 계수의 계산입니다. 특히 서피스 수가 증가하면서 시간이 많이 소요될 수 있습니다.
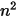 보기 계수의 계산입니다. 특히 서피스 수가 증가하면서 시간이 많이 소요될 수 있습니다.
보기 계수의 계산입니다. 특히 서피스 수가 증가하면서 시간이 많이 소요될 수 있습니다.보기 계수 계산
S2S 모델링 방정식 2.298에서 보기 계수 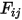 는 서피스
는 서피스  를 떠난 방사와 서피스
를 떠난 방사와 서피스 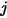 에 도달한 방사의 비율입니다. 그림 2.37에서 볼 수 있는 것처럼
에 도달한 방사의 비율입니다. 그림 2.37에서 볼 수 있는 것처럼 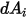 가 서피스
가 서피스  의 미분 영역이고,
의 미분 영역이고, 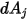 가 서피스
가 서피스 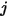 의 미분 영역이며,
의 미분 영역이며, 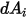 와
와 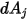 사이의 거리가
사이의 거리가 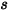 라고 가정할 때, 보기 계수
라고 가정할 때, 보기 계수 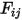 는 다음과 같이
는 다음과 같이 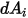 에서
에서 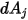 까지의 거리
까지의 거리 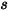 로 표현합니다.
로 표현합니다.
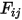 는 서피스
는 서피스  를 떠난 방사와 서피스
를 떠난 방사와 서피스 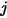 에 도달한 방사의 비율입니다. 그림 2.37에서 볼 수 있는 것처럼
에 도달한 방사의 비율입니다. 그림 2.37에서 볼 수 있는 것처럼 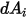 가 서피스
가 서피스  의 미분 영역이고,
의 미분 영역이고, 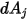 가 서피스
가 서피스 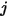 의 미분 영역이며,
의 미분 영역이며, 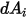 와
와 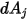 사이의 거리가
사이의 거리가 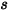 라고 가정할 때, 보기 계수
라고 가정할 때, 보기 계수 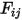 는 다음과 같이
는 다음과 같이 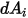 에서
에서 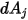 까지의 거리
까지의 거리 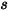 로 표현합니다.
로 표현합니다.
방정식 2.301
여기서 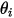 및
및 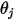 는 서피스 수직 방향과 두 개의 미분 영역 사이의 광선 각도입니다.
는 서피스 수직 방향과 두 개의 미분 영역 사이의 광선 각도입니다.
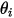 및
및 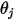 는 서피스 수직 방향과 두 개의 미분 영역 사이의 광선 각도입니다.
는 서피스 수직 방향과 두 개의 미분 영역 사이의 광선 각도입니다.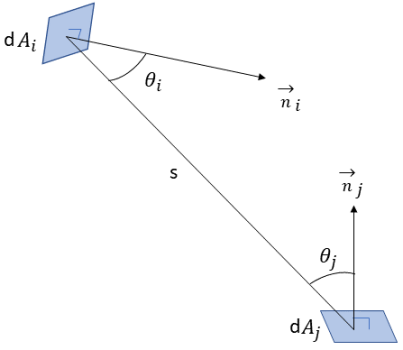
그림 2.37
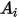 및
및 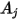 가 각각
가 각각  및
및 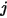 서피스의 지정된 영역인 경우, 서피스
서피스의 지정된 영역인 경우, 서피스  에서 서피스
에서 서피스 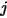 까지의 보기 계수는 서피스
까지의 보기 계수는 서피스  및
및 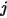 에서 방정식 2.301의 면적 평균입니다.
에서 방정식 2.301의 면적 평균입니다.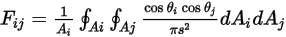
방정식 2.302
서피스-서피스 방사는 두 서피스가 서로 가시적이거나 보기 계수가 0이 아닌 경우에만 발생합니다. 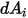 와
와 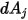 사이의 가시성과 관련된 기호
사이의 가시성과 관련된 기호 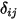 를 도입합니다.
를 도입합니다.
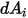 와
와 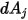 사이의 가시성과 관련된 기호
사이의 가시성과 관련된 기호 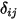 를 도입합니다.
를 도입합니다.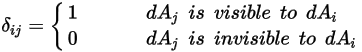
방정식 2.303
방정식 2.302를 다음과 같이 다시 작성할 수 있습니다.
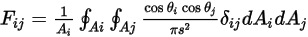
방정식 2.304
서로 가시적인 두 개의 서피스에 대해, 지정된 서피스  는 그림 2.378과 같이 서피스
는 그림 2.378과 같이 서피스 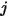 에서 나가는 방사 에너지의 일부만 방사합니다. 따라서 차원 보기 계수
에서 나가는 방사 에너지의 일부만 방사합니다. 따라서 차원 보기 계수 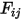 는 서피스
는 서피스  를 떠나서 서피스
를 떠나서 서피스 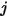 에 도달하는 에너지 부분을 나타냅니다. 다음과 같은 목록에 특성이 있습니다.
에 도달하는 에너지 부분을 나타냅니다. 다음과 같은 목록에 특성이 있습니다.
 는 그림 2.378과 같이 서피스
는 그림 2.378과 같이 서피스 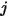 에서 나가는 방사 에너지의 일부만 방사합니다. 따라서 차원 보기 계수
에서 나가는 방사 에너지의 일부만 방사합니다. 따라서 차원 보기 계수 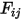 는 서피스
는 서피스  를 떠나서 서피스
를 떠나서 서피스 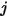 에 도달하는 에너지 부분을 나타냅니다. 다음과 같은 목록에 특성이 있습니다.
에 도달하는 에너지 부분을 나타냅니다. 다음과 같은 목록에 특성이 있습니다.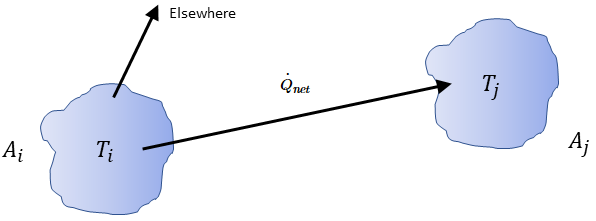
그림 2.378
• 보기 계수의 요약 - 서피스를 떠난 방사는 보존되기 때문에, 지정된 서피스  의 모든 보기 계수 합은 단일화됩니다.
의 모든 보기 계수 합은 단일화됩니다. 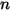 서피스 폐쇄형 시스템의 경우
서피스 폐쇄형 시스템의 경우
 의 모든 보기 계수 합은 단일화됩니다.
의 모든 보기 계수 합은 단일화됩니다. 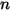 서피스 폐쇄형 시스템의 경우
서피스 폐쇄형 시스템의 경우
방정식 2.305
• 자체 보기 서피스 - 방사는 직선으로 진행하기 때문에 볼록한 서피스를 떠난 방사선이 나중에 동일한 서피스에 닿을 수 없습니다. 따라서 볼록 서피스는 자체 보기가 불가능합니다.
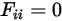
방정식 2.306
오목 서피스의 경우 서피스의 한 위치에서 나간 광선이 나중에 동일한 서피스의 다른 위치에 도달할 수 있습니다. 따라서 오목 서피스는 자체 보기가 가능합니다.
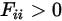
방정식 2.307
• 중첩 - 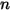 서피스 시스템의 경우, 주어진 서피스
서피스 시스템의 경우, 주어진 서피스  가
가 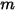 개의 서피스(
개의 서피스(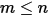 )에 방출되면 서피스
)에 방출되면 서피스  와
와  개의 서피스 사이의 보기 계수는 서피스
개의 서피스 사이의 보기 계수는 서피스  와
와 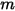 개의 서피스 사이의 보기 계수 합계와 같습니다.
개의 서피스 사이의 보기 계수 합계와 같습니다.
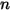 서피스 시스템의 경우, 주어진 서피스
서피스 시스템의 경우, 주어진 서피스  가
가 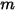 개의 서피스(
개의 서피스(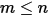 )에 방출되면 서피스
)에 방출되면 서피스  와
와  개의 서피스 사이의 보기 계수는 서피스
개의 서피스 사이의 보기 계수는 서피스  와
와 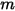 개의 서피스 사이의 보기 계수 합계와 같습니다.
개의 서피스 사이의 보기 계수 합계와 같습니다.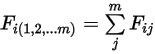
방정식 2.308
중첩 규칙 또는 합계 규칙은 지정된 차트나 그래프에서 형상을 사용할 수 없는 경우에 유용합니다. 중첩 규칙을 사용하면 알려진 형상의 합 또는 차이를 사용하여 구할 형상을 표현할 수 있습니다.
• 상반성 - 방정식 2.304는 보기 계수 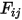 를 서피스
를 서피스  를 떠나는 방사 에너지와 서피스
를 떠나는 방사 에너지와 서피스 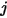 에 도달하는 방사 에너지의 분율로 정의합니다. 마찬가지로 서피스
에 도달하는 방사 에너지의 분율로 정의합니다. 마찬가지로 서피스 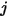 를 떠난 서피스
를 떠난 서피스  에 닿는 보기 계수
에 닿는 보기 계수 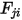 는 다음과 같이 표현됩니다.
는 다음과 같이 표현됩니다.
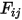 를 서피스
를 서피스  를 떠나는 방사 에너지와 서피스
를 떠나는 방사 에너지와 서피스 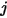 에 도달하는 방사 에너지의 분율로 정의합니다. 마찬가지로 서피스
에 도달하는 방사 에너지의 분율로 정의합니다. 마찬가지로 서피스 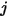 를 떠난 서피스
를 떠난 서피스  에 닿는 보기 계수
에 닿는 보기 계수 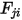 는 다음과 같이 표현됩니다.
는 다음과 같이 표현됩니다.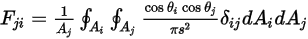
방정식 2.309
방정식 2.309를 방정식 2.304과 비교하면 다음과 같은 관계를 얻을 수 있습니다.
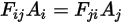
방정식 2.310
방정식 2.310을 보기 계수의 상반성이라고 합니다. 상반 정리를 사용하면 보기 계수 쌍 중 하나만 직접 계산할 수 있습니다.
클러스터링
S2S 방사 모델은 방사 서피스 수가 많은 경우 계산 비용이 높습니다. 필요한 계산 시간과 저장 공간을 줄이기 위해 인근 경계 셀 면을 일정 개수씩 그룹화해 서피스 클러스터를 생성하여 방사 서피스 수를 줄일 수 있습니다. 그러면 서피스 클러스터에 대한 라디오시티(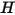 )가 계산됩니다. 이러한 값은 각 클러스터 내의 경계 셀 면에 분포되어 벽 온도가 계산됩니다. 방사 소스 항이 매우 비선형(온도의 4제곱에 비례)이기 때문에 서피스 클러스터의 평균 온도를 계산하고 클러스터를 형성하는 경계 면 사이에서 흐름 및 소스 항을 적절히 분배해야 합니다.
)가 계산됩니다. 이러한 값은 각 클러스터 내의 경계 셀 면에 분포되어 벽 온도가 계산됩니다. 방사 소스 항이 매우 비선형(온도의 4제곱에 비례)이기 때문에 서피스 클러스터의 평균 온도를 계산하고 클러스터를 형성하는 경계 면 사이에서 흐름 및 소스 항을 적절히 분배해야 합니다.
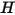 )가 계산됩니다. 이러한 값은 각 클러스터 내의 경계 셀 면에 분포되어 벽 온도가 계산됩니다. 방사 소스 항이 매우 비선형(온도의 4제곱에 비례)이기 때문에 서피스 클러스터의 평균 온도를 계산하고 클러스터를 형성하는 경계 면 사이에서 흐름 및 소스 항을 적절히 분배해야 합니다.
)가 계산됩니다. 이러한 값은 각 클러스터 내의 경계 셀 면에 분포되어 벽 온도가 계산됩니다. 방사 소스 항이 매우 비선형(온도의 4제곱에 비례)이기 때문에 서피스 클러스터의 평균 온도를 계산하고 클러스터를 형성하는 경계 면 사이에서 흐름 및 소스 항을 적절히 분배해야 합니다.서피스 클러스터 온도는 다음 방정식과 같이 영역-경계 면 온도의 평균을 통해 구합니다.
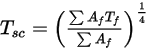
방정식 2.311
여기서 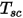 은 서피스 클러스터의 온도이고
은 서피스 클러스터의 온도이고 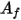 및
및 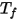 은 CFA 시뮬레이션에서 경계 셀의 면 영역과 온도입니다. 합은 서피스 클러스터 내의 모든 면에 대해 수행됩니다.
은 CFA 시뮬레이션에서 경계 셀의 면 영역과 온도입니다. 합은 서피스 클러스터 내의 모든 면에 대해 수행됩니다.
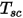 은 서피스 클러스터의 온도이고
은 서피스 클러스터의 온도이고 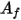 및
및 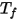 은 CFA 시뮬레이션에서 경계 셀의 면 영역과 온도입니다. 합은 서피스 클러스터 내의 모든 면에 대해 수행됩니다.
은 CFA 시뮬레이션에서 경계 셀의 면 영역과 온도입니다. 합은 서피스 클러스터 내의 모든 면에 대해 수행됩니다. ) 및 광선에 대한 방출 특성에 따라 방사 에너지를 회색 바디로 광선까지 배출합니다. 슈테판-볼츠만 법칙과, 배출과 흡수 간 상호 의존
) 및 광선에 대한 방출 특성에 따라 방사 에너지를 회색 바디로 광선까지 배출합니다. 슈테판-볼츠만 법칙과, 배출과 흡수 간 상호 의존