Fisica delle pareti
Legge logaritmica di parete
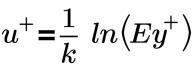
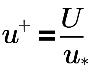
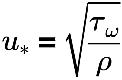
dove
u+ | Velocità adimensionale |
U | Velocità locale (centro cella) |
u* | Velocità di attrito |
τω | Taglio a parete |
ρ | Velocità del fluido |
E | Coefficiente costante |
k | Costante di Von Karman (0.41) |
y+ | distanza da parete a cella adimensionale |
Leggi e funzioni di parete
Una funzione di parete è necessaria per modellare il comportamento in prossimità della parete degli strati limite turbolenti in assenza di distribuzioni a griglia estremamente dense in corrispondenza di un limite (parete) senza slittamento. Nella letteratura è possibile trovare una vasta gamma di funzioni di parete ed è consigliabile cercare quella appropriata per una determinata applicazione. L'utilizzo di una funzione di parete è trattato nella teoria dello strato limite di Schlichting (Boundary Layer Theory, 6° edizione, 1968 ISBN 07-055329-7).
La distanza adimensionale y+ dalla parete a un punto nel flusso adiacente è definita come riportato di seguito.
dove
Velocità di attrito | |
v | Viscosità cinematica |
• Strato interno viscoso 0 < y+< 5
• Strato buffer 5 < y+< 30
• Strato inerziale 30 < y+< 200
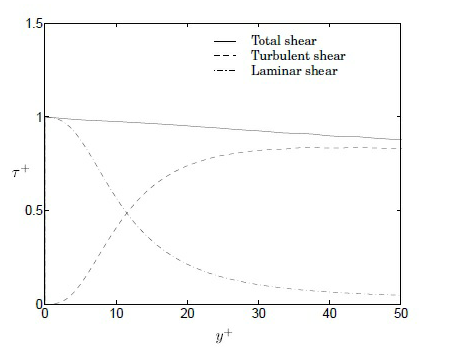
Per supportare i modelli di viscosità turbolenta qui illustrati sono state sviluppate diverse funzioni di parete.
• Standard - Proposta da Launder e Spalding, definisce il profilo di velocità turbolenta media in prossimità della parete. Con la funzione di parete Standard, la legge di parete per la distribuzione della velocità media viene formulata come descritto di seguito.
Nello strato interno inerziale e nello strato interno viscoso, si applica quanto segue.
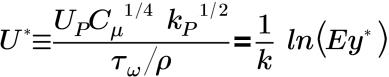
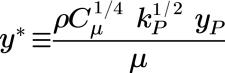
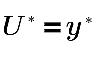
dove
k=0.4187 | Costante di Von Karman |
E=9.793 | Costante empirica |
UP | Velocità media del fluido nel punto P |
kP | Energia cinetica turbolenta nel punto P |
yP | Distanza dal punto P alla parete |
μ | Viscosità dinamica del fluido |
La funzione di parete Standard viene utilizzata in applicazioni industriali ed è inoltre descritta nei documenti sul flusso dei fluidi. È basata sul presupposto di un equilibrio locale tra la produzione di energia cinetica turbolenta K e il tasso di dissipazione dell'energia turbolenta. La funzione di parete Standard offre la massima precisione nella previsione di flussi con gradienti di pressione ridotti, nessuna separazione, nessun ricircolo ed effetti di accelerazione o decelerazione irrilevanti.
• Nonequilibrium(Kim) - Proposta da Kim, definisce il profilo di velocità turbolenta media in prossimità della parete. Con la funzione di parete Nonequilibrium(Kim), la legge di parete per la distribuzione della velocità media viene formulata come descritto di seguito.
Nello strato interno inerziale, si applica quanto segue.
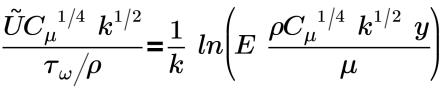
k=0.4187 | Costante di Von Karman |
E=9.793 | Costante empirica |
UP | Velocità media del fluido nel punto P |
kP | Velocità media dell'energia cinetica turbolenta del fluido nel punto P |
yP | Distanza dal punto P alla velocità media dell'energia cinetica turbolenta del fluido della parete nel punto P |
μ | Viscosità dinamica del fluido (velocità media dell'energia cinetica turbolenta del fluido) nel punto P |
Cμ | 0.09 |
La funzione di parete Nonequilibrium(Kim) presuppone che la produzione di energia cinetica turbolenta non sia uguale al tasso di dissipazione. La funzione di parete Nonequilibrium(Kim) considera gli effetti del gradiente di pressione. Utilizza un modello a due strati per il trattamento dello strato interno viscoso e dello strato inerziale completamente turbolento. La funzione di parete Nonequilibrium(Kim) adotta un trattamento della parete avanzato che utilizza funzioni di blend nella zona di buffer della parete (3 < y+ < 10) per una transizione uniforme tra la legge lineare nello strato interno viscoso e la legge logaritmica nello strato interno inerziale.
• Unified(Shih) - Proposta da Shih, definisce il profilo di velocità turbolenta media nello strato limite. Con la funzione di parete Unified(Shih), la legge di parete per la distribuzione della velocità media viene formulata come descritto di seguito.
Nell'intero strato limite, in cui sono presenti le funzioni di raccordo frammentarie f1(Yτ+) e f2(Yρ+), si applica quanto segue.
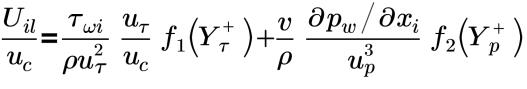
La funzione di parete Unified(Shih) è valida nello strato interno viscoso, nello strato buffer e nello strato interno inerziale (unificato). È appropriata per flussi con gradienti di pressione sia favorevoli sia sfavorevoli e flussi complessi delimitati da pareti con accelerazione, decelerazione e ricircolo. Questa funzione di parete utilizza un modello a tre strati per il trattamento dello strato interno viscoso, dello strato buffer e dello strato interno inerziale.
Modello di rugosità della parete
Modello rugosità parete (Wall Roughness Model) fa riferimento alla rugosità in termini di finitura di superficie su una parete.
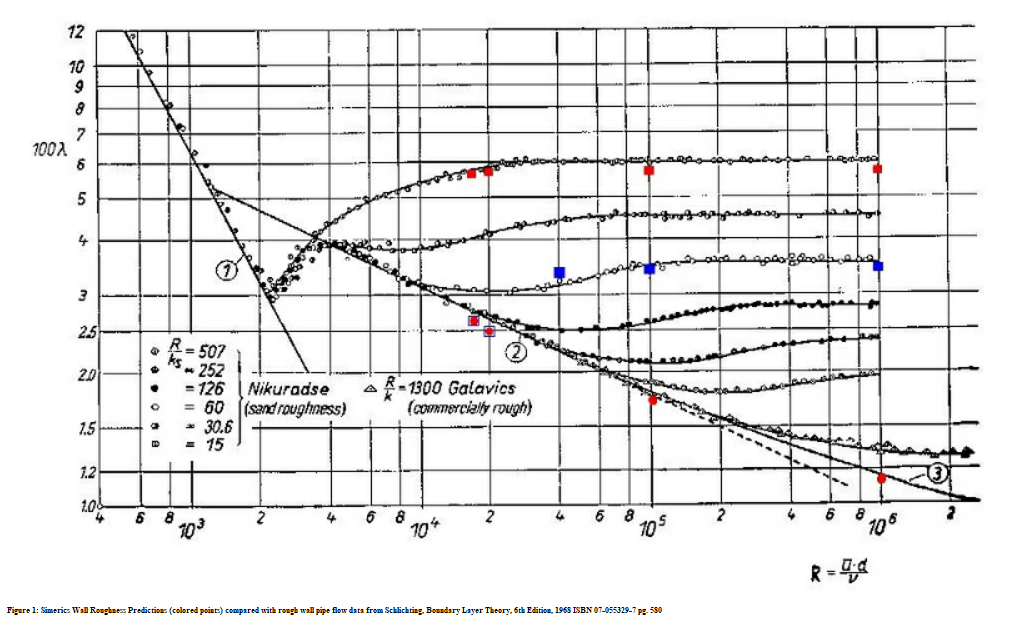
Previsioni della rugosità della parete di Creo Flow Analysis (punti colorati) rispetto ai dati di flusso di tubi con parete rugosa tratti da Schlichting, Boundary Layer Theory, 6° edizione, 1968 ISBN 07-055329-7, pagina 580.