Fisica
Per un flusso multicomponente, si risolvono le equazioni di trasporto scalari per la velocità, la pressione, la temperatura, la turbolenza e altre grandezze fisiche della miscela. Quando sono presenti più componenti, è necessario risolvere equazioni aggiuntive per determinare come vengono trasportati i componenti all'interno della miscela fluida.
Descrizione delle diverse specie (componenti)
Per quantificare il contenuto di un componente  in un flusso di
in un flusso di 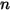 componenti esistono più variabili diverse ma correlate:
componenti esistono più variabili diverse ma correlate:
 in un flusso di
in un flusso di 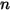 componenti esistono più variabili diverse ma correlate:
componenti esistono più variabili diverse ma correlate: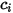 | concentrazione molare del componente  |
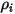 | concentrazione di massa del componente  |
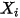 | frazione molare del componente  |
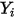 | frazione di massa del componente  |
Le quattro grandezze sono correlate come segue:
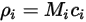
Equazione 2.314
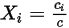
Equazione 2.315
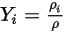
Equazione 2.316
dove
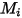 | peso molecolare del componente  |
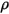 | densità della miscela |
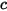 | somma delle concentrazioni molari di tutti i componenti in un sistema |
e
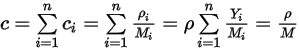
Equazione 2.317
dove 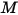 è il peso molecolare della miscela:
è il peso molecolare della miscela:
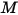 è il peso molecolare della miscela:
è il peso molecolare della miscela: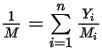
Equazione 2.318
L'equazione 2.317 indica che, con il peso molecolare ponderato della frazione di massa per la miscela, l'equazione 2.314 si applica anche alla miscela di 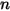 componenti.
componenti.
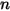 componenti.
componenti.Dalle definizioni dell'equazione 2.315 e dell'equazione 2.316, inoltre, la somma della frazione molare e della frazione di massa deve essere l'unità:
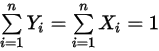
Equazione 2.319
Nei solutori CFA è possibile ottenere direttamente la frazione di massa del componente arbitrario 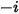 ,
, 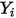 risolvendo le equazioni di trasporto differenziali parziali. Le altre variabili,
risolvendo le equazioni di trasporto differenziali parziali. Le altre variabili, 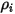 ,
, 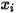 e
e 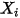 , sono variabili ausiliarie utilizzate per la postelaborazione.
, sono variabili ausiliarie utilizzate per la postelaborazione.
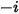 ,
, 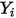 risolvendo le equazioni di trasporto differenziali parziali. Le altre variabili,
risolvendo le equazioni di trasporto differenziali parziali. Le altre variabili, 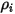 ,
, 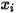 e
e 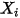 , sono variabili ausiliarie utilizzate per la postelaborazione.
, sono variabili ausiliarie utilizzate per la postelaborazione.Equazioni governanti
In un flusso multicomponente, il movimento di massa della miscela viene modellato mediante i singoli campi di velocità, pressione, temperatura e turbolenza. Per la miscelazione e il trasporto delle specie chimiche, ogni componente dispone di una specifica equazione governante per la conservazione della massa. L'influenza di più componenti sul flusso di massa viene rilevata tramite la variazione delle proprietà della miscela, come la densità e la viscosità, con le proprietà e le frazioni di massa locali dei componenti.
• Equazioni della frazione di massa
Per il flusso della miscela di 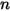 componenti, se non sono presenti reazioni chimiche, il trasporto di un componente arbitrario
componenti, se non sono presenti reazioni chimiche, il trasporto di un componente arbitrario  è regolato dall'equazione seguente:
è regolato dall'equazione seguente:
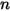 componenti, se non sono presenti reazioni chimiche, il trasporto di un componente arbitrario
componenti, se non sono presenti reazioni chimiche, il trasporto di un componente arbitrario  è regolato dall'equazione seguente:
è regolato dall'equazione seguente: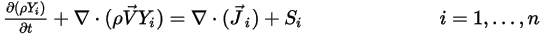
Equazione 2.320
dove
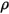 e e 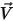 | densità e velocità della miscela |
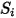 | qualsiasi fonte definita dall'utente |
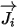 | termine di diffusione della massa |
Per i flussi laminari, il vettore di velocità 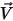 e la frazione di massa
e la frazione di massa 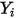 sono variabili istantanee. Per i flussi turbolenti, questi vettori di velocità sono grandezze mediate secondo Favre, poiché i flussi multicomponente vengono considerati come flussi comprimibili o a densità variabile.
sono variabili istantanee. Per i flussi turbolenti, questi vettori di velocità sono grandezze mediate secondo Favre, poiché i flussi multicomponente vengono considerati come flussi comprimibili o a densità variabile.
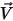 e la frazione di massa
e la frazione di massa 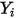 sono variabili istantanee. Per i flussi turbolenti, questi vettori di velocità sono grandezze mediate secondo Favre, poiché i flussi multicomponente vengono considerati come flussi comprimibili o a densità variabile.
sono variabili istantanee. Per i flussi turbolenti, questi vettori di velocità sono grandezze mediate secondo Favre, poiché i flussi multicomponente vengono considerati come flussi comprimibili o a densità variabile.Nell'equazione 2.320, le grandezze della miscela e il termine di diffusione della massa sono definiti come descritto di seguito.
◦ Densità della miscela - Valore mediato sulla massa delle densità di tutti i componenti:
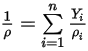
Equazione 2.321
Per una miscela di specie gassose, la densità della miscela viene calcolata mediante la legge dei gas perfetti in base al peso molecolare della miscela 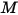 , calcolato con l'equazione 2.318:
, calcolato con l'equazione 2.318:
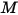 , calcolato con l'equazione 2.318:
, calcolato con l'equazione 2.318: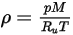
Equazione 2.322
dove
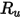 | costante universale del gas |
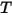 | temperatura della miscela |
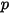 | pressione assoluta |
Se utilizzate la pressione di esercizio (costante), l'equazione 2.322 si riduce alla cosiddetta legge dei gas perfetti incomprimibili. Questo presupposto è appropriato per la miscelazione e il trasporto delle specie, perché la pressione manometrica è in genere trascurabile rispetto alla pressione di esercizio.
◦ Velocità della miscela - Valore mediato sulla massa delle velocità di tutti i componenti:
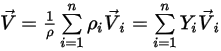
Equazione 2.323
Poiché viene risolta una sola velocità, tuttavia, presupponete che la velocità della miscela e le velocità di tutti i componenti abbiano gli stessi valori.
◦ Flusso di diffusione della massa - Il flusso di diffusione della massa del componente  è costituito da due parti, il termine di diffusione laminare e quello di diffusione turbolenta, espresse come segue:
è costituito da due parti, il termine di diffusione laminare e quello di diffusione turbolenta, espresse come segue:
 è costituito da due parti, il termine di diffusione laminare e quello di diffusione turbolenta, espresse come segue:
è costituito da due parti, il termine di diffusione laminare e quello di diffusione turbolenta, espresse come segue: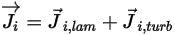
Equazione 2.324
Nell'equazione 2.324, 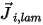 è il flusso di diffusione laminare del componente
è il flusso di diffusione laminare del componente  causato dai gradienti di concentrazione e di temperatura. Per default, Creo Flow Analysis utilizza l'approssimazione della diluizione o la legge di Fick per modellare la diffusione della massa causata dai gradienti di concentrazione. La formula del flusso di diffusione laminare è la seguente:
causato dai gradienti di concentrazione e di temperatura. Per default, Creo Flow Analysis utilizza l'approssimazione della diluizione o la legge di Fick per modellare la diffusione della massa causata dai gradienti di concentrazione. La formula del flusso di diffusione laminare è la seguente:
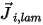 è il flusso di diffusione laminare del componente
è il flusso di diffusione laminare del componente  causato dai gradienti di concentrazione e di temperatura. Per default, Creo Flow Analysis utilizza l'approssimazione della diluizione o la legge di Fick per modellare la diffusione della massa causata dai gradienti di concentrazione. La formula del flusso di diffusione laminare è la seguente:
causato dai gradienti di concentrazione e di temperatura. Per default, Creo Flow Analysis utilizza l'approssimazione della diluizione o la legge di Fick per modellare la diffusione della massa causata dai gradienti di concentrazione. La formula del flusso di diffusione laminare è la seguente: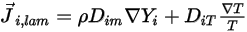
Equazione 2.325
dove 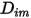 è il coefficiente di diffusione della massa per il componente
è il coefficiente di diffusione della massa per il componente  nella miscela e
nella miscela e 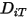 è il coefficiente di diffusione termica (Soret).
è il coefficiente di diffusione termica (Soret).
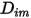 è il coefficiente di diffusione della massa per il componente
è il coefficiente di diffusione della massa per il componente  nella miscela e
nella miscela e 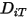 è il coefficiente di diffusione termica (Soret).
è il coefficiente di diffusione termica (Soret).Per i flussi turbolenti, il termine fluttuante derivato dal calcolo di Favre della media dell'avvezione nell'equazione 2.320 viene modellato come diffusione turbolenta:
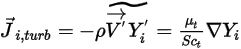
Equazione 2.326
dove
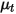 | viscosità turbolenta |
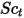 | numero di turbolenza di Schmidt 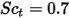 per default per default |
La diffusione turbolenta generalmente travolge la diffusione laminare. La specifica delle proprietà di diffusione laminare dettagliate nei flussi turbolenti è in genere meno importante della controparte turbolenta.
Per derivare l'equazione di continuità della massa per il flusso della miscela, aggiungete tutte le equazioni della frazione di massa dei componenti e applicate l'equazione 2.319:
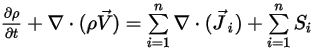
Equazione 2.327
Per la conservazione della massa totale del flusso della miscela, la somma dei termini di diffusione di tutti i componenti deve essere uguale a zero.
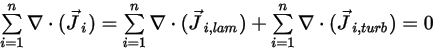
Equazione 2.328
Dall'equazione 2.319 e dall'equazione 2.326, il termine di diffusione turbolenta è sempre determinato come uguale a zero. Di conseguenza, per i flussi completamente turbolenti, l'equazione 2.328 viene in genere considerata automaticamente soddisfatta. Per i flussi laminari, o quando non è possibile ignorare la diffusione di massa laminare nei flussi turbolenti, l'equazione 2.328 si riduce invece alla forma seguente:
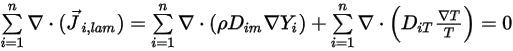
Equazione 2.329
Per soddisfare l'equazione 2.329, applicate quindi i due vincoli distinti:
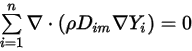
Equazione 2.330
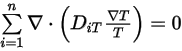
Equazione 2.331
La forma finale dell'equazione di continuità dei flussi multicomponente è la seguente:
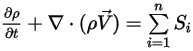
Equazione 2.332
• Coefficienti di diffusione
Per risolvere l'equazione 2.320 di trasporto per i flussi laminari multicomponente, è necessario il coefficiente di diffusione di massa 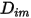 e il coefficiente di diffusione termica
e il coefficiente di diffusione termica 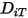 per ciascun componente di una miscela. Di seguito sono illustrati i metodi per determinare
per ciascun componente di una miscela. Di seguito sono illustrati i metodi per determinare 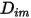 e
e 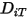 .
.
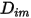 e il coefficiente di diffusione termica
e il coefficiente di diffusione termica 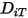 per ciascun componente di una miscela. Di seguito sono illustrati i metodi per determinare
per ciascun componente di una miscela. Di seguito sono illustrati i metodi per determinare 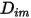 e
e 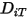 .
.◦ Coefficienti di diffusione di massa - La formula del flusso di diffusione di massa nei flussi laminari (equazione 2.325) è valida quando la composizione della miscela non cambia o quando 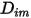 è indipendente dalla composizione. Questa approssimazione è accettabile per le miscele diluite quando il valore di
è indipendente dalla composizione. Questa approssimazione è accettabile per le miscele diluite quando il valore di 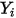 è molto ridotto per tutti i componenti tranne per il gas portante. Per le miscele non diluite in flussi laminari multicomponente, calcolate
è molto ridotto per tutti i componenti tranne per il gas portante. Per le miscele non diluite in flussi laminari multicomponente, calcolate 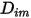 dalla formula seguente:
dalla formula seguente:
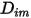 è indipendente dalla composizione. Questa approssimazione è accettabile per le miscele diluite quando il valore di
è indipendente dalla composizione. Questa approssimazione è accettabile per le miscele diluite quando il valore di 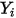 è molto ridotto per tutti i componenti tranne per il gas portante. Per le miscele non diluite in flussi laminari multicomponente, calcolate
è molto ridotto per tutti i componenti tranne per il gas portante. Per le miscele non diluite in flussi laminari multicomponente, calcolate 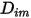 dalla formula seguente:
dalla formula seguente: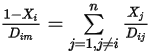
Equazione 2.333
dove 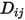 è il coefficiente di diffusione di massa binario del componente
è il coefficiente di diffusione di massa binario del componente  nel componente
nel componente 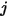 da specificare o calcolare.
da specificare o calcolare.
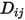 è il coefficiente di diffusione di massa binario del componente
è il coefficiente di diffusione di massa binario del componente  nel componente
nel componente 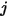 da specificare o calcolare.
da specificare o calcolare.◦ Valore specificato - Il coefficiente di diffusione di massa binario 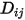 è una costante o una funzione di temperatura, se viene tenuto conto del trasferimento di calore. È possibile specificare il valore direttamente oppure ottenerlo dal numero di Schmidt specificato:
è una costante o una funzione di temperatura, se viene tenuto conto del trasferimento di calore. È possibile specificare il valore direttamente oppure ottenerlo dal numero di Schmidt specificato:
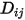 è una costante o una funzione di temperatura, se viene tenuto conto del trasferimento di calore. È possibile specificare il valore direttamente oppure ottenerlo dal numero di Schmidt specificato:
è una costante o una funzione di temperatura, se viene tenuto conto del trasferimento di calore. È possibile specificare il valore direttamente oppure ottenerlo dal numero di Schmidt specificato: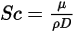
Equazione 2.334
dove
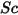 | Numero di Schmidt |
Il numero di Schmidt è definito come rapporto tra tasso di diffusione viscosa e tasso di diffusione molecolare (massa).
Se per tutti i componenti viene applicato un valore o una funzione di temperatura, l'equazione 2.333 si riduce a:
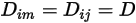
Equazione 2.335
L'equazione 2.335 è un'approssimazione appropriata per la modellazione di una miscela diluita, con specie presenti in frazioni di massa basse in un fluido portante con concentrazione elevata. In questi casi, definite 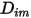 direttamente come costante o funzione di temperatura.
direttamente come costante o funzione di temperatura.
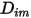 direttamente come costante o funzione di temperatura.
direttamente come costante o funzione di temperatura.Per le miscele non diluite, invece, con il coefficiente 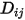 specificato utilizzate l'equazione 2.333 per calcolare il singolo coefficiente di diffusione di massa nella miscela,
specificato utilizzate l'equazione 2.333 per calcolare il singolo coefficiente di diffusione di massa nella miscela, 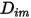 .
.
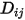 specificato utilizzate l'equazione 2.333 per calcolare il singolo coefficiente di diffusione di massa nella miscela,
specificato utilizzate l'equazione 2.333 per calcolare il singolo coefficiente di diffusione di massa nella miscela, 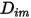 .
.◦ Teoria cinetica - Per un gas perfetto, il coefficiente di diffusione di massa binario 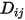 può essere ottenuto anche mediante la teoria cinetica.
può essere ottenuto anche mediante la teoria cinetica.
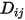 può essere ottenuto anche mediante la teoria cinetica.
può essere ottenuto anche mediante la teoria cinetica.Fonte: H. A. McGee, "Molecular Engineering", McGraw-Hill, New York, 1991
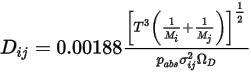
Equazione 2.336
dove 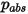 è la pressione assoluta e
è la pressione assoluta e 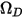 è l'integrale di collisione della diffusione, che è una misura dell'interazione delle molecole nel sistema.
è l'integrale di collisione della diffusione, che è una misura dell'interazione delle molecole nel sistema. 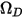 è una funzione della grandezza
è una funzione della grandezza 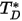 , definita come segue:
, definita come segue:
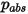 è la pressione assoluta e
è la pressione assoluta e 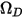 è l'integrale di collisione della diffusione, che è una misura dell'interazione delle molecole nel sistema.
è l'integrale di collisione della diffusione, che è una misura dell'interazione delle molecole nel sistema. 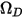 è una funzione della grandezza
è una funzione della grandezza 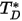 , definita come segue:
, definita come segue: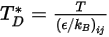
Equazione 2.337
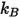 è la costante di Boltzmann, definita dalla divisione della costante universale dei gas
è la costante di Boltzmann, definita dalla divisione della costante universale dei gas 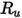 per il numero di Avogadro. Per la miscela,
per il numero di Avogadro. Per la miscela, 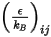 è la media geometrica:
è la media geometrica: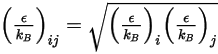
Equazione 2.338
Per una miscela binaria, 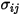 viene calcolato come media aritmetica dei singoli valori di
viene calcolato come media aritmetica dei singoli valori di 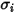 e
e 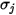 :
:
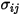 viene calcolato come media aritmetica dei singoli valori di
viene calcolato come media aritmetica dei singoli valori di 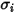 e
e 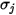 :
: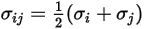
Equazione 2.339
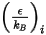 e
e 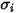 sono i parametri di Lennard-Jones per il componente
sono i parametri di Lennard-Jones per il componente  della miscela. Nello specifico,
della miscela. Nello specifico, 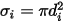 è la sezione trasversale di collisione della molecola della sfera con diametro
è la sezione trasversale di collisione della molecola della sfera con diametro 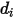 (una molecola si estende su un'area pari al doppio del suo diametro, poiché anche le molecole con cui entra in collisione hanno diametro
(una molecola si estende su un'area pari al doppio del suo diametro, poiché anche le molecole con cui entra in collisione hanno diametro 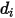 ), mentre
), mentre 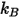 =1.38064852(79) ×10-23(J/K) è la costante di Boltzmann.
=1.38064852(79) ×10-23(J/K) è la costante di Boltzmann.In Creo Flow Analysis, si specificano il diametro 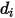 e l'energia
e l'energia 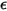 per determinare i due parametri di Lennard-Jones.
per determinare i due parametri di Lennard-Jones.
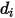 e l'energia
e l'energia 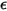 per determinare i due parametri di Lennard-Jones.
per determinare i due parametri di Lennard-Jones.◦ Coefficienti di diffusione termica 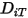 - I coefficienti di diffusione termica possono essere definiti come costanti, funzioni polinomiali di temperatura, funzioni definite dall'utente o utilizzando l'espressione dipendente dalla composizione empirica seguente derivata da:
- I coefficienti di diffusione termica possono essere definiti come costanti, funzioni polinomiali di temperatura, funzioni definite dall'utente o utilizzando l'espressione dipendente dalla composizione empirica seguente derivata da:
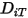 - I coefficienti di diffusione termica possono essere definiti come costanti, funzioni polinomiali di temperatura, funzioni definite dall'utente o utilizzando l'espressione dipendente dalla composizione empirica seguente derivata da:
- I coefficienti di diffusione termica possono essere definiti come costanti, funzioni polinomiali di temperatura, funzioni definite dall'utente o utilizzando l'espressione dipendente dalla composizione empirica seguente derivata da:Riferimenti: K. K. Y. Kuo, "Principles of Combustion", John Wiley and Sons, New York, 1986.
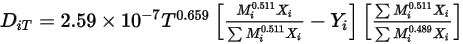
Equazione 2.340
Questa forma del coefficiente di diffusione termica causa una diffusione meno rapida delle molecole pesanti e una diffusione più rapida delle molecole leggere verso le superfici riscaldate.
• Equazioni del momento
Con le velocità e le proprietà ponderate sulla massa, le equazioni del momento per la miscela di tutti i componenti presentano la stessa espressione di quelle per i flussi dei singoli fluidi:
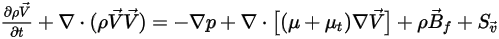
Equazione 2.341
dove la densità e la velocità della miscela vengono calcolate mediante l'equazione 2.321, l'equazione 2.322 e l'equazione 2.323. La viscosità turbolenta viene calcolata direttamente dai modelli di turbolenza in base al flusso della miscela, in modo che il valore sia indipendente dai componenti. La viscosità laminare viene calcolata come descritto di seguito.
◦ Viscosità laminare mediata sulla massa - Per le miscele di gas non perfetti, la viscosità della miscela viene calcolata in base a una media della frazione di massa delle viscosità delle specie chimiche pure (componenti):
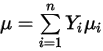
Equazione 2.342
◦ Teoria cinetica - Per le miscele di gas perfetti, la viscosità della miscela viene calcolata in base alla teoria cinetica. Per ogni componente, la viscosità dinamica è basata sull'equazione di Boltzmann:
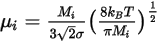
Equazione 2.343
Per la diffusività di massa, sono necessari i parametri di Lennard-Jones, 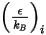 e
e 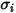 , per calcolare la viscosità dei gas componenti una miscela.
, per calcolare la viscosità dei gas componenti una miscela.
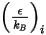 e
e 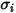 , per calcolare la viscosità dei gas componenti una miscela.
, per calcolare la viscosità dei gas componenti una miscela.Per la miscela di gas perfetti, la viscosità viene quindi calcolata come segue:
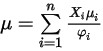
Equazione 2.344
dove
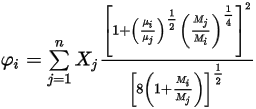
Equazione 2.345
• Equazione di energia
Come descritto per il modulo Calore (Heat), l'equazione di energia per la miscela di tutti i componenti è espressa come segue:
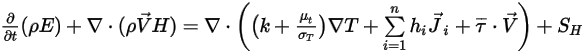
Equazione 2.346
dove 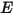 e
e 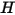 sono l'energia interna totale e l'entalpia totale della miscela di
sono l'energia interna totale e l'entalpia totale della miscela di 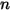 componenti. Insieme al calore specifico della miscela
componenti. Insieme al calore specifico della miscela 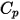 e all'entalpia statica
e all'entalpia statica 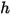 , vengono ottenute calcolando la media di massa dei valori corrispondenti di ciascun componente:
, vengono ottenute calcolando la media di massa dei valori corrispondenti di ciascun componente:
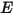 e
e 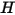 sono l'energia interna totale e l'entalpia totale della miscela di
sono l'energia interna totale e l'entalpia totale della miscela di 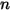 componenti. Insieme al calore specifico della miscela
componenti. Insieme al calore specifico della miscela 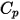 e all'entalpia statica
e all'entalpia statica 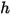 , vengono ottenute calcolando la media di massa dei valori corrispondenti di ciascun componente:
, vengono ottenute calcolando la media di massa dei valori corrispondenti di ciascun componente:◦ Capacità termica della miscela mediata sulla massa
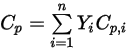
Equazione 2.347
◦ Energia ed entalpia della miscela mediate sulla massa
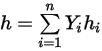
Equazione 2.348
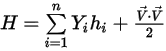
Equazione 2.349
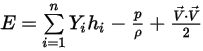
Equazione 2.350
L'entalpia statica di un componente è costituita da due parti: l'entalpia di riferimento dello stato standard e l'entalpia sensibile. Per i flussi multicomponente, includete entrambe le parti dell'entalpia (valore assoluto o totale) durante il calcolo di 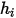 .
.
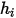 .
.Nell'equazione 2.336, il primo termine sul lato destro rappresenta la diffusione dell'energia. È costituito da tre parti: la conduzione termica, il trasporto di energia causato dalla diffusione della specie e il riscaldamento viscoso. Per la conduzione termica della miscela, la modellazione viene eseguita così come per il flusso di un singolo fluido. In Creo Flow Analysis, la conduttività termica della miscela viene calcolata nel modo seguente:
◦ Conduttività termica mediata sulla massa - Per le miscele di gas non perfetti, la conduttività termica della miscela viene calcolata in base a una semplice media della frazione di massa delle conduttività termiche delle specie pure (componenti):
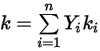
Equazione 2.351
Questo è il metodo di default in Creo Flow Analysis.
◦ Teoria cinetica - Per le miscele di gas perfetti, la conduttività termica della miscela può essere calcolata in base alla teoria cinetica. Per ogni componente, la conduttività termica ha la forma seguente:
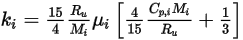
Equazione 2.352
dove
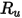 | costante universale del gas |
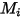 | peso molecolare |
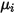 | viscosità calcolata o specificata del componente |
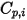 | capacità termica specifica calcolata o specificata del componente |
Tenete presente che, così come la viscosità laminare 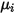 , anche il calore specifico
, anche il calore specifico 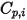 può essere ottenuto mediante la teoria cinetica:
può essere ottenuto mediante la teoria cinetica:
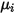 , anche il calore specifico
, anche il calore specifico 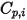 può essere ottenuto mediante la teoria cinetica:
può essere ottenuto mediante la teoria cinetica: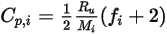
Equazione 2.353
dove 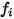 è il numero di modalità di immagazzinamento dell'energia (gradi di libertà) per il gas componente
è il numero di modalità di immagazzinamento dell'energia (gradi di libertà) per il gas componente  .
.
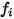 è il numero di modalità di immagazzinamento dell'energia (gradi di libertà) per il gas componente
è il numero di modalità di immagazzinamento dell'energia (gradi di libertà) per il gas componente  .
.La conduttività termica per la miscela di gas perfetti viene quindi calcolata come segue:
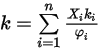
Equazione 2.354
dove 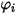 è espresso nell'equazione 2.335.
è espresso nell'equazione 2.335.
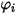 è espresso nell'equazione 2.335.
è espresso nell'equazione 2.335.Il secondo termine di diffusione
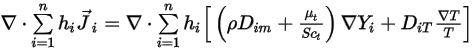
Equazione 2.355
rappresenta il trasporto dell'entalpia causato dalla diffusione della specie chimica nel flusso di 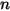 componenti. Questo termine può avere un effetto significativo sul campo di entalpia e non deve essere trascurato. Quando il numero di Lewis, il rapporto tra diffusività termica
componenti. Questo termine può avere un effetto significativo sul campo di entalpia e non deve essere trascurato. Quando il numero di Lewis, il rapporto tra diffusività termica 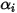 e diffusività di massa
e diffusività di massa 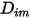 :
:
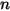 componenti. Questo termine può avere un effetto significativo sul campo di entalpia e non deve essere trascurato. Quando il numero di Lewis, il rapporto tra diffusività termica
componenti. Questo termine può avere un effetto significativo sul campo di entalpia e non deve essere trascurato. Quando il numero di Lewis, il rapporto tra diffusività termica 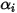 e diffusività di massa
e diffusività di massa 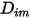 :
: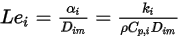
Equazione 2.356
poiché qualsiasi specie non è unità, trascurare questo termine può determinare errori importanti.
Il terzo termine di diffusione è il contributo di riscaldamento viscoso 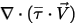 . Nonostante venga trattato come nel flusso di un singolo fluido, calcolate la tensione tangenziale
. Nonostante venga trattato come nel flusso di un singolo fluido, calcolate la tensione tangenziale 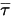 utilizzando la viscosità laminare e quella turbolenta della miscela. Il termine della fonte generale
utilizzando la viscosità laminare e quella turbolenta della miscela. Il termine della fonte generale 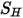 è la fonte di calore totale esterna o definita dall'utente per tutti i componenti.
è la fonte di calore totale esterna o definita dall'utente per tutti i componenti.
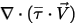 . Nonostante venga trattato come nel flusso di un singolo fluido, calcolate la tensione tangenziale
. Nonostante venga trattato come nel flusso di un singolo fluido, calcolate la tensione tangenziale 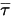 utilizzando la viscosità laminare e quella turbolenta della miscela. Il termine della fonte generale
utilizzando la viscosità laminare e quella turbolenta della miscela. Il termine della fonte generale 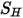 è la fonte di calore totale esterna o definita dall'utente per tutti i componenti.
è la fonte di calore totale esterna o definita dall'utente per tutti i componenti.• Modelli di turbolenza - Con la densità 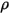 , la viscosità molecolare
, la viscosità molecolare 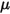 e la velocità
e la velocità 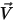 della miscela, le equazioni di modellazione della turbolenza nei modelli k-ε standard e k-ε RNG presentano le stesse forme generali riscontrate nei modelli di turbolenza dei singoli fluidi, descritte per il modulo Turbolenza (Turbulence). La viscosità turbolenta per la miscela
della miscela, le equazioni di modellazione della turbolenza nei modelli k-ε standard e k-ε RNG presentano le stesse forme generali riscontrate nei modelli di turbolenza dei singoli fluidi, descritte per il modulo Turbolenza (Turbulence). La viscosità turbolenta per la miscela 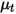 viene calcolata direttamente dall'espressione seguente:
viene calcolata direttamente dall'espressione seguente:
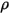 , la viscosità molecolare
, la viscosità molecolare 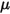 e la velocità
e la velocità 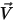 della miscela, le equazioni di modellazione della turbolenza nei modelli k-ε standard e k-ε RNG presentano le stesse forme generali riscontrate nei modelli di turbolenza dei singoli fluidi, descritte per il modulo Turbolenza (Turbulence). La viscosità turbolenta per la miscela
della miscela, le equazioni di modellazione della turbolenza nei modelli k-ε standard e k-ε RNG presentano le stesse forme generali riscontrate nei modelli di turbolenza dei singoli fluidi, descritte per il modulo Turbolenza (Turbulence). La viscosità turbolenta per la miscela 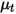 viene calcolata direttamente dall'espressione seguente:
viene calcolata direttamente dall'espressione seguente: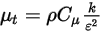
Equazione 2.357
La produzione di energia cinetica turbolenta, inoltre, viene calcolata in base ai gradienti di velocità e viscosità turbolenta della miscela.
Modellazione di limiti multicomponente
In un flusso multicomponente, le condizioni al limite per le equazioni di modellazione di flusso, energia e turbolenza sono uguali a quelle nei flussi monofase, descritte nei moduli Flusso (Flow), Calore (Heat) e Turbolenza (Turbulence). Per le frazioni di massa di un componente, le condizioni al limite sono costituite dal valore specificato, dalla portata volumetrica specificata e/o dal gradiente.
• Limite di entrata per n-componenti
A un limite di entrata, il trasporto netto di un componente può essere costituito da contributi sia di convezione sia di diffusione. La convezione è determinata dalla frazione di massa della specie in entrata specificata. La diffusione dipende dal gradiente del campo della frazione di massa calcolata. A una velocità di entrata convettiva molto ridotta, è possibile acquisire o perdere massa sostanziale attraverso l'entrata a causa della diffusione. Per questo motivo, la diffusione in entrata non è inclusa per default, ma può essere attivata come opzione.
◦ Valore specificato - Per il flusso di 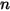 componenti, le frazioni di massa in entrata sono predeterminate per
componenti, le frazioni di massa in entrata sono predeterminate per 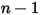 componenti, mentre la frazione di massa del
componenti, mentre la frazione di massa del 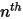 componente viene ottenuta mediante l'equazione 2.319 del vincolo fisico:
componente viene ottenuta mediante l'equazione 2.319 del vincolo fisico:
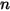 componenti, le frazioni di massa in entrata sono predeterminate per
componenti, le frazioni di massa in entrata sono predeterminate per 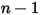 componenti, mentre la frazione di massa del
componenti, mentre la frazione di massa del 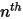 componente viene ottenuta mediante l'equazione 2.319 del vincolo fisico:
componente viene ottenuta mediante l'equazione 2.319 del vincolo fisico:
Equazione 2.358
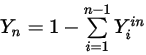
Equazione 2.359
La frazione di massa per ciascun componente, inoltre, deve essere non negativa.
◦ Portata volumetrica specificata - Supponendo che 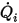 sia la portata volumetrica in entrata predescritta per il componente
sia la portata volumetrica in entrata predescritta per il componente  , la portata di ciascun componente
, la portata di ciascun componente 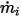 e la portata totale all'entrata
e la portata totale all'entrata 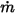 sono:
sono:
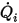 sia la portata volumetrica in entrata predescritta per il componente
sia la portata volumetrica in entrata predescritta per il componente  , la portata di ciascun componente
, la portata di ciascun componente 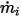 e la portata totale all'entrata
e la portata totale all'entrata 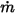 sono:
sono:
Equazione 2.360
dove 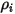 è la densità in entrata del componente
è la densità in entrata del componente  .
.
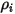 è la densità in entrata del componente
è la densità in entrata del componente  .
.Per definizione, la frazione di massa viene calcolata come segue:
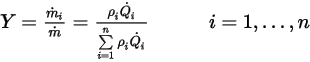
Equazione 2.361
◦ Limiti di uscita, simmetria e parete - Per 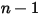 componenti, le condizioni a gradiente zero si applicano a tutti i limiti di uscita, simmetria e parete, mentre la
componenti, le condizioni a gradiente zero si applicano a tutti i limiti di uscita, simmetria e parete, mentre la 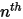 fase viene ottenuta mediante il vincolo fisico:
fase viene ottenuta mediante il vincolo fisico:
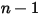 componenti, le condizioni a gradiente zero si applicano a tutti i limiti di uscita, simmetria e parete, mentre la
componenti, le condizioni a gradiente zero si applicano a tutti i limiti di uscita, simmetria e parete, mentre la 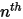 fase viene ottenuta mediante il vincolo fisico:
fase viene ottenuta mediante il vincolo fisico: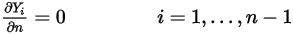
Equazione 2.362
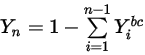
Equazione 2.363
dove 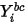 è il valore limite ottenuto dall'equazione 2.347.
è il valore limite ottenuto dall'equazione 2.347.
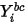 è il valore limite ottenuto dall'equazione 2.347.
è il valore limite ottenuto dall'equazione 2.347.Considerazioni numeriche
Le equazioni governanti, i modelli di turbolenza e le condizioni al limite riportati sopra costituiscono la base del modello di miscelazione di più componenti. Senza termini di fonte esterna o definita dall'utente e reazioni chimiche, sono un sistema chiuso di equazioni che è possibile risolvere numericamente utilizzando un solutore a volumi finiti basato sulla pressione.
Le equazioni di trasporto della frazione di massa vengono risolte per tutti i componenti. Per soddisfare il vincolo fisico, le frazioni di massa effettive vengono scalate della somma dei valori risolti per tutti i componenti:

Equazione 2.364
dove 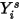 è il valore ottenuto dalla risoluzione dell'equazione 2.320. La frazione di massa effettiva è:
è il valore ottenuto dalla risoluzione dell'equazione 2.320. La frazione di massa effettiva è:
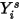 è il valore ottenuto dalla risoluzione dell'equazione 2.320. La frazione di massa effettiva è:
è il valore ottenuto dalla risoluzione dell'equazione 2.320. La frazione di massa effettiva è: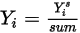
Equazione 2.365