Physik
Für einen Mehrkomponenten-Fluss lösen Sie die skalaren Transportgleichungen für die Mischungsgeschwindigkeit, den Druck, die Temperatur, die Turbulenzen und andere physikalische Größen. Wenn mehrere Komponenten vorhanden sind, müssen Sie zusätzliche Gleichungen lösen, um zu bestimmen, wie die Komponenten innerhalb des Flüssigkeitsgemischs transportiert werden.
Beschreibung der mehrfachen Spezies (Komponente)
Es gibt verschiedene, jedoch einander zugehörige Variablen, um den Inhalt einer Komponente  im Komponentenfluss
im Komponentenfluss  zu quantifizieren:
zu quantifizieren:
 im Komponentenfluss
im Komponentenfluss  zu quantifizieren:
zu quantifizieren: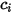 | molare Konzentration der Komponente  |
 | Massenkonzentration der Komponente  |
 | molarer Anteil der Komponente  |
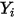 | Massenanteil der Komponente  |
Die vier Mengen sind wie folgt miteinander verbunden:

Gleichung 2.314
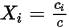
Gleichung 2.315
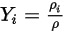
Gleichung 2.316
Dabei gilt:
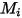 | Molekulargewicht der Komponente  |
 | Mischungsdichte |
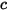 | Summe der molaren Konzentrationen aller Komponenten in einem System: |
und
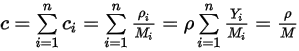
Gleichung 2.317
Dabei ist 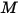 das Molekulargewicht der Mischung:
das Molekulargewicht der Mischung:
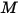 das Molekulargewicht der Mischung:
das Molekulargewicht der Mischung: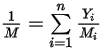
Gleichung 2.318
Die Gleichung 2.317 gibt an, dass bei einem massenanteilsgemittelten Molekulargewicht für die Mischung die Gleichung 2.314 ebenfalls für die Mischung der Komponenten des Typs  gilt.
gilt.
 gilt.
gilt.Außerdem muss gemäß den Definitionen in Gleichung 2.315 und Gleichung 2.316 die Summe der molaren Masse und der Massenanteile gleich 1 sein:

Gleichung 2.319
In CFA-Gleichungslösern erhalten Sie den Massenanteil der beliebigen Komponente 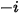 ,
, 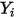 direkt durch das Lösen partieller Differentialtransportgleichungen. Die anderen Variablen,
direkt durch das Lösen partieller Differentialtransportgleichungen. Die anderen Variablen, 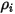 ,
, 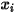 und
und 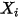 , sind Hilfsvariablen, die Sie für das Postprocessing verwenden.
, sind Hilfsvariablen, die Sie für das Postprocessing verwenden.
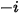 ,
, 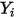 direkt durch das Lösen partieller Differentialtransportgleichungen. Die anderen Variablen,
direkt durch das Lösen partieller Differentialtransportgleichungen. Die anderen Variablen, 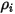 ,
, 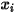 und
und 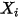 , sind Hilfsvariablen, die Sie für das Postprocessing verwenden.
, sind Hilfsvariablen, die Sie für das Postprocessing verwenden.Zugrunde liegende Gleichungen
In einem Mehrkomponenten-Fluss wird die Massenbewegung der Mischung unter Verwendung der Felder für die einzelne Geschwindigkeit, Druck, Temperatur und Turbulenz modelliert. Für das Mischen und Transportieren der chemischen Spezies hat jede Komponente eine eigene zugrunde liegende Gleichung für die Erhaltung der Masse. Der Einfluss mehrerer Komponenten auf den Massenfluss wird durch die Variation der Mischungseigenschaften wie Dichte, Viskosität, mit den Komponenteneigenschaften und den lokalen Massenanteilen spürbar.
• Massenanteilsgleichungen
Wenn es für den Mischungsfluss der Komponente 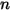 keine chemischen Reaktionen gibt, gilt für den Transport einer beliebigen Komponente des Typs
keine chemischen Reaktionen gibt, gilt für den Transport einer beliebigen Komponente des Typs  die folgende Gleichung:
die folgende Gleichung:
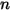 keine chemischen Reaktionen gibt, gilt für den Transport einer beliebigen Komponente des Typs
keine chemischen Reaktionen gibt, gilt für den Transport einer beliebigen Komponente des Typs  die folgende Gleichung:
die folgende Gleichung: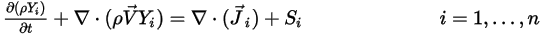
Gleichung 2.320
Dabei gilt:
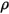 und und 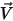 | Mischungsdichte und -geschwindigkeit |
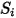 | jede beliebige benutzerdefinierte Quelle |
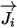 | Massendiffusionsterm |
Bei laminaren Strömungen sind der Geschwindigkeitsvektor 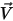 und der Massenanteil
und der Massenanteil 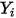 momentane Variablen. Bei turbulenten Strömungen sind diese Geschwindigkeitsvektoren Favre-gemittelte Mengen, da Mehrkomponenten-Flüsse als Flüsse mit variabler Dichte oder komprimierbare Flüsse betrachtet werden.
momentane Variablen. Bei turbulenten Strömungen sind diese Geschwindigkeitsvektoren Favre-gemittelte Mengen, da Mehrkomponenten-Flüsse als Flüsse mit variabler Dichte oder komprimierbare Flüsse betrachtet werden.
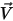 und der Massenanteil
und der Massenanteil 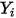 momentane Variablen. Bei turbulenten Strömungen sind diese Geschwindigkeitsvektoren Favre-gemittelte Mengen, da Mehrkomponenten-Flüsse als Flüsse mit variabler Dichte oder komprimierbare Flüsse betrachtet werden.
momentane Variablen. Bei turbulenten Strömungen sind diese Geschwindigkeitsvektoren Favre-gemittelte Mengen, da Mehrkomponenten-Flüsse als Flüsse mit variabler Dichte oder komprimierbare Flüsse betrachtet werden.In Gleichung 2.320 werden die Mischungsmengen und der Massendiffusionsterm wie folgt definiert:
◦ Mischungsdichte – Massen-gemittelter Wert aller Komponentendichten:
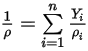
Gleichung 2.321
Bei einem Gemisch gasförmiger Spezies wird die Gemischdichte anhand des idealen Gasgesetzes auf der Basis des Molekulargewichts der Mischung 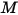 berechnet, das Sie mit der Gleichung 2.318 berechnen:
berechnet, das Sie mit der Gleichung 2.318 berechnen:
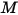 berechnet, das Sie mit der Gleichung 2.318 berechnen:
berechnet, das Sie mit der Gleichung 2.318 berechnen: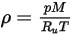
Gleichung 2.322
Dabei gilt:
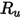 | Universelle Gaskonstante |
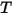 | Mischungstemperatur |
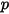 | Absoluter Druck |
Wenn Sie den Betriebsdruck (konstant) verwenden, wird die Gleichung 2.322 auf das sogenannte inkompressible ideale Gasgesetz reduziert. Dies ist eine angemessene Annahme für das Mischen und Transportieren von Spezies, bei denen der Manometerdruck im Vergleich zum Betriebsdruck häufig vernachlässigbar ist.
◦ Mischungsgeschwindigkeit – Masse-gemittelter Wert aller Komponentengeschwindigkeiten:
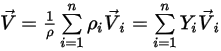
Gleichung 2.323
Da die Gleichung jedoch nur für eine einzelne Geschwindigkeit gelöst wird, gehen Sie davon aus, dass die Mischungsgeschwindigkeit und alle Komponentengeschwindigkeiten dieselben Werte haben.
◦ Massendiffusionsfluss – Der Massendiffusionsfluss der Komponente  besteht aus zwei Teilen: den laminaren und turbulenten Diffusionstermen, die ausgedrückt werden als:
besteht aus zwei Teilen: den laminaren und turbulenten Diffusionstermen, die ausgedrückt werden als:
 besteht aus zwei Teilen: den laminaren und turbulenten Diffusionstermen, die ausgedrückt werden als:
besteht aus zwei Teilen: den laminaren und turbulenten Diffusionstermen, die ausgedrückt werden als: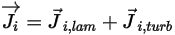
Gleichung 2.324
In Gleichung 2.324 ist 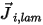 der laminare Diffusionsfluss der Komponente
der laminare Diffusionsfluss der Komponente  , der aufgrund von Gradienten von Konzentration und Temperatur entsteht. Standardmäßig verwendet Creo Flow Analysis die Verdünnungsapproximation oder das Fick-Gesetz, um die Massendiffusion aufgrund von Konzentrationsgradienten zu modellieren. Der laminare Diffusionsfluss hat die folgende Formel:
, der aufgrund von Gradienten von Konzentration und Temperatur entsteht. Standardmäßig verwendet Creo Flow Analysis die Verdünnungsapproximation oder das Fick-Gesetz, um die Massendiffusion aufgrund von Konzentrationsgradienten zu modellieren. Der laminare Diffusionsfluss hat die folgende Formel:
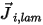 der laminare Diffusionsfluss der Komponente
der laminare Diffusionsfluss der Komponente  , der aufgrund von Gradienten von Konzentration und Temperatur entsteht. Standardmäßig verwendet Creo Flow Analysis die Verdünnungsapproximation oder das Fick-Gesetz, um die Massendiffusion aufgrund von Konzentrationsgradienten zu modellieren. Der laminare Diffusionsfluss hat die folgende Formel:
, der aufgrund von Gradienten von Konzentration und Temperatur entsteht. Standardmäßig verwendet Creo Flow Analysis die Verdünnungsapproximation oder das Fick-Gesetz, um die Massendiffusion aufgrund von Konzentrationsgradienten zu modellieren. Der laminare Diffusionsfluss hat die folgende Formel: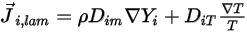
Gleichung 2.325
Dabei ist 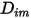 der Massendiffusionskoeffizient für die Komponente
der Massendiffusionskoeffizient für die Komponente  in der Mischung und
in der Mischung und 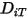 der Wärmediffusionskoeffizient (Soret).
der Wärmediffusionskoeffizient (Soret).
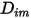 der Massendiffusionskoeffizient für die Komponente
der Massendiffusionskoeffizient für die Komponente  in der Mischung und
in der Mischung und 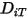 der Wärmediffusionskoeffizient (Soret).
der Wärmediffusionskoeffizient (Soret).Bei turbulenten Strömungen wird der Fluktuationsterm, der von der Favre-Mittelung der Advektion in Gleichung 2.320 abgeleitet wird, als turbulente Diffusion modelliert:
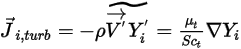
Gleichung 2.326
Dabei gilt:
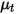 | Turbulente Viskosität |
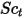 | Turbulente Schmidt-Zahl 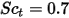 standardmäßig standardmäßig |
Die turbulente Diffusion überlagert im Allgemeinen die laminare Diffusion. Die Spezifikation detaillierter laminarer Diffusionseigenschaften in turbulenten Strömungen ist im Allgemeinen weniger wichtig als die ihrer turbulenten Gegenstücke.
Um die Kontinuitätsgleichung für den Mischungsfluss abzuleiten, addieren Sie alle Komponenten-Massenanteilsgleichungen und wenden Sie Gleichung 2.319 an:

Gleichung 2.327
Um die Gesamtmassenerhaltung des Mischungsflusses zu erfüllen, muss die Summe der Diffusionsterme für alle Komponenten 0 sein.
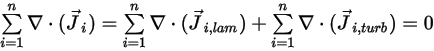
Gleichung 2.328
Aus Gleichung 2.319 und Gleichung 2.326 wird der turbulente Diffusionsterm immer bei 0 bestimmt. Daher wird für vollständig turbulente Strömungen normalerweise die Gleichung 2.328 als automatisch erfüllt betrachtet. Bei laminaren Strömungen oder wenn Sie die laminare Massendiffusion in turbulenten Strömungen nicht ignorieren können, wird die Gleichung 2.328 jedoch auf die folgende Form reduziert:
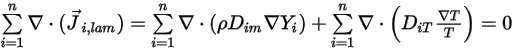
Gleichung 2.329
Um dann Gleichung 2.329 zu erfüllen, wenden Sie dann die zwei separaten Randbedingungen an:
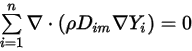
Gleichung 2.330
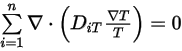
Gleichung 2.331
Die Kontinuitätsgleichung der Mehrkomponenten-Flüsse hat dann die endgültige Form:
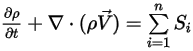
Gleichung 2.332
• Diffusionskoeffizienten
Um die Transportgleichung 2.320 für laminare Mehrkomponenten-Flüsse zu lösen, benötigen Sie den Massendiffusionskoeffizienten  und den Wärmediffusionskoeffizienten
und den Wärmediffusionskoeffizienten 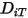 für jede Komponente in einer Mischung.
für jede Komponente in einer Mischung. 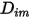 und
und  werden mithilfe folgender Methoden bestimmt:
werden mithilfe folgender Methoden bestimmt:
 und den Wärmediffusionskoeffizienten
und den Wärmediffusionskoeffizienten 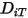 für jede Komponente in einer Mischung.
für jede Komponente in einer Mischung. 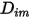 und
und  werden mithilfe folgender Methoden bestimmt:
werden mithilfe folgender Methoden bestimmt:◦ Massendiffusionskoeffizienten – Die Formel des Massendiffusionsflusses in laminaren Strömungen, Gleichung 2.325, ist streng gültig, wenn sich die Mischungszusammensetzung nicht ändert oder wenn 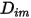 unabhängig von der Zusammensetzung ist. Dies ist eine akzeptable Approximation in verdünnten Mischungen, wenn
unabhängig von der Zusammensetzung ist. Dies ist eine akzeptable Approximation in verdünnten Mischungen, wenn  für alle Komponenten außer dem Trägergas sehr klein ist. Für nicht verdünnte Mischungen in laminaren Mehrkomponenten-Flüssen berechnen Sie
für alle Komponenten außer dem Trägergas sehr klein ist. Für nicht verdünnte Mischungen in laminaren Mehrkomponenten-Flüssen berechnen Sie 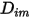 anhand folgender Formel:
anhand folgender Formel:
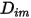 unabhängig von der Zusammensetzung ist. Dies ist eine akzeptable Approximation in verdünnten Mischungen, wenn
unabhängig von der Zusammensetzung ist. Dies ist eine akzeptable Approximation in verdünnten Mischungen, wenn  für alle Komponenten außer dem Trägergas sehr klein ist. Für nicht verdünnte Mischungen in laminaren Mehrkomponenten-Flüssen berechnen Sie
für alle Komponenten außer dem Trägergas sehr klein ist. Für nicht verdünnte Mischungen in laminaren Mehrkomponenten-Flüssen berechnen Sie 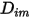 anhand folgender Formel:
anhand folgender Formel: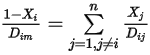
Gleichung 2.333
Dabei ist 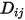 der binäre Massendiffusionskoeffizient der Komponente
der binäre Massendiffusionskoeffizient der Komponente  in der Komponente
in der Komponente 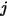 , den Sie angeben oder berechnen müssen.
, den Sie angeben oder berechnen müssen.
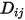 der binäre Massendiffusionskoeffizient der Komponente
der binäre Massendiffusionskoeffizient der Komponente  in der Komponente
in der Komponente 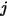 , den Sie angeben oder berechnen müssen.
, den Sie angeben oder berechnen müssen.◦ Angegebener Wert – Der binäre Massendiffusionskoeffizient 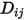 ist eine Konstante oder Funktion der Temperatur, wenn die Wärmeübertragung berücksichtigt wird. Sie können den Wert direkt angeben oder ihn aus der angegebenen Schmidt-Zahl abrufen:
ist eine Konstante oder Funktion der Temperatur, wenn die Wärmeübertragung berücksichtigt wird. Sie können den Wert direkt angeben oder ihn aus der angegebenen Schmidt-Zahl abrufen:
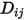 ist eine Konstante oder Funktion der Temperatur, wenn die Wärmeübertragung berücksichtigt wird. Sie können den Wert direkt angeben oder ihn aus der angegebenen Schmidt-Zahl abrufen:
ist eine Konstante oder Funktion der Temperatur, wenn die Wärmeübertragung berücksichtigt wird. Sie können den Wert direkt angeben oder ihn aus der angegebenen Schmidt-Zahl abrufen: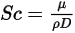
Gleichung 2.334
Dabei gilt:
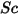 | Schmidt-Zahl |
Die Schmidt-Zahl ist als das Verhältnis der viskosen Diffusionsrate zur molekularen Diffusionsrate (Masse) definiert.
Wenn ein Wert oder eine Funktion der Temperatur für alle Komponenten gilt, wird die Gleichung 2.333 reduziert auf
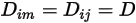
Gleichung 2.335
Gleichung 2.335 ist eine geeignete Approximation für die Modellierung einer verdünnten Mischung, wobei die Spezies in geringen Massenanteilen in einer Trägerflüssigkeit mit hoher Konzentration vorhanden ist. In solchen Fällen definieren Sie 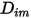 direkt als Konstante oder als Funktion der Temperatur.
direkt als Konstante oder als Funktion der Temperatur.
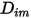 direkt als Konstante oder als Funktion der Temperatur.
direkt als Konstante oder als Funktion der Temperatur.Bei nicht verdünnten Mischungen, bei denen 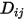 angegeben ist, verwenden Sie jedoch die Gleichung 2.333, um den einzelnen Massendiffusionskoeffizienten in der Mischung
angegeben ist, verwenden Sie jedoch die Gleichung 2.333, um den einzelnen Massendiffusionskoeffizienten in der Mischung  zu berechnen.
zu berechnen.
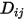 angegeben ist, verwenden Sie jedoch die Gleichung 2.333, um den einzelnen Massendiffusionskoeffizienten in der Mischung
angegeben ist, verwenden Sie jedoch die Gleichung 2.333, um den einzelnen Massendiffusionskoeffizienten in der Mischung  zu berechnen.
zu berechnen.◦ Kinetische Theorie – Für ein ideales Gas kann der binäre Massendiffusionskoeffizient  auch mithilfe der kinetischen Theorie ermittelt werden.
auch mithilfe der kinetischen Theorie ermittelt werden.
 auch mithilfe der kinetischen Theorie ermittelt werden.
auch mithilfe der kinetischen Theorie ermittelt werden.Referenzen: H. A. McGee, "Molecular Engineering", McGraw-Hill, New York, 1991.
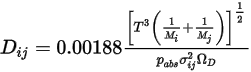
Gleichung 2.336
Dabei ist 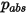 der absolute Druck und
der absolute Druck und 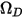 das Diffusions-Kollisionsintegral, das ein Maß für die Interaktion der Moleküle im System ist.
das Diffusions-Kollisionsintegral, das ein Maß für die Interaktion der Moleküle im System ist. 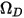 ist eine Funktion der Menge
ist eine Funktion der Menge 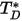 , definiert als:
, definiert als:
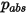 der absolute Druck und
der absolute Druck und 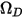 das Diffusions-Kollisionsintegral, das ein Maß für die Interaktion der Moleküle im System ist.
das Diffusions-Kollisionsintegral, das ein Maß für die Interaktion der Moleküle im System ist. 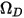 ist eine Funktion der Menge
ist eine Funktion der Menge 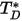 , definiert als:
, definiert als: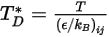
Gleichung 2.337
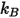 ist die Boltzmann-Konstante, die definiert ist als die universelle Gaskonstante
ist die Boltzmann-Konstante, die definiert ist als die universelle Gaskonstante 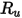 dividiert durch die Avogadro-Zahl.
dividiert durch die Avogadro-Zahl.  für die Mischung ist der geometrische Durchschnitt:
für die Mischung ist der geometrische Durchschnitt: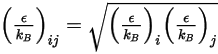
Gleichung 2.338
Für eine binäre Mischung wird 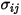 als arithmetischer Durchschnitt der einzelnen Werte
als arithmetischer Durchschnitt der einzelnen Werte 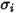 und
und  berechnet:
berechnet:
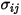 als arithmetischer Durchschnitt der einzelnen Werte
als arithmetischer Durchschnitt der einzelnen Werte 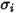 und
und  berechnet:
berechnet: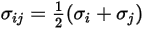
Gleichung 2.339
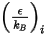 und
und 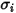 sind die Lennard-Jones-Parameter für die Komponente
sind die Lennard-Jones-Parameter für die Komponente  in der Mischung. Insbesondere ist
in der Mischung. Insbesondere ist 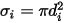 der Kollisionsquerschnitt des Kugelmoleküls mit dem Durchmesser
der Kollisionsquerschnitt des Kugelmoleküls mit dem Durchmesser 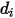 (beachten Sie, dass ein Molekül einen durch das Doppelte seines Durchmessers gegebenen Bereich bestreicht, da die Moleküle, mit denen es kollidiert, auch den Durchmesser
(beachten Sie, dass ein Molekül einen durch das Doppelte seines Durchmessers gegebenen Bereich bestreicht, da die Moleküle, mit denen es kollidiert, auch den Durchmesser  haben); und
haben); und 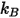 =1.38064852(79) ×10-23(J/K) ist die Boltzmann-Konstante.
=1.38064852(79) ×10-23(J/K) ist die Boltzmann-Konstante.In Creo Flow Analysis geben Sie den Durchmesser 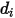 und die Energie
und die Energie  an, um die beiden Lennard-Jones-Parameter zu bestimmen.
an, um die beiden Lennard-Jones-Parameter zu bestimmen.
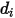 und die Energie
und die Energie  an, um die beiden Lennard-Jones-Parameter zu bestimmen.
an, um die beiden Lennard-Jones-Parameter zu bestimmen.◦ Wärmediffusionskoeffizienten 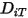 – Wärmediffusionskoeffizienten können als Konstanten, Polynomfunktionen der Temperatur, benutzerdefinierte Funktionen oder unter Verwendung des folgenden empirisch basierten, zusammensetzungsabhängigen Ausdrucks definiert sein, abgeleitet von:
– Wärmediffusionskoeffizienten können als Konstanten, Polynomfunktionen der Temperatur, benutzerdefinierte Funktionen oder unter Verwendung des folgenden empirisch basierten, zusammensetzungsabhängigen Ausdrucks definiert sein, abgeleitet von:
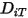 – Wärmediffusionskoeffizienten können als Konstanten, Polynomfunktionen der Temperatur, benutzerdefinierte Funktionen oder unter Verwendung des folgenden empirisch basierten, zusammensetzungsabhängigen Ausdrucks definiert sein, abgeleitet von:
– Wärmediffusionskoeffizienten können als Konstanten, Polynomfunktionen der Temperatur, benutzerdefinierte Funktionen oder unter Verwendung des folgenden empirisch basierten, zusammensetzungsabhängigen Ausdrucks definiert sein, abgeleitet von:Referenzen: K. K. Y. Kuo, "Principles of Combustion", John Wiley and Sons, New York, 1986.
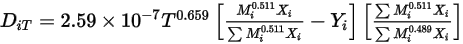
Gleichung 2.340
Diese Form des Wärmediffusionskoeffizienten bewirkt, dass schwere Moleküle weniger schnell diffundieren und leichte Moleküle schneller diffundieren, hin zu erwärmten Flächen.
• Impulsgleichungen
Mit den massengemittelten Eigenschaften und Geschwindigkeiten haben die Impulsgleichungen für die Mischung aller Komponenten denselben Ausdruck wie diejenigen für einzelne Flüssigkeitsflüsse:
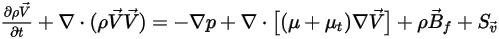
Gleichung 2.341
Dabei werden die Mischungsdichte und -geschwindigkeit anhand der Gleichung 2.321, der Gleichung 2.322 und der Gleichung 2.323 berechnet. Die turbulente Viskosität wird direkt aus den Turbulenzmodellen basierend auf dem Mischungsfluss berechnet, sodass ihr Wert von den Komponenten unabhängig ist. Die laminare Viskosität wird wie folgt berechnet:
◦ Massengemittelte laminare Viskosität – Für nicht-ideale Gasmischungen wird die Viskosität der Mischung basierend auf einem Massenanteilsdurchschnitt der Viskosität der reinen chemischen Spezies (Komponenten) berechnet:
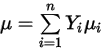
Gleichung 2.342
◦ Kinetische Theorie – Für ideale Gasmischungen wird die Viskosität der Mischung basierend auf der kinetischen Theorie berechnet. Für jede Komponente basiert die dynamische Viskosität auf der Boltzmann-Gleichung:
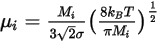
Gleichung 2.343
Für die Massendiffusivität benötigen Sie die Lennard-Jones-Parameter 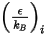 und
und 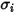 , um die Viskositäten der Gaskomponenten in einer Mischung zu berechnen.
, um die Viskositäten der Gaskomponenten in einer Mischung zu berechnen.
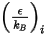 und
und 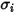 , um die Viskositäten der Gaskomponenten in einer Mischung zu berechnen.
, um die Viskositäten der Gaskomponenten in einer Mischung zu berechnen.Die Viskosität für die ideale Gasmischung wird dann wie folgt berechnet:
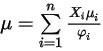
Gleichung 2.344
Dabei gilt:
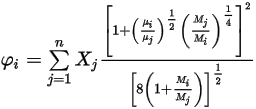
Gleichung 2.345
• Energiegleichung
Wie im Modul Wärme (Heat) beschrieben wird die Energiegleichung für die Mischung aller Komponenten wie folgt ausgedrückt:
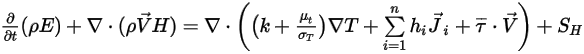
Gleichung 2.346
Dabei sind  und
und 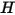 die gesamte innere Energie und die Gesamtenthalpie der Komponentenmischung
die gesamte innere Energie und die Gesamtenthalpie der Komponentenmischung 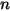 . Zusammen mit der mischungsspezifischen Wärme
. Zusammen mit der mischungsspezifischen Wärme  und der statischen Enthalpie
und der statischen Enthalpie 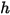 werden sie durch Massenmittelung der entsprechenden Werte der einzelnen Komponenten ermittelt:
werden sie durch Massenmittelung der entsprechenden Werte der einzelnen Komponenten ermittelt:
 und
und 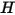 die gesamte innere Energie und die Gesamtenthalpie der Komponentenmischung
die gesamte innere Energie und die Gesamtenthalpie der Komponentenmischung 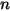 . Zusammen mit der mischungsspezifischen Wärme
. Zusammen mit der mischungsspezifischen Wärme  und der statischen Enthalpie
und der statischen Enthalpie 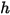 werden sie durch Massenmittelung der entsprechenden Werte der einzelnen Komponenten ermittelt:
werden sie durch Massenmittelung der entsprechenden Werte der einzelnen Komponenten ermittelt:◦ Massengemittelte Mischung – Wärmekapazität
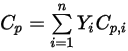
Gleichung 2.347
◦ Massegemittelte Mischungsenergie und -enthalpie
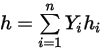
Gleichung 2.348
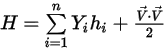
Gleichung 2.349

Gleichung 2.350
Die statische Enthalpie einer Komponente besteht aus zwei Teilen: der Standardzustands-Referenzenthalpie und der sensiblen Enthalpie. Bei Mehrkomponenten-Flüssen schließen Sie in die Berechnung von 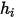 beide Teile der Enthalpie (Absolutwert oder Gesamtwert) ein.
beide Teile der Enthalpie (Absolutwert oder Gesamtwert) ein.
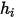 beide Teile der Enthalpie (Absolutwert oder Gesamtwert) ein.
beide Teile der Enthalpie (Absolutwert oder Gesamtwert) ein.In Gleichung 2.336 stellt der erste Ausdruck auf der rechten Seite die Diffusion der Energie dar. Er besteht aus drei Teilen: Wärmeleitung, Energietransport aufgrund der Diffusion der Spezies und viskose Erwärmung. Für die Wärmeleitung der Mischung wird dieser in derselben Weise modelliert wie in den einzelnen Flüssigkeitsflüssen. In Creo Flow Analysis wird die Wärmeleitfähigkeit der Mischung wie folgt berechnet:
◦ Massengemittelte Wärmeleitfähigkeit – Für nicht-ideale Gasmischungen wird die Wärmeleitfähigkeit der Mischung basierend auf einem einfachen Massenanteilsdurchschnitt der Wärmeleitfähigkeiten der reinen chemischen Spezies oder Komponenten berechnet:
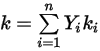
Gleichung 2.351
Dies ist die Standardmethode in Creo Flow Analysis.
◦ Kinetische Theorie – Für ideale Gasmischungen kann die Wärmeleitfähigkeit der Mischung basierend auf der kinetischen Theorie berechnet werden. Für jede Komponente hat die Wärmeleitfähigkeit die folgende Form:
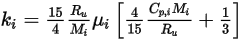
Gleichung 2.352
Dabei gilt:
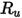 | Universelle Gaskonstante |
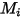 | Molekulargewicht |
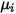 | angegebene oder berechnete Viskosität der Komponente |
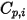 | angegebene oder berechnete spezifische Wärmekapazität der Komponente |
Beachten Sie, dass wie die laminare Viskosität 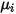 auch die spezifische Wärme
auch die spezifische Wärme 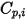 anhand der kinetischen Theorie ermittelt werden kann:
anhand der kinetischen Theorie ermittelt werden kann:
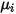 auch die spezifische Wärme
auch die spezifische Wärme 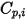 anhand der kinetischen Theorie ermittelt werden kann:
anhand der kinetischen Theorie ermittelt werden kann:
Gleichung 2.353
Dabei ist 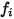 die Anzahl der Energiespeicherungsmodi (Freiheitsgrade) für die Gaskomponente
die Anzahl der Energiespeicherungsmodi (Freiheitsgrade) für die Gaskomponente  .
.
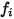 die Anzahl der Energiespeicherungsmodi (Freiheitsgrade) für die Gaskomponente
die Anzahl der Energiespeicherungsmodi (Freiheitsgrade) für die Gaskomponente  .
.Die Wärmeleitfähigkeit für die ideale Gasmischung wird dann wie folgt berechnet:
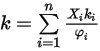
Gleichung 2.354
Dabei ist 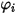 in Gleichung 2.335 ausgedrückt.
in Gleichung 2.335 ausgedrückt.
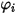 in Gleichung 2.335 ausgedrückt.
in Gleichung 2.335 ausgedrückt.Der zweite Diffusionsterm

Gleichung 2.355
stellt den Transport von Enthalpie durch die Diffusion der chemischen Spezies im Komponentenfluss 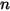 dar. Dieser Term kann einen erheblichen Einfluss auf das Enthalpie-Feld haben und sollte nicht vernachlässigt werden. Wenn die Lewis-Zahl (Verhältnis von Wärmeleitfähigkeit
dar. Dieser Term kann einen erheblichen Einfluss auf das Enthalpie-Feld haben und sollte nicht vernachlässigt werden. Wenn die Lewis-Zahl (Verhältnis von Wärmeleitfähigkeit 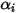 zu Masseleitfähigkeit
zu Masseleitfähigkeit 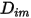 ):
):
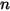 dar. Dieser Term kann einen erheblichen Einfluss auf das Enthalpie-Feld haben und sollte nicht vernachlässigt werden. Wenn die Lewis-Zahl (Verhältnis von Wärmeleitfähigkeit
dar. Dieser Term kann einen erheblichen Einfluss auf das Enthalpie-Feld haben und sollte nicht vernachlässigt werden. Wenn die Lewis-Zahl (Verhältnis von Wärmeleitfähigkeit 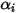 zu Masseleitfähigkeit
zu Masseleitfähigkeit 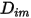 ):
):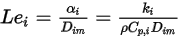
Gleichung 2.356
für eine Spezies nicht den Wert 1 hat, kann die Vernachlässigung dieses Terms erhebliche Fehler zum Ergebnis haben.
Der dritte Diffusionsterm ist der viskose Wärmebeitrag 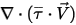 . Obwohl er auf dieselbe Weise wie beim einzelnen Flüssigkeitsfluss behandelt wird, berechnen Sie die Schubspannung
. Obwohl er auf dieselbe Weise wie beim einzelnen Flüssigkeitsfluss behandelt wird, berechnen Sie die Schubspannung 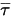 anhand der laminaren und turbulenten Viskositäten der Mischung. Der allgemeine Quellterm
anhand der laminaren und turbulenten Viskositäten der Mischung. Der allgemeine Quellterm 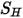 ist die gesamte externe oder Benutzer-Wärmequelle für alle Komponenten.
ist die gesamte externe oder Benutzer-Wärmequelle für alle Komponenten.
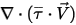 . Obwohl er auf dieselbe Weise wie beim einzelnen Flüssigkeitsfluss behandelt wird, berechnen Sie die Schubspannung
. Obwohl er auf dieselbe Weise wie beim einzelnen Flüssigkeitsfluss behandelt wird, berechnen Sie die Schubspannung 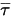 anhand der laminaren und turbulenten Viskositäten der Mischung. Der allgemeine Quellterm
anhand der laminaren und turbulenten Viskositäten der Mischung. Der allgemeine Quellterm 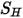 ist die gesamte externe oder Benutzer-Wärmequelle für alle Komponenten.
ist die gesamte externe oder Benutzer-Wärmequelle für alle Komponenten.• Turbulenzmodelle – Mit der Mischungsdichte 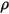 , der molekularen Viskosität
, der molekularen Viskosität 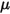 und der Geschwindigkeit
und der Geschwindigkeit 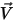 haben die Turbulenz-Modellierungsgleichungen sowohl in den Standard-k-ε- als auch in den RNG-k-ε-Modellen dieselben allgemeinen Formen wie bei den einzelne Flüssigkeits-Turbulenzmodellen. Diese werden im Modul Turbulenz (Turbulence) beschrieben. Die turbulente Viskosität für die Mischung
haben die Turbulenz-Modellierungsgleichungen sowohl in den Standard-k-ε- als auch in den RNG-k-ε-Modellen dieselben allgemeinen Formen wie bei den einzelne Flüssigkeits-Turbulenzmodellen. Diese werden im Modul Turbulenz (Turbulence) beschrieben. Die turbulente Viskosität für die Mischung 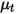 wird direkt aus dem Ausdruck berechnet:
wird direkt aus dem Ausdruck berechnet:
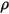 , der molekularen Viskosität
, der molekularen Viskosität 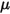 und der Geschwindigkeit
und der Geschwindigkeit 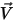 haben die Turbulenz-Modellierungsgleichungen sowohl in den Standard-k-ε- als auch in den RNG-k-ε-Modellen dieselben allgemeinen Formen wie bei den einzelne Flüssigkeits-Turbulenzmodellen. Diese werden im Modul Turbulenz (Turbulence) beschrieben. Die turbulente Viskosität für die Mischung
haben die Turbulenz-Modellierungsgleichungen sowohl in den Standard-k-ε- als auch in den RNG-k-ε-Modellen dieselben allgemeinen Formen wie bei den einzelne Flüssigkeits-Turbulenzmodellen. Diese werden im Modul Turbulenz (Turbulence) beschrieben. Die turbulente Viskosität für die Mischung 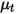 wird direkt aus dem Ausdruck berechnet:
wird direkt aus dem Ausdruck berechnet: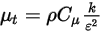
Gleichung 2.357
Auch wird die Produktion der kinetischen Turbulenzenergie auf der Basis der turbulenten Viskositäts- und Geschwindigkeitsgradienten der Mischung berechnet.
Modellierung von Mehrkomponenten-Berandungen
Im Mehrkomponenten-Fluss gelten für die Fluss-, Energie- und Turbulenzmodellierungsgleichungen dieselben Randbedingungen wie für die einphasigen Flüsse, die in den Modulen Flow, Heat und Turbulence beschrieben sind. Für die Massenanteile einer Komponente bestehen die Randbedingungen aus angegebenem Wert, angegebenem volumetrischem Fluss und/oder Gradient.
• n-Komponente – Einlassberandung
An einer Einlassberandung kann der Netto-Transport einer Komponente sowohl aus Konvektions- als auch aus Diffusionsbeiträgen bestehen. Die Konvektion wird durch den angegebenen Spezies-Massenanteil am Einlass bestimmt. Die Diffusion hängt vom Gradienten des berechneten Massenanteilsfelds ab. Bei sehr kleinen konvektiven Einlassgeschwindigkeiten kann aufgrund von Diffusion eine erhebliche Masse durch den Einlass gewonnen oder verloren gehen. Aus diesem Grund ist die Einlassdiffusion standardmäßig nicht eingeschlossen, kann jedoch als Option aktiviert werden.
◦ Angegebener Wert – Für den Komponentenfluss 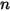 sind die Einlass-Massenanteile für
sind die Einlass-Massenanteile für 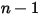 Komponenten vordefiniert, während der Massenanteil der Komponente
Komponenten vordefiniert, während der Massenanteil der Komponente 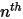 mit der physikalischen Bedingungsgleichung 2.319 ermittelt wird:
mit der physikalischen Bedingungsgleichung 2.319 ermittelt wird:
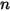 sind die Einlass-Massenanteile für
sind die Einlass-Massenanteile für 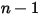 Komponenten vordefiniert, während der Massenanteil der Komponente
Komponenten vordefiniert, während der Massenanteil der Komponente 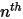 mit der physikalischen Bedingungsgleichung 2.319 ermittelt wird:
mit der physikalischen Bedingungsgleichung 2.319 ermittelt wird:
Gleichung 2.358
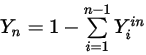
Gleichung 2.359
Außerdem darf der Massenanteil für keine der Komponente negativ sein.
◦ Angegebener volumetrischer Fluss – Unter der Annahme, dass 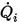 der vorab beschriebene volumetrische Eingangsfluss für die Komponente
der vorab beschriebene volumetrische Eingangsfluss für die Komponente  ist, wird der Massenstrom jeder Komponente
ist, wird der Massenstrom jeder Komponente 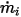 und der Gesamtmassenfluss am Einlass
und der Gesamtmassenfluss am Einlass 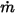 wie folgt ermittelt:
wie folgt ermittelt:
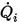 der vorab beschriebene volumetrische Eingangsfluss für die Komponente
der vorab beschriebene volumetrische Eingangsfluss für die Komponente  ist, wird der Massenstrom jeder Komponente
ist, wird der Massenstrom jeder Komponente 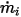 und der Gesamtmassenfluss am Einlass
und der Gesamtmassenfluss am Einlass 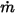 wie folgt ermittelt:
wie folgt ermittelt:
Gleichung 2.360
Dabei ist  die Einlassdichte der Komponente
die Einlassdichte der Komponente  .
.
 die Einlassdichte der Komponente
die Einlassdichte der Komponente  .
.Der Massenanteil wird per Definition wie folgt berechnet:
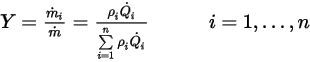
Gleichung 2.361
◦ Auslass-, Symmetrie-, Wand-Berandung – Für 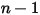 Komponenten gelten Null-Gradient-Bedingungen für alle Auslass-, Symmetrie- und Wandberandungen, während die
Komponenten gelten Null-Gradient-Bedingungen für alle Auslass-, Symmetrie- und Wandberandungen, während die 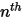 Phase mithilfe der physikalischen Randbedingung erreicht wird:
Phase mithilfe der physikalischen Randbedingung erreicht wird:
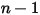 Komponenten gelten Null-Gradient-Bedingungen für alle Auslass-, Symmetrie- und Wandberandungen, während die
Komponenten gelten Null-Gradient-Bedingungen für alle Auslass-, Symmetrie- und Wandberandungen, während die 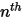 Phase mithilfe der physikalischen Randbedingung erreicht wird:
Phase mithilfe der physikalischen Randbedingung erreicht wird: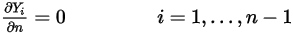
Gleichung 2.362
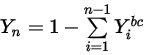
Gleichung 2.363
Dabei ist 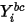 der Berandungswert, der aus der Gleichung 2.347 ermittelt wird.
der Berandungswert, der aus der Gleichung 2.347 ermittelt wird.
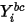 der Berandungswert, der aus der Gleichung 2.347 ermittelt wird.
der Berandungswert, der aus der Gleichung 2.347 ermittelt wird.Numerische Überlegungen
Die oben beschriebenen zugrunde liegenden Gleichungen, Turbulenzmodelle und Randbedingungen sind die Grundlage des Modells der Mehrkomponenten-Mischung. Ohne externe oder Benutzer-Quellterme und chemische Reaktionen sind diese ein geschlossenes Gleichungssystem, das Sie mit einem druckbasierten Finite-Volumen-Gleichungslöser numerisch lösen.
Die Massenanteil-Transportgleichungen werden für alle Komponenten gelöst. Um die physikalische Randbedingung zu erfüllen, werden die tatsächlichen Massenanteile um die Summe der gelösten Werte für alle Komponenten skaliert:

Gleichung 2.364
Dabei ist 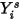 der Wert, der aus der Lösung der Gleichung 2.320 ermittelt wird. Der tatsächliche Massenanteil ist:
der Wert, der aus der Lösung der Gleichung 2.320 ermittelt wird. Der tatsächliche Massenanteil ist:
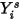 der Wert, der aus der Lösung der Gleichung 2.320 ermittelt wird. Der tatsächliche Massenanteil ist:
der Wert, der aus der Lösung der Gleichung 2.320 ermittelt wird. Der tatsächliche Massenanteil ist: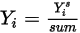
Gleichung 2.365