GDGL-Gleichungslöser
Die gewöhnlichen Differentialgleichungen (GDGLs) Gleichung 2.432 und Gleichung 2.444, die die 1-FG-Verschiebung und -Rotation der Berandungen bzw. Volumina steuern, werden in Creo Flow Analysis numerisch gelöst. Insbesondere werden zur Berechnung einer Bewegung und Verschiebung von Berandung und Volumen für die Neuvernetzung die folgenden Time-Marching-Schemata zur Integration in die GDGL-Gleichungen angenommen: explizite Gleichungslöser vom Typ Steif, Euler und Runge-Kutta.
Integration einer 1-FG-Translationsgleichung
Durch Substitution von Gleichung 2.434, Gleichung 2.435 und Gleichung 2.436 in Gleichung 2.432 und Gruppieren der expliziten Kraftterme in einem einzigen Term, kurz 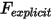 , wird die 1-FG-Translationsgleichung der Bewegung wie folgt umgeformt:
, wird die 1-FG-Translationsgleichung der Bewegung wie folgt umgeformt:
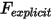 , wird die 1-FG-Translationsgleichung der Bewegung wie folgt umgeformt:
, wird die 1-FG-Translationsgleichung der Bewegung wie folgt umgeformt: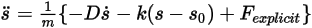
Gleichung 2.455
Dabei ist der explizit berechnete Kraftterm 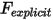 :
:
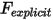 :
: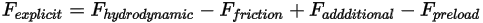
Gleichung 2.456
Bei gegebenen Anfangs- und Randbedingungen wird die Verschiebung des Volumenkörpers durch Integration von Gleichung 2.455 unter Verwendung expliziter Zeit-Marching-Schemata erlangt. Über den Zeitschritt  lauten die allgemeinen Formeln wie folgt:
lauten die allgemeinen Formeln wie folgt:
 lauten die allgemeinen Formeln wie folgt:
lauten die allgemeinen Formeln wie folgt:
Gleichung 2.457

Gleichung 2.458
Dabei ergibt die Summierung der Gewichtungsfaktoren den Wert 1:
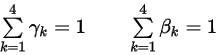
Gleichung 2.459
Mit der Auswahl von Gewichtungsfaktoren werden unterschiedliche Schemata abgeleitet. Beispielsweise folgen explizite Euler- und Runge-Kutta-Schemata:
• Expliziter Euler-Gleichungslöser (1. Ordnung)
Mit 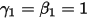 und
und 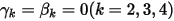 ist das explizite Euler-Schema Folgendes:
ist das explizite Euler-Schema Folgendes:
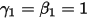 und
und 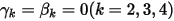 ist das explizite Euler-Schema Folgendes:
ist das explizite Euler-Schema Folgendes: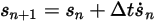
Gleichung 2.460
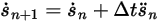
Gleichung 2.461
• Expliziter Runge-Kutta-Gleichungslöser
Die Runge-Kutta-Gleichungslöser sind explizite Schemata 2. und 4. Ordnung wie folgt:
◦ Schema zweiter Ordnung
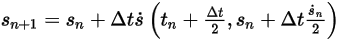
Gleichung 2.462
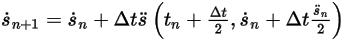
Gleichung 2.463
◦ Schema vierter Ordnung
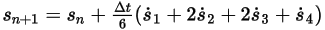
Gleichung 2.464
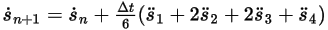
Gleichung 2.465
Dabei gilt:

Gleichung 2.466

Gleichung 2.467

Gleichung 2.468

Gleichung 2.469
• Steifer Gleichungslöser (Explizit)
Zusätzlich zu den standardmäßigen Euler- und Runge-Kutta-Schemata hat Creo Flow Analysis einen steifen Gleichungslöser entwickelt, um die GDGL-Gleichung für die 1-FG-Translation zu integrieren. Das ist die Standardmethode für dynamische Bewegungen von Volumenkörpern.
Integration einer 1-FG-Rotationsgleichung
Wie bei der Translation wird durch Substitution von Gleichung 2.446 und Gleichung 2.447 in Gleichung 2.444 und Gruppieren der expliziten Drehmomente in einem einzigen Term, kurz 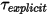 , die 1-FG-Rotationsgleichung der Bewegung, Gleichung 2.444 wie folgt umgeformt:
, die 1-FG-Rotationsgleichung der Bewegung, Gleichung 2.444 wie folgt umgeformt:
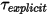 , die 1-FG-Rotationsgleichung der Bewegung, Gleichung 2.444 wie folgt umgeformt:
, die 1-FG-Rotationsgleichung der Bewegung, Gleichung 2.444 wie folgt umgeformt: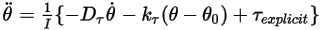
Gleichung 2.470
Dabei ist der explizit berechnete Drehmomentterm 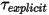 :
:
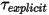 :
: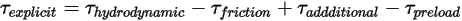
Gleichung 2.471
Bei gegebenen Anfangs- und Randbedingungen wird der Rotationswinkel durch Integration von Gleichung 2.470 unter Verwendung expliziter Zeit-Marching-Schemata erlangt. Über den Zeitschritt 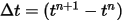 lauten die allgemeinen Formeln wie folgt:
lauten die allgemeinen Formeln wie folgt:
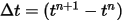 lauten die allgemeinen Formeln wie folgt:
lauten die allgemeinen Formeln wie folgt: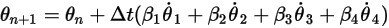
Gleichung 2.472
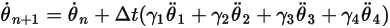
Gleichung 2.473
Dabei ergibt die Summierung der Gewichtungsfaktoren den Wert 1:
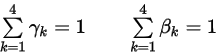
Gleichung 2.474
Mit der Auswahl von Gewichtungsfaktoren werden mühelos verschiedene numerische Schemata abgeleitet. Die expliziten Euler- und Runge-Kutta-Schemata sind wiederum unten angegeben:
• Expliziter Euler-Gleichungslöser (1. Ordnung)
Mit 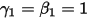 und
und  ist das explizite Euler-Schema Folgendes:
ist das explizite Euler-Schema Folgendes:
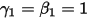 und
und  ist das explizite Euler-Schema Folgendes:
ist das explizite Euler-Schema Folgendes: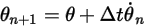
Gleichung 2.475

Gleichung 2.476
• Expliziter Runge-Kutta-Gleichungslöser
Die Runge-Kutta-Gleichungslöser sind explizite Schemata 2. und 4. Ordnung, die nachstehend angegeben sind:
◦ Schema zweiter Ordnung

Gleichung 2.477

Gleichung 2.478
◦ Schema vierter Ordnung
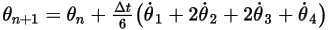
Gleichung 2.479
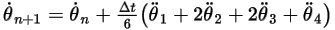
Gleichung 2.480
Dabei gilt:

Gleichung 2.481

Gleichung 2.482

Gleichung 2.483

Gleichung 2.484
• Steifer Gleichungslöser (Explizit)
Zusätzlich zu den standardmäßigen Euler- und Runge-Kutta-Schemata hat Creo Flow Analysis einen steifen Gleichungslöser entwickelt, um die Gleichung 2.444 der GDGL für die 1-FG-Rotation zu integrieren. Das ist die Standardmethode für dynamische Bewegungen von Volumenkörpern.