Cas de vérification : analyses modales
Analyse modale d'une poutre encastrée
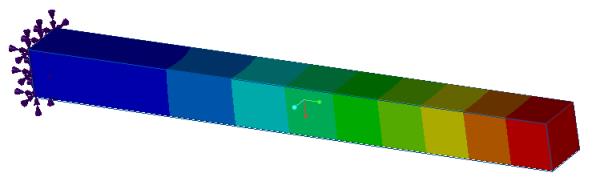
Enoncé du problème : prenez une poutre encastrée de longueur l, de largeur w et de hauteur h. Calculez les trois premiers modes de flexion et les fréquences naturelles. (Notez que les résultats de la simulation incluent les modes de flexion orthogonale, de torsion et axial. La comparaison des résultats compare les trois premiers modes de flexion d'une solution de forme fermée avec les résultats de simulation équivalents.)
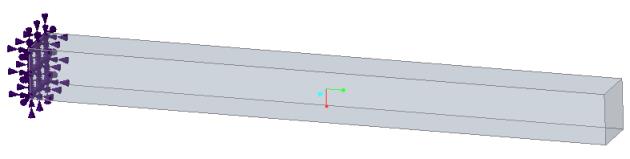
Références : W. T. Thompson, Theory of Vibration with Applications, 2nd Edition, Prentice-Hall, Inc.,Englewood Cliffs, NJ, 1981, pg. 220
Propriétés des matériaux | Propriétés géométriques |
|---|---|
Module de Young E = 70e9 Pa Coefficient de Poisson ν = 0.35 Densité ⍴ = 2700 kg/m^3 | l = 4 m w = 0.346 m h = 0.346 m |
Comparaison des résultats avec le curseur de qualité de simulation à sa position par défaut
Résultats | Cible | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Pourcentage d'erreur |
|---|---|---|---|---|---|
Mode de fréquence 1 (Hz) | 17.8 | 17.88 | 17.874 | 17.8 | 0 |
Mode de fréquence 3 (Hz) | 111.5 | 110.03 | 108.22 | 108.16 | 2.99 |
Mode de fréquence 6 (Hz) | 312.1 | 320.22 | 288.37 | 288.58 | 7.54 |
Comparaison des résultats pour Creo Ansys Simulation (maillage par défaut)
Résultats | Cible | Ansys AIM | Creo Ansys Simulation | Pourcentage d'erreur |
|---|---|---|---|---|
Mode de fréquence 1 (Hz) | 17.8 | 17.82 | 17.76 | 0.22 |
Mode de fréquence 3 (Hz) | 111.5 | 107.95 | 107.65 | 3.45 |
Mode de fréquence 6 (Hz) | 312.1 | 287.79 | 287.26 | 7.96 |
Analyse modale d'une poutre simplement appuyée
Enoncé du problème : déterminez la fréquence fondamentale d'une poutre simplement appuyée d'une longueur de 80 po et avec une section uniforme A = 4 po2, comme illustré ci-dessous.
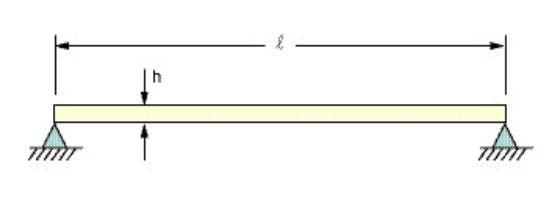
Références : W. T. Thompson, Vibration Theory and Applications, 2nd Printing, Prentice-Hall, Inc.,Englewood Cliffs, NJ, 1965, pg. 18, ex. 1.5-1
Propriétés des matériaux | Propriétés géométriques |
|---|---|
Module de Young E = 3e7 psi Coefficient de Poisson ν = 0.3 Densité ⍴ = 0.2836 lb/po^3 | l = 80 po w = 2 po h = 2 po |
Comparaison des résultats avec le curseur de qualité de simulation à sa position par défaut

(Support simple approximé avec une restriction de 0.125 sur les faces imprimées.)
Résultats | Cible | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Pourcentage d'erreur |
|---|---|---|---|---|---|
Mode de fréquence 1 (Hz) | 28.766 | 28.67 | 35.089 | 35.5 | 23.4 |
Comparaison des résultats pour Creo Ansys Simulation (maillage par défaut)
Résultats | Cible | Ansys AIM | Creo Ansys Simulation | Pourcentage d'erreur |
|---|---|---|---|---|
Mode de fréquence 1 (Hz) | 28.766 | 28.561 | 28.56 | 0.70 |
Analyse modale d'une plaque annulaire
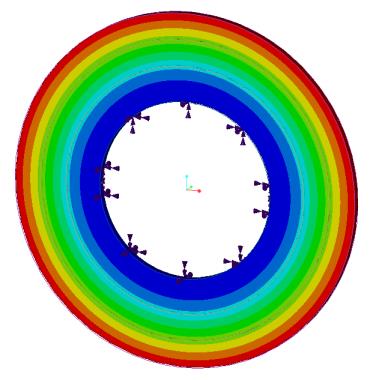
Enoncé du problème : un assemblage de trois plaques annulaires possède un support cylindrique (fixe dans les directions radiale, tangentielle et axiale) appliqué sur la surface cylindrique du trou. Déterminez les six premières fréquences naturelles.

Références : R. J. Blevins, Formula for Natural Frequency and Mode Shape, Van Nostrand Reinhold Company Inc., 1979, Table 11-2, Case 4, pg. 247
Propriétés des matériaux | Propriétés géométriques |
|---|---|
Module de Young E = 2.9008e7 psi Coefficient de Poisson ν = 0.3 Densité ⍴ = 0.28383 lb/po^3 | Diamètre intérieur de la plaque intérieure = 20 po Diamètre intérieur de la plaque médiane = 28 po Diamètre intérieur de la plaque extérieure = 34 po Diamètre extérieur de la plaque extérieure = 40 po Epaisseur de toutes les plaques = 1 po |
Comparaison des résultats avec le curseur de qualité de simulation à sa position par défaut
Résultats | Cible | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Pourcentage d'erreur |
|---|---|---|---|---|---|
Mode de fréquence 1 (Hz) | 310.9 | 310.92 | 322.84 | 327.6 | 5.36 |
Mode de fréquence 2 (Hz) | 318.1 | 316.37 | 328.56 | 333.3 | 4.79 |
Mode de fréquence 3 (Hz) | 318.1 | 316.50 | 328.59 | 333.4 | 4.80 |
Mode de fréquence 4 (Hz) | 351.6 | 347.80 | 359.83 | 364.6 | 3.70 |
Mode de fréquence 5 (Hz) | 351.6 | 347.94 | 360.74 | 365.9 | 4.08 |
Mode de fréquence 6 (Hz) | 442.4 | 436.54 | 449.31 | 454.7 | 2.77 |
Comparaison des résultats pour Creo Ansys Simulation (résolution de maillage par défaut)
Résultats | Cible | Ansys AIM | Creo Ansys Simulation | Pourcentage d'erreur |
|---|---|---|---|---|
Mode de fréquence 1 (Hz) | 310.9 | 309.64 | 311.55 | 0.21 |
Mode de fréquence 2 (Hz) | 318.1 | 314.99 | 316.91 | 0.38 |
Mode de fréquence 3 (Hz) | 318.1 | 315 | 317.09 | 0.32 |
Mode de fréquence 4 (Hz) | 351.6 | 345.97 | 348.03 | 1.01 |
Mode de fréquence 5 (Hz) | 351.6 | 345.98 | 349.18 | 0.97 |
Mode de fréquence 6 (Hz) | 442.4 | 434.15 | 436.20 | 1.04 |
Analyse modale d'une plaque rectangulaire
Enoncé du problème : prenez une plaque rectangulaire avec des supports fixes et les cotes de plaque suivantes : longueur = 6 po, largeur = 4 po et épaisseur = 0.063 po. Déterminez la fréquence naturelle et la déformée modale.
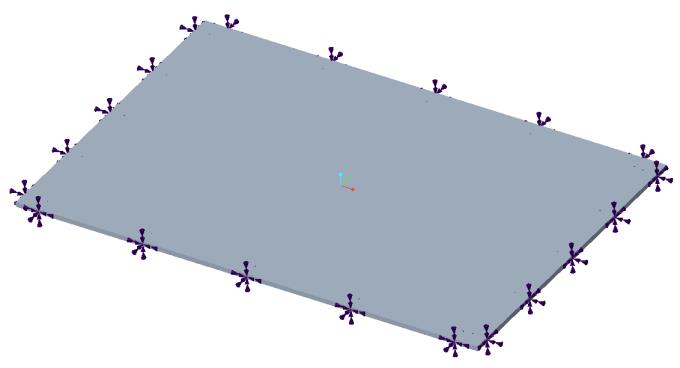
Références : R. Blevins, Formula for Natural Frequency and Mode Shape, Van Nostrand Reinhold Company Inc., 1979, Table 11-6
Propriétés des matériaux | Propriétés géométriques |
|---|---|
Module de Young E = 1.0e7 psi Coefficient de poisson ν = 0.33 Densité ⍴ = 0.1 lbm/po^3 | Longueur = 6 po Largeur = 4 po Epaisseur = 0.063 po |
Comparaison des résultats avec le curseur de qualité de simulation à sa position par défaut
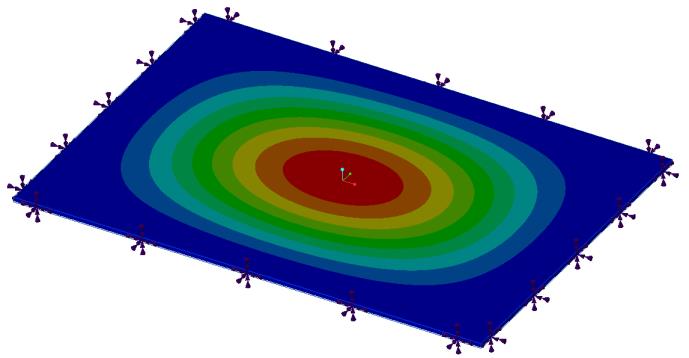
Résultats | Cible | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Pourcentage d'erreur |
|---|---|---|---|---|---|
Mode de fréquence 1 (Hz) | 1016 | 1019.35 | 1125.2 | 1125.16 | 10.74 |
Comparaison des résultats pour Creo Ansys Simulation (résolution de maillage par défaut)
Résultats | Cible | Ansys AIM | Creo Ansys Simulation | Pourcentage d'erreur |
|---|---|---|---|---|
Mode de fréquence 1 (Hz) | 1016 | 1020.6 | 1024.43 | 0.83 |