Définition des coefficients de Poisson selon Tsai
La relation entre les déformations, ( , etc.) et les contraintes (
, etc.) et les contraintes ( et similaire) s'écrit comme suit :
et similaire) s'écrit comme suit :
 , etc.) et les contraintes (
, etc.) et les contraintes ( et similaire) s'écrit comme suit :
et similaire) s'écrit comme suit :
La boîte de dialogue Définition de matériau (Material Definition) représente 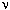 par Nu. par Nu. |
Dans l'expression ci-dessus, 1, 2 et 3 indiquent les trois directions de matériau principales. Dans un test de tension uniaxiale agissant dans la direction 1, les rapports entre les déformations normales transversales ( et
et  ) et la déformation normale longitudinale (
) et la déformation normale longitudinale ( ) sont donnés par :
) sont donnés par :
 et
et  ) et la déformation normale longitudinale (
) et la déformation normale longitudinale ( ) sont donnés par :
) sont donnés par : et
et 
D'autre part, la matrice d'élasticité étant symétrique, la relation suivante entre les coefficients de Poisson et les modules de Young est :

où i et j prennent les valeurs 1, 2 et 3.
Par conséquent, si  , alors
, alors 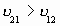 ,
,  et
et  .
.
 , alors
, alors 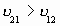 ,
,  et
et  .
.Les valeurs que vous entrez pour les coefficients de Poisson doivent faire en sorte que le déterminant de la matrice d'équations 6 X 6 ci-dessus soit positif.
Revenir à Coefficient de Poisson.