Physique des parois
Loi logarithmique de paroi :
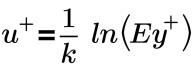
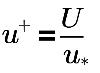
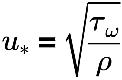
où,
u+ | vitesse adimensionnelle |
U | vitesse locale (centre de cellule) |
u* | vitesse de frottement |
τω | cisaillement de paroi |
ρ | vitesse du fluide |
E | coefficient constant |
k | constante de Von Karman (0.41) |
y+ | distance adimensionnelle entre la paroi et la cellule |
Fonctions et lois de paroi
Une fonction de paroi est requise pour modéliser le comportement des couches limites turbulentes à proximité de la paroi en l'absence de distributions de grille extrêmement denses au niveau d'une frontière (paroi) sans glissement. Du fait de l'existence d'un grand nombre de fonctions de paroi abondamment documentées, il est recommandé de rechercher la fonction qui convient pour une application spécifique. L'utilisation de la fonction de paroi est abordée dans la théorie de la couche limite. Source : Schlichting (Boundary Layer Theory, 6e édition, 1968 ISBN 07-055329-7).
La distance adimensionnelle y+ entre la paroi et un point de l'écoulement adjacent est définie sous la forme :
où,
vitesse de frottement | |
v | viscosité cinématique |
• sous-couche visqueuse 0 < y+< 5
• couche poreuse 5 < y+< 30
• couche inertielle 30 < y+< 200
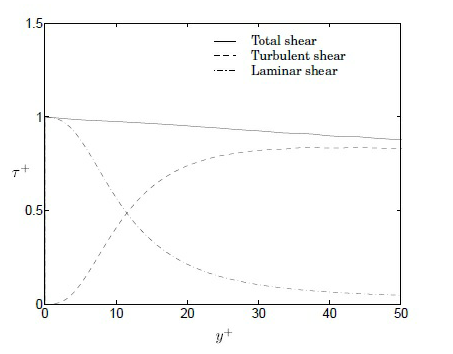
Plusieurs fonctions de paroi ont été développées pour prendre en charge les modèles de viscosité turbulente décrits ici :
• Standard (Standard) : modèle proposé par Launder et Spalding, définissant le profil de la vitesse moyenne turbulente à proximité de la paroi. La loi de paroi pour la distribution de la vitesse moyenne à l'aide de la fonction de paroi Standard (Standard) est formulée de la façon suivante :
Dans la sous-couche inertielle et la sous-couche visqueuse :
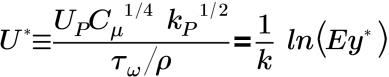
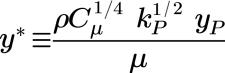
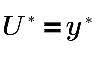
où,
k=0.4187 | constante de Von Karman |
E=9.793 | constante empirique |
UP | vitesse moyenne du fluide au point P |
kP | énergie cinétique de turbulence au point P |
yP | distance du point P à la paroi |
μ | viscosité dynamique du fluide |
La fonction de paroi Standard (Standard) est utilisée dans les applications industrielles et est également décrite dans la documentation relative aux écoulements de fluides. Elle repose sur l'hypothèse qu'il existe un équilibre local entre la production d'énergie cinétique turbulente K et le taux de dissipation d'énergie turbulente. La fonction de paroi Standard (Standard) offre les résultats les plus précis en matière de prévision des écoulements présentant de faibles gradients de pression, une absence de séparation et de recirculation, ainsi que des effets d'accélération ou de décélération négligeables.
• Nonequilibrium(Kim) : modèle proposé par Kim et définissant le profil de la vitesse moyenne turbulente à proximité de la paroi. La loi de paroi pour la distribution de la vitesse moyenne à l'aide de la fonction de paroi Nonequilibrium(Kim) est formulée de la façon suivante :
Dans la sous-couche inertielle :
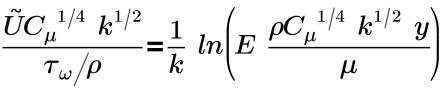
k=0.4187 | constante de Von Karman |
E=9.793 | constante empirique |
UP | vitesse moyenne du fluide au point P |
kP | vitesse moyenne de l'énergie cinétique turbulente du fluide au point P |
yP | distance du point P à la vitesse moyenne de l'énergie cinétique turbulente de paroi du fluide au point P |
μ | viscosité dynamique de la vitesse moyenne de l'énergie cinétique turbulente du fluide au point P |
Cμ | 0.09 |
La fonction de paroi Nonequilibrium(Kim) repose sur l'hypothèse que la production d'énergie cinétique turbulente diffère du taux de dissipation. La fonction de paroi Nonequilibrium(Kim) considère les effets de gradient de pression. Elle utilise un modèle à deux couches pour le traitement de la sous-couche visqueuse et de la couche inertielle pleinement turbulente. La fonction de paroi Nonequilibrium(Kim) applique un traitement de paroi amélioré qui utilise des fonctions de lissage dans la région poreuse de la paroi (3 < y+ < 10) afin d'assurer une transition harmonieuse entre la loi linéaire dans la sous-couche visqueuse et la loi logarithmique dans la sous-couche inertielle.
• Unified(Shih) : modèle proposé par Shih et définissant le profil de la vitesse moyenne turbulente dans l'ensemble de la couche limite. La loi de paroi pour la distribution de la vitesse moyenne à l'aide de la fonction de paroi Unified(Shih) est formulée de la façon suivante :
Dans l'ensemble de la couche limite où f1(Yτ+) et f2(Yρ+) sont des fonctions d'ajustement fragmentaires :
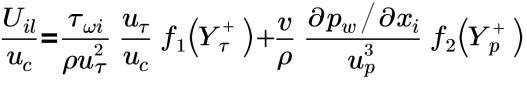
La fonction de paroi Unifiée (Shih) est valide dans la sous-couche visqueuse, la couche poreuse et la sous-couche inertielle (unifiée). La fonction de paroi Unifiée (Shih) offre de bons résultats pour les écoulements qui présentent des gradients de pression favorables ou défavorables, ainsi que pour les écoulements complexes limités par des parois avec accélération, décélération et recirculation. Cette fonction de paroi utilise un modèle à trois couches pour le traitement de la sous-couche visqueuse, de la couche poreuse et de la sous-couche inertielle.
Wall Roughness Model
Le modèle Modèle de rugosité de la paroi (Wall Roughness Model) se rapporte à la rugosité de la finition de surface sur une paroi.
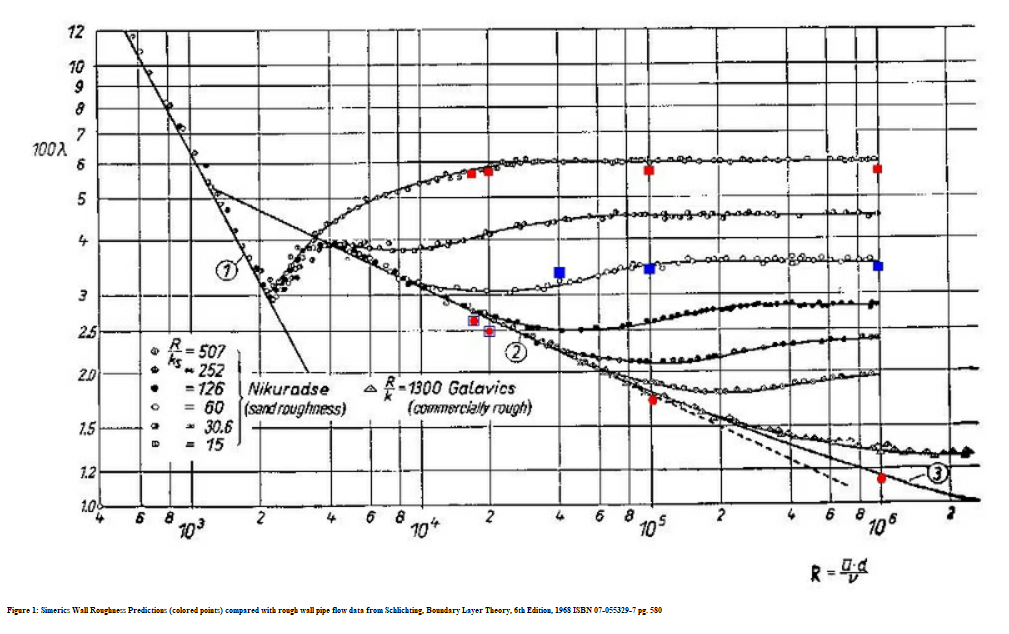
Comparaison des prévisions de rugosité des parois Creo Flow Analysis (points colorés) avec les données d'écoulement dans des conduites à paroi rugueuse. Source : Schlichting, Boundary Layer Theory, 6th Edition, 1968 ISBN 07-055329-7 pg. 580.