Physique
Cette rubrique décrit la théorie et la modélisation dans le module à l'aide des éléments suivants :
Equation de transport scalaire
Dans le module Espèces (Species), Creo Flow Analysis résout l'équation de transport d'un scalaire arbitraire défini par l'utilisateur. Pour un scalaire arbitraire,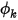 
, l'équation de transport générale a la forme suivante :
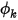, l'équation de transport générale a la forme suivante :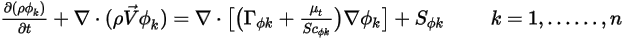
où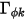 
, 
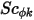et 
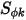correspondent respectivement au coefficient de diffusion spécifié par l'utilisateur, au nombre de Schmidt turbulent et au terme source pour le scalaire 
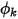. Ici, 
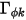est considéré comme isotrope. Il peut s'agir d'une valeur spécifiée directement ou d'une fonction définie par l'utilisateur. 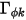est également indirectement déterminé par le biais d'un nombre de Schmidt spécifié, qui correspond à une valeur spécifiée ou à une fonction définie par l'utilisateur. Le nombre de Schmidt turbulent, 
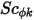, est une constante définie par l'utilisateur avec une valeur par défaut de 1. Le terme source 
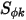peut être une constante ou une fonction définie par l'utilisateur sous la forme d'une source par volume ou de la source totale dans le domaine de calcul.
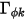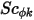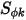, et correspondent respectivement au coefficient de diffusion spécifié par l'utilisateur, au nombre de Schmidt turbulent et au terme source pour le scalaire 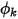. Ici, 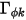est considéré comme isotrope. Il peut s'agir d'une valeur spécifiée directement ou d'une fonction définie par l'utilisateur. 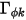est également indirectement déterminé par le biais d'un nombre de Schmidt spécifié, qui correspond à une valeur spécifiée ou à une fonction définie par l'utilisateur. Le nombre de Schmidt turbulent, 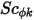, est une constante définie par l'utilisateur avec une valeur par défaut de 1. Le terme source 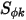peut être une constante ou une fonction définie par l'utilisateur sous la forme d'une source par volume ou de la source totale dans le domaine de calcul.Notez qu'en sélectionnant le module Espèces (Species), une seule équation scalaire est ajoutée. Pour les scalaires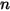 
, le module doit être sélectionné 
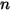fois et chaque espèce doit se voir affecter un nom différent.
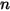, le module doit être sélectionné 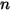fois et chaque espèce doit se voir affecter un nom différent.L'équation 2.376 est une équation scalaire générale. Elle peut être résolue seule pour un transport scalaire, ou en tant qu'ajout à certains ou à l'ensemble des modules standard. Etant donné que les termes de diffusion et de source sont déterminés par les entrées utilisateur de valeurs constantes ou de fonctions définies par l'utilisateur, l'équation de transport scalaire générale peut être utilisée pour développer de nouveaux modèles physiques tels que des modèles de turbulence et de combustion. Elle peut également être utilisée dans des formes réduites qui ne comportent que certains termes de l'équation. Des exemples sont proposés ci-après :
• Equations de Laplace et de Poisson
En mode de régime permanent, si le flux convectif n'est pas résolu ou reste constant, l'équation 2.376 est alors réduite à un problème de diffusion uniquement :
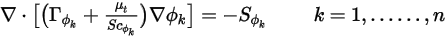
De même, si la diffusion turbulente est ignorée (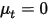
ou 
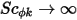) et que 
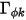est constante, l'équation 2.376 devient une équation de Poisson :
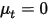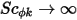ou ) et que 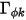est constante, l'équation 2.376 devient une équation de Poisson :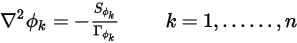
Et lorsque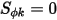 
, l'équation 2.376 scalaire est ajoutée à une équation de Laplace.
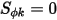, l'équation 2.376 scalaire est ajoutée à une équation de Laplace.Parmi de nombreuses applications, si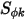 
est remplacé par la densité volumique de charge (
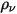) et que 
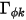correspond à la permittivité (
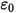), l'équation 2.376 peut être appliquée pour calculer le potentiel électrique (
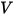) dans un champ électrique :
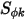est remplacé par la densité volumique de charge (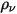) et que 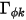correspond à la permittivité (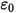), l'équation 2.376 peut être appliquée pour calculer le potentiel électrique (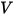) dans un champ électrique :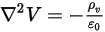
• Transport convectif
Sans le terme de diffusion (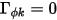
et 
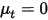ou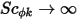 
), l'équation 2.376 est alors réduite comme suit :
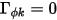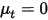et ou 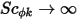), l'équation 2.376 est alors réduite comme suit :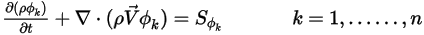
L'équation 2.376 peut être utilisée pour modéliser le transport des fractions volumiques de phase (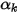
) dans les écoulements polyphasiques, dans lesquels les phases sont non miscibles (voir le module Polyphasique (Multiphase)) :
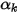) dans les écoulements polyphasiques, dans lesquels les phases sont non miscibles (voir le module Polyphasique (Multiphase)) :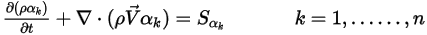
Lorsque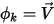 
et ⃗
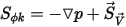, l'équation 2.376 représente les équations d'Euler pour les écoulements non visqueux :
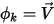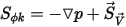et ⃗, l'équation 2.376 représente les équations d'Euler pour les écoulements non visqueux :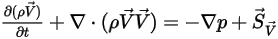
Conditions aux limites
Un scalaire défini par l'utilisateur représente une quantité physique quelconque. Par conséquent, les conditions aux limites ne sont pas définies comme les conditions aux limites d'écoulement. Par exemple, une frontière d'admission d'écoulement peut être interprétée très différemment pour le scalaire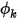 
. Par conséquent, pour l'équation de transport scalaire générale, vous pouvez appliquer tous les types de frontières définis pour les frontières physiques que vous sélectionnez.
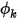. Par conséquent, pour l'équation de transport scalaire générale, vous pouvez appliquer tous les types de frontières définis pour les frontières physiques que vous sélectionnez.Si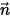 
est un vecteur d'unité normal à la surface frontière locale, l'expression générale du flux massique par unité de surface est la suivante :
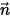est un vecteur d'unité normal à la surface frontière locale, l'expression générale du flux massique par unité de surface est la suivante :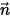si l'advection et la diffusion sont toutes les deux présentes à la frontière.
Pour le transport scalaire,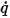 
représente le flux par unité de surface à la sortie ou à l'entrée du domaine physique à une frontière. Selon les applications, les conditions aux limites communes suivantes sont dérivées de cette formule générale :
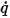représente le flux par unité de surface à la sortie ou à l'entrée du domaine physique à une frontière. Selon les applications, les conditions aux limites communes suivantes sont dérivées de cette formule générale :• Flux nul
Le flux par unité de surface sur (normal à) la frontière est spécifié sur zéro. Avec la condition de flux nul,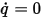 
, les flux convectif et de diffusion doivent être exactement identiques :
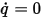, les flux convectif et de diffusion doivent être exactement identiques :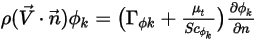
Cela signifie que si un terme est nul, l'autre terme doit l'être également. Par exemple, au niveau d'une frontière solide (paroi), la vitesse normale par rapport à la surface est égale à zéro,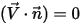 
, bien que 
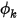ne soit pas nécessairement nul. Pour répondre à la contrainte de l'équation 2.376, le gradient du scalaire au niveau de la frontière doit être égal à zéro, 
.
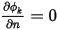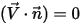, bien que 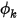ne soit pas nécessairement nul. Pour répondre à la contrainte de l'équation 2.376, le gradient du scalaire au niveau de la frontière doit être égal à zéro, 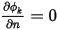.Dans Creo Flow Analysis, au niveau d'une paroi, le flux nul est la condition aux limites par défaut pour le scalaire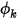 
.
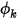.• Valeur spécifiée
La valeur spécifiée est une condition aux limites sous laquelle la valeur du scalaire à la frontière,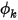 
, est déterminée directement par une valeur d'entrée utilisateur de 
:
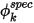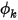, est déterminée directement par une valeur d'entrée utilisateur de :
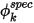Dans Creo Flow Analysis, au niveau d'une admission d'écoulement, la valeur constante spécifiée est la condition aux limites par défaut pour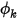 
.
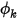.• Symétrie
Dans le cas d'une condition aux limites de symétrie, un gradient normal-frontière nul est appliqué pour le scalaire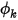 
:
:
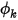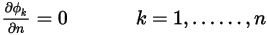
Dans Creo Flow Analysis, au niveau d'une frontière de symétrie d'écoulement, la symétrie est également la condition aux limites par défaut pour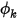 
.
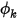.• Sortie
La sortie est utilisée comme condition aux limites au niveau d'une ouverture par laquelle l'écoulement est censé quitter le domaine ou y entrer. Pour une sortie de pression spécifiée, une résistance ou un condensateur dans l'écoulement, il s'agit de la condition par défaut pour le scalaire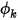 
.
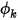.Au niveau d'une frontière de sortie, l'entrée requise est la valeur spécifiée pour le scalaire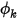 
. La condition aux limites réelle appliquée pour 
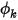dépend des conditions d'écoulement :
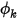. La condition aux limites réelle appliquée pour 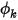dépend des conditions d'écoulement :◦ Ecoulement quittant le domaine : lorsque l'écoulement quitte le domaine de calcul à partir d'une sortie ou au niveau d'une entrée via un écoulement inversé, il est supposé que le gradient au niveau de la frontière est nul :
◦ Ecoulement entrant dans le domaine : lorsque l'écoulement entre dans le domaine de calcul à partir d'une entrée ou au niveau d'une sortie via un écoulement inversé, la valeur spécifiée s'applique pour la frontière :
• Flux convectif
Au niveau d'une frontière, le flux convectif de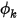 
par unité de surface (
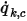) est déterminé en fonction de la valeur ambiante externe du scalaire (
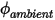) et d'un coefficient d'échange (
) :
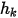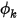par unité de surface (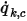) est déterminé en fonction de la valeur ambiante externe du scalaire (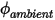) et d'un coefficient d'échange () :
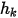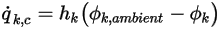
où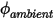 
et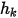 
sont des paramètres d'entrée utilisateur. Notez que le coefficient d'échange 
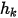a pour unité 
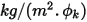. Dans le flux convectif connu 
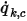, la valeur de frontière de 
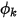est obtenue à partir de l'équation 2.376.
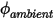et 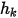sont des paramètres d'entrée utilisateur. Notez que le coefficient d'échange 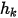a pour unité 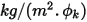. Dans le flux convectif connu 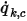, la valeur de frontière de 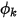est obtenue à partir de l'équation 2.376.• Flux scalaire spécifié
Dans cette condition aux limites, le flux du scalaire est spécifié de deux manières :
◦ Flux par zone : dans l'équation 2.376, le flux scalaire par unité de surface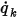 
est spécifié par une entrée utilisateur sous la forme d'une valeur constante ou d'une fonction définie par l'utilisateur :
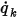est spécifié par une entrée utilisateur sous la forme d'une valeur constante ou d'une fonction définie par l'utilisateur :
Ensuite,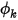 
est obtenu à partir de l'équation 2.376 en fonction des conditions d'écoulement.
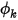est obtenu à partir de l'équation 2.376 en fonction des conditions d'écoulement.◦ Flux total : le flux scalaire total est connu via une entrée utilisateur sous la forme d'une valeur constante ou d'une fonction définie par l'utilisateur :
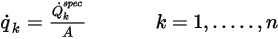
où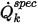 
correspond au flux scalaire total spécifié et 
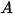à la zone de la frontière totale. Ensuite, 
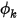est obtenu à partir de l'équation 2.376 en fonction des conditions d'écoulement.
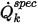correspond au flux scalaire total spécifié et 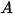à la zone de la frontière totale. Ensuite, 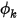est obtenu à partir de l'équation 2.376 en fonction des conditions d'écoulement.