Transfert de chaleur
Ecoulement laminaire à travers une conduite avec une densité de flux thermique uniforme
Enoncé du problème : l'écoulement laminaire 3D avec transfert de chaleur est modélisé dans une conduite à l'aide du module Chaleur (Heat). Le fluide pénètre dans la conduite à 300 K et une densité de flux thermique uniforme est appliquée au niveau de la paroi de la conduite.
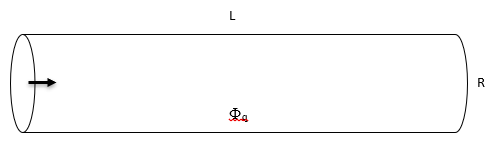
à : profil de vitesse entièrement développé à 300 K
Références : F.M. White. Fluid Mechanics. 3rd Edition. McGraw Hill Book Co. Inc., New York, NY, 1994.
Propriétés fluidiques | Propriétés géométriques | Conditions opérationnelles |
|---|---|---|
Densité = 13529 kg/m3 Viscosité = 0.001523 Pa-s Chaleur spécifique = 139.3 J/kg-K Conductivité = 8.54 W/m-K | R = 0.0025 m L = 0.1 m | Entrée = profil de vitesse entièrement développé à 300 K Sortie = 101325 Pa Փq = 5000 W/m2 |
Comparaison des résultats : chute de pression et température de sortie
Résultats | Solution analytique | Creo Flow Analysis | Pourcentage d'erreur |
|---|---|---|---|
Chute de pression (Pa) | 1 | 1.0054 | 0.54 |
Température de sortie (K) | 340 | 340.894 | 0.26 |
Convection naturelle dans un anneau concentrique
Enoncé du problème : la convection naturelle est modélisée dans un anneau concentrique à l'aide du module Chaleur (Heat). La température de la paroi interne de l'anneau concentrique est 50 K supérieure à celle de la paroi externe.
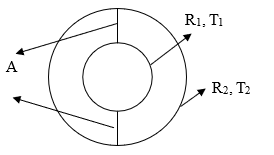
A = plan de symétrie
Références : T.H. Kuehn, R.J. Goldstein, "An Experimental Study of Natural Convection Heat Transfer in Concentric and Eccentric Horizontal Cylindrical Annuli", Journal of Heat Transfer, Vol 100, pp. 635-640, 1978.
Propriétés fluidiques | Propriétés géométriques | Conditions opérationnelles |
|---|---|---|
Densité = gaz idéal ou air Viscosité = 3.54822 x 10-5 Pa-s | Profil d'aile RAE 2822 Incidence = 2.31 degrés Hauteur de la soufflerie = 72 m Longueur de la soufflerie = 96 m | R1 = 0.0178 m T1 = 373 R2 = 0.4628 m T2 = 327 |
Résultat : contours de la température
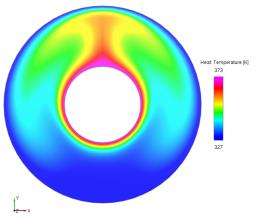
Comparaison des résultats : répartition de la température le long de la paroi de symétrie
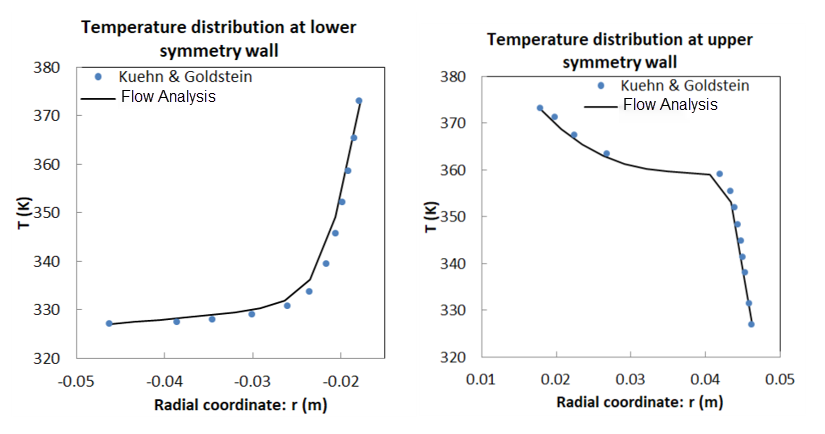
Comparaison des résultats : comparaison avec des données d'imagerie thermique

Conduction d'un bloc composite solide
Enoncé du problème : la conduction est modélisée dans un bloc composite solide composé de deux matières à l'aide du module Chaleur (Heat). Une densité de flux thermique définie au niveau de la paroi droite du bloc chauffe le système.
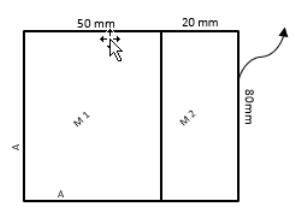
• A = paroi adiabatique
• M 1 = matière 1
◦ Densité = 2719 kg/m3
◦ Chaleur spécifique = 871 J/kg-K
◦ Conductivité thermique = 75 W/m-K
◦ Chaleur générée = 1.5*106W/m3
• M 2 = matière 2
◦ Densité = 8978 kg/m3
◦ Chaleur spécifique = 381 J/kg-K
◦ Conductivité thermique = 150 W/m-K
Références : F.P. Incropera, D.P. Dewitt. Fundamentals of Heat and Mass Transfer. 5th Edition, pg. 117, 2006.

Comparaison des résultats : température sur le bloc composite
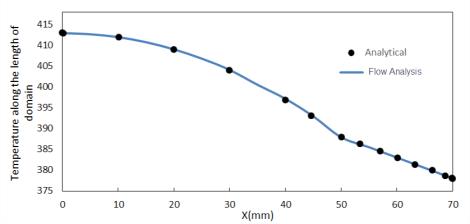
Conduction en régime transitoire dans une plaque semi-infinie
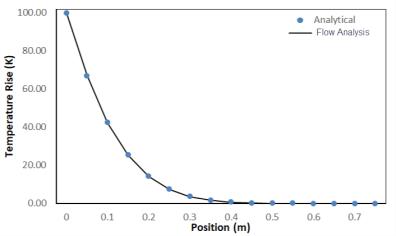
Enoncé du problème : une plaque semi-infinie est chauffée pendant 120 secondes par une densité de flux thermique uniforme définie au niveau de la paroi gauche de la plaque. La plaque est mesurée et les mesures obtenues sont comparées à la solution analytique.
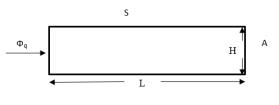
• S = symétrie
• A = paroi adiabatique
Références : F.P. Incropera, D.P. Dewitt, T.L. Bergman, A.S. Lavine, Introduction to Heat Transfer, 5th edition, Wiley and sons, 2007.
Propriétés solides | Propriétés géométriques | Conditions opérationnelles |
|---|---|---|
Densité = 8995.64 kg/m3 Chaleur spécifique = 381 J/kg-K Conductivité = 401 W/m-K | L = 0.75 m H = 0.1 m | Transitoire = 120 s Փq = 3 x 105 W/m2 Température initiale = 293 K |
Résultat : contours de la température

Comparaison des résultats : hausse de température sur la plaque