Exemple : Etudes de sensibilité, de faisabilité et d'optimisation
Résumé : cet exemple vous montre comment atteindre un objectif de conception à l'aide d'une analyse de sensibilité, d'une étude de faisabilité et d'une étude d'optimisation.
Problème : pour obtenir un équilibre optimal, le centre de gravité d'un vilebrequin doit coïncider avec son axe de rotation. L'axe de rotation du vilebrequin ne peut pas être modifié. Cependant, d'autres conditions de conception, telles que la largeur du vilebrequin, peuvent varier. Dans cette partie, vous souhaitez réduire la distance séparant l'axe de rotation et le centre de gravité tout en réduisant la masse de la pièce.
Solution : vous pouvez rechercher le centre de gravité et mesurer la distance qui le sépare de l'axe de rotation à l'aide d'une fonction d'analyse. Vous pouvez ensuite réaliser une analyse de sensibilité afin de rechercher les cotes qui ont le plus d'effets sur la position du centre de gravité. Enfin, vous pouvez effectuer une étude de faisabilité pour savoir s'il est possible de régler la distance entre le centre de gravité et l'axe de rotation sur zéro. S'il existe une solution, vous pouvez faire une étude d'optimisation pour réduire la masse du vilebrequin tout en maintenant le centre de gravité sur son axe.

1. Créez une fonction d'analyse afin de déterminer les propriétés massiques. Cliquez sur > > . Calculez la masse, créez un repère et un point de référence au niveau du centre de gravité ainsi que le paramètre MASS.
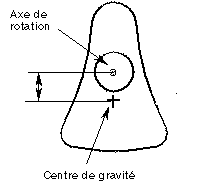
2. Créez une fonction d'analyse pour mesurer la distance séparant le point de référence au niveau du centre de gravité et l'axe de rotation. Comme résultat de cette mesure, vous pouvez créer un paramètre correspondant à cette distance.
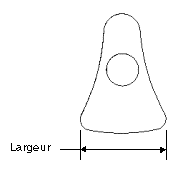
3. Effectuez une analyse de sensibilité pour connaître les effets de la variation de la cote de hauteur (width) sur la position du centre de gravité.
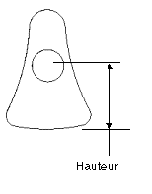
4. Effectuez une analyse de sensibilité pour connaître les effets de la variation de la cote de hauteur (height) sur la position du centre de gravité.
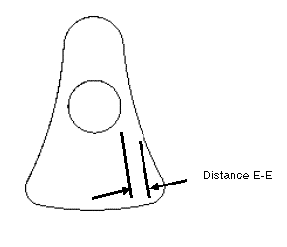
5. Créez une fonction d'analyse pour mesurer la distance séparant l'arbre et l'arête externe du profil de la pièce. Vous pouvez utiliser cette mesure pour définir les contraintes dans une étude de faisabilité. Créez des points de référence au début et à la fin de la ligne de distance. Dans la figure suivante, cette mesure s'affiche en tant que E-E distance.
6. Procédez à une étude de faisabilité pour déterminer s'il est possible de faire coïncider le centre de gravité et l'axe de rotation. Dans cette étude, vous faites varier les cotes de largeur, de hauteur et des rayons tout en conservant une certaine distance entre l'arbre de la pièce et l'arête externe du profil de la pièce (E-E distance).
7. Réalisez une étude d'optimisation pour réduire la masse tout en maintenant les contraintes indiquées à l'étape 6.