壁實體
壁的對數法則:
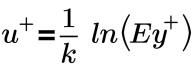
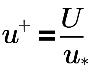
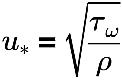
其中,
u+ | 無尺寸的速度 |
U | 局部 (儲存格中心) 速度 |
u* | 摩擦速度 |
τω | 壁剪切 |
ρ | 流體速度 |
E | 常數係數 |
k | 馮卡門 (Von Karman) 常數 (0.41) |
y+ | 無因次壁-格子距離 |
壁函數與法則
在非滑動邊界 (壁) 處不存在密度極高的格點分佈時,必須使用壁函數來為亂流邊界圖層建模壁附近的行為。文獻中存在各式各樣的壁函數,因此建議針對特定應用情況來研究何者為合適的壁函數。壁函數的用法是邊界圖層理論的主題 Schlichting (Boundary Layer Theory,第 6 版,1968 ISBN 07-055329-7)。
從壁到鄰接流體中某點的無尺寸距離 y+ 定義如下:
其中,
摩擦速度 | |
v | 運動黏度 |
• 黏性子圖層 0 < y+< 5
• 緩衝子圖層 5 < y+< 30
• 慣性子圖層 30 < y+< 200
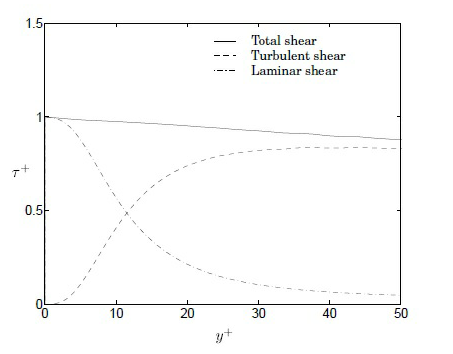
此處說明為支援亂流黏度模型所開發的數個壁函數:
• 「標準」(Standard) - 由 Launder 與 Spalding 提出,用來定義壁附近的亂流平均速度輪廓。用於平均速度分佈且使用「標準」(Standard) 壁函數的「壁法則」以公式表示如下:
在慣性子圖層與黏性子圖層中:
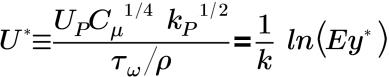
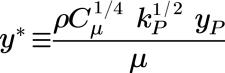
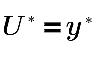
其中,
k=0.4187 | 馮卡門 (Von Karman) 常數 |
E=9.793 | 經驗常數 |
UP | 流體在點 P 處的平均速度 |
kP | 在點 P 處的流量動能 |
yP | 從點 P 到壁的距離 |
μ | 流體的動態黏度 |
「標準」(Standard) 壁函數用於工業應用程式,並在流體流動方向相關文件中有所說明。它的衍生基礎是假設亂流動能生產 K 和亂流能量消散率達到局部平衡態。所預測的流若具有小型壓力梯度、沒有分隔、沒有再循環,且可忽略加速或減速效果,則「標準」(Standard) 壁函數最為精確。
• 「非平衡態 (Kim)」(Nonequilibrium(Kim)) - 由 Kim 提出,用來定義壁附近的亂流平均速度輪廓。用於平均速度分佈且使用「非平衡態 (Kim)」(Nonequilibrium(Kim)) 壁函數的「壁法則」以公式表示如下:
在慣性子圖層中:
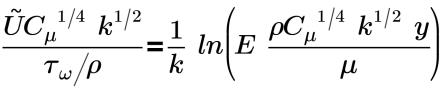
k=0.4187 | 馮卡門 (Von Karman) 常數 |
E=9.793 | 經驗常數 |
UP | 流體在點 P 處的平均速度 |
kP | 流體在點 P 處的亂流動能平均速度 |
yP | 從點 P 到壁的距離,流體在點 P 處之亂流動能平均速度 |
μ | 流體在點 P 處之流體亂流動能平均速度的動態黏度 |
Cμ | 0.09 |
「非平衡態 (Kim)」(Nonequilibrium(Kim)) 壁函數會假設亂流動能生產不等於消散率。「非平衡態 (Kim)」(Nonequilibrium(Kim)) 壁函數會將壓力梯度效果考慮進去。它會使用雙層式模型來處理黏性子圖層與完全亂流的慣性圖層。「非平衡態 (Kim)」(Nonequilibrium(Kim)) 壁函數會使用經過強化的壁處理方式,於壁緩衝區域 (3 < y+ < 10) 中使用混成函數,以便在黏性子圖層中的線性法則與慣性子圖層中的對數法則之間平順轉移。
• 「統一 (Shih)」(Unified(Shih)) - 由 Shih 提出,用來定義跨邊界圖層的亂流平均速度輪廓。用於平均速度分佈且使用「統一 (Shih)」(Unified(Shih)) 壁函數的「壁法則」以公式表示如下:
跨整個邊界圖層,其中 f1(Yτ+) 與 f2(Yρ+) 是分次擬合函數:
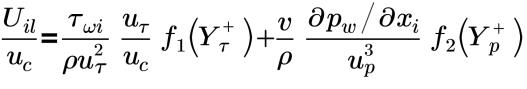
統一 (Shih) 壁函數在黏性子圖層、緩衝圖層和慣性子圖層 (統一) 中是有效的。對同時具備有利與不利壓力梯度的流和具備加速、減速和再循環且壁受到限制的複雜流動來說,統一 (Shih) 壁函數可發揮良好作用。這個壁函數會使用三層式模型來處理黏性子圖層、緩衝圖層和慣性子圖層。
壁粗糙度模型
「壁粗糙度模型」(Wall Roughness Model) 是指壁上曲面精度的粗糙度 (公尺)。
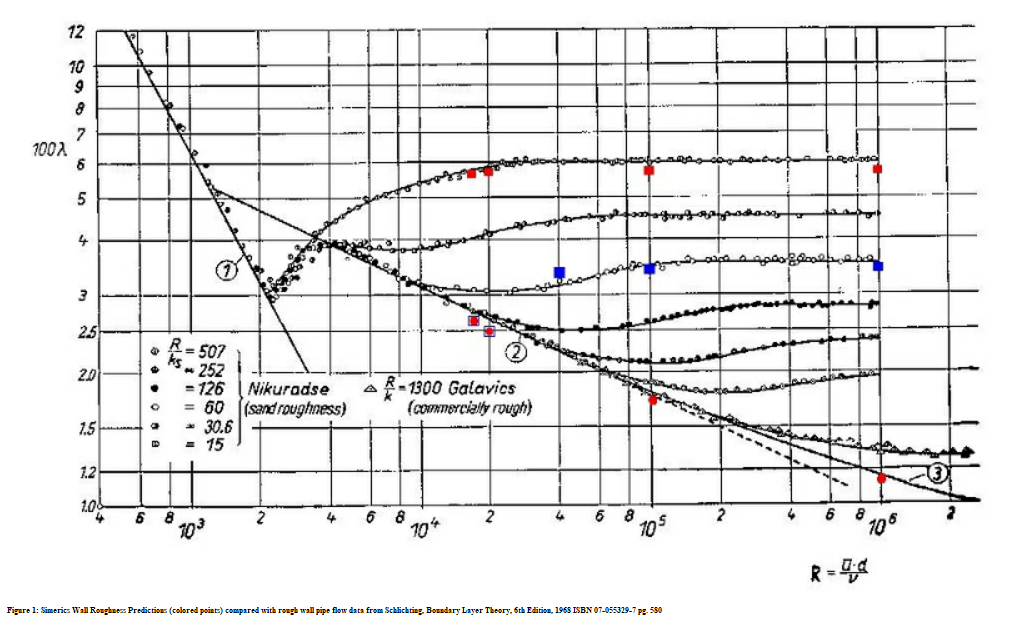
與粗略壁管路流量資料進行比較的 Creo Flow Analysis 壁粗糙度預測 (彩色點) Schlichting,Boundary Layer Theory,第 6 版,1968 ISBN 07-055329-7,頁580.