實體
欲建立流動流線,根據已求解的流場、指定的流線邊界和釋放條件追蹤無質量粒子的運動。
運動的粒子方程式
欲追蹤粒子運動,可對每個粒子的軌跡方程式進行分析或數字形式求解 (積分)。針對沿局部流場移動的無質量粒子,運動方程式重寫為:
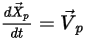
方程式 2.419
其中,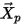 是粒子的位置向量;並且粒子速度
是粒子的位置向量;並且粒子速度 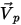 與位置
與位置 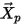 處的流動速度相同。流域中的
處的流動速度相同。流域中的 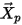 軌跡即為流動流線。
軌跡即為流動流線。
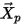 是粒子的位置向量;並且粒子速度
是粒子的位置向量;並且粒子速度 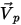 與位置
與位置 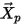 處的流動速度相同。流域中的
處的流動速度相同。流域中的 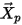 軌跡即為流動流線。
軌跡即為流動流線。邊界條件
Creo Flow Analysis 套用流線邊界條件,以決定邊界上流動流線的行為。當流線位於流域的邊界 (包括外部邊界與固體-流體介面) 時,例如壁或入口變異邊界,邊界上可能會發生下列情況之一:
• 流線即會被反射。
• 流線穿過邊界進入和/或退出。
• 流線穿過內部邊界區域,例如散逸或多孔跳躍面。
根據邊界上的流線行為,將流動邊界條件和流體-固體介面再次分為三種流線邊界條件:開放、對稱和壁。
• 開放 - 允許退出和/或進入計算域。開放邊界通常是流體流動的入口邊界或出口邊界。也可以套用於其他類型的流動邊界,例如壁與對稱。在開放邊界上,流線可根據粒子 (流動) 的速度方向退出或進入域。
將 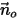 作為開放邊界的單位法向向量,該向量指向遠離計算域的方向。對於粒子邊界速度
作為開放邊界的單位法向向量,該向量指向遠離計算域的方向。對於粒子邊界速度 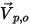 (與該點處的流動速度相同),在開放邊界上有下列流線條件:
(與該點處的流動速度相同),在開放邊界上有下列流線條件:
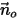 作為開放邊界的單位法向向量,該向量指向遠離計算域的方向。對於粒子邊界速度
作為開放邊界的單位法向向量,該向量指向遠離計算域的方向。對於粒子邊界速度 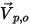 (與該點處的流動速度相同),在開放邊界上有下列流線條件:
(與該點處的流動速度相同),在開放邊界上有下列流線條件:◦ 如果 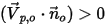 和速度向量
和速度向量 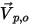 指向遠離計算域的方向。這表示粒子或流從邊界逸出。粒子在與邊界撞擊點處從流域中遺失。
指向遠離計算域的方向。這表示粒子或流從邊界逸出。粒子在與邊界撞擊點處從流域中遺失。
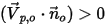 和速度向量
和速度向量 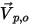 指向遠離計算域的方向。這表示粒子或流從邊界逸出。粒子在與邊界撞擊點處從流域中遺失。
指向遠離計算域的方向。這表示粒子或流從邊界逸出。粒子在與邊界撞擊點處從流域中遺失。◦ 如果 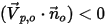 和速度向量
和速度向量 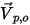 指向計算域的方向。這表示粒子或流從邊界進入域。此粒子與流入量一起從開放邊界釋放或注入流體流。粒子是與邊界撞擊點處流線計算的一部份。
指向計算域的方向。這表示粒子或流從邊界進入域。此粒子與流入量一起從開放邊界釋放或注入流體流。粒子是與邊界撞擊點處流線計算的一部份。
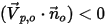 和速度向量
和速度向量 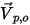 指向計算域的方向。這表示粒子或流從邊界進入域。此粒子與流入量一起從開放邊界釋放或注入流體流。粒子是與邊界撞擊點處流線計算的一部份。
指向計算域的方向。這表示粒子或流從邊界進入域。此粒子與流入量一起從開放邊界釋放或注入流體流。粒子是與邊界撞擊點處流線計算的一部份。• 對稱 - 流線會在邊界上反射。針對流線,對稱邊界通常會對應於流動對稱。它也可以是粒子釋放或逸出的位置,其方式與開放流線邊界相同。
將 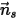 作為對稱邊界處點
作為對稱邊界處點 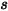 的法向對稱單位向量,其方向指向遠離對稱的計算域。此外,引入
的法向對稱單位向量,其方向指向遠離對稱的計算域。此外,引入 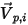 與
與 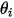 來指示對稱流線邊界上粒子撞擊速度 (局部流動速度) 的角度,如下圖所示。當粒子從對稱邊界反射時,切向速度保持相同,而法向速度分量僅變更正負號。從數學角度來看,粒子或流線對稱邊界條件表示為:
來指示對稱流線邊界上粒子撞擊速度 (局部流動速度) 的角度,如下圖所示。當粒子從對稱邊界反射時,切向速度保持相同,而法向速度分量僅變更正負號。從數學角度來看,粒子或流線對稱邊界條件表示為:
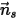 作為對稱邊界處點
作為對稱邊界處點 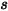 的法向對稱單位向量,其方向指向遠離對稱的計算域。此外,引入
的法向對稱單位向量,其方向指向遠離對稱的計算域。此外,引入 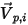 與
與 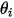 來指示對稱流線邊界上粒子撞擊速度 (局部流動速度) 的角度,如下圖所示。當粒子從對稱邊界反射時,切向速度保持相同,而法向速度分量僅變更正負號。從數學角度來看,粒子或流線對稱邊界條件表示為:
來指示對稱流線邊界上粒子撞擊速度 (局部流動速度) 的角度,如下圖所示。當粒子從對稱邊界反射時,切向速度保持相同,而法向速度分量僅變更正負號。從數學角度來看,粒子或流線對稱邊界條件表示為: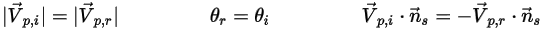
方程式 2.420
其中,
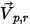 | 粒子反射速度 |
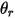 | 對稱邊界在點 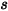 處的角度 處的角度 |
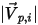 | 速度量值 |
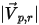 | 速度量值 |
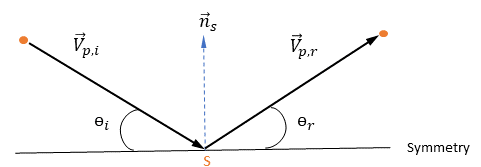
圖
由於無質量粒子以局部流動速度行進 (透過流動模擬獲得),因此在流線對稱邊界上對方程式 2.419 進行積分時,不需要邊界條件。
• 壁流線邊界
針對流線,壁流線邊界通常會對應於壁流動邊界。在流線壁邊界上,無質量粒子隨著流體流移動。由於局部流動速度 (即粒子速度) 是透過使用適當的近壁模型獲得,因此無需明確的壁邊界條件來求解方程式 2.419。
流線壁邊界可以是外部壁與流體-固體介面。針對開放流線邊界與對稱流線邊界,壁流線邊界也可以是粒子釋放的位置。
粒子釋放
從指定的流線邊界釋放的粒子可提供變異的初始條件和值。如同拉格朗日粒子追蹤中一樣,確定初始條件的程序涉及從邊界 (開放、對稱、壁和介面) 釋放粒子 (方向、位置、粒子數與分佈),以及為每個粒子指派屬性。
針對流線,每個無質量的粒子 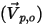 在其釋放位置
在其釋放位置 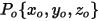 處的初始速度會自動設定為與局部流動速度
處的初始速度會自動設定為與局部流動速度 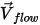 相同。在 Creo Flow Analysis 中,「釋放粒子」(Release Particle) 選項可控制流線粒子的釋放。
相同。在 Creo Flow Analysis 中,「釋放粒子」(Release Particle) 選項可控制流線粒子的釋放。
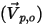 在其釋放位置
在其釋放位置 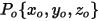 處的初始速度會自動設定為與局部流動速度
處的初始速度會自動設定為與局部流動速度 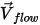 相同。在 Creo Flow Analysis 中,「釋放粒子」(Release Particle) 選項可控制流線粒子的釋放。
相同。在 Creo Flow Analysis 中,「釋放粒子」(Release Particle) 選項可控制流線粒子的釋放。流線動畫
欲建立流動流線並將其視覺化為曲線,將每個粒子的軌跡方程式方程式 2.419 進行數值求解或積分。針對流量解,粒子或流動速度值已知,可在動畫時間大小 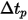 上對粒子速度進行前向尤拉積分來計算粒子位移:
上對粒子速度進行前向尤拉積分來計算粒子位移:
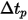 上對粒子速度進行前向尤拉積分來計算粒子位移:
上對粒子速度進行前向尤拉積分來計算粒子位移: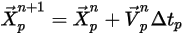
方程式 2.421
其中,
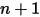 | 新值 |
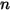 | 目前值 |
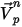 | 粒子 (局部流動) 速度 |
在第一個時間步長中,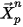 為釋放位置,
為釋放位置,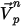 為釋放速度:
為釋放速度:
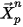 為釋放位置,
為釋放位置,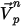 為釋放速度:
為釋放速度:
方程式 2.422
請注意,使用者指定的動畫時間步長 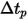 為一個實數乘數,用來對流線進行動畫顯示。值 1 表示動畫曲線與局部速度相同。
為一個實數乘數,用來對流線進行動畫顯示。值 1 表示動畫曲線與局部速度相同。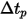 的值將曲線流動速度變更為局部流動速度的
的值將曲線流動速度變更為局部流動速度的 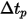 倍。
倍。
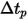 為一個實數乘數,用來對流線進行動畫顯示。值 1 表示動畫曲線與局部速度相同。
為一個實數乘數,用來對流線進行動畫顯示。值 1 表示動畫曲線與局部速度相同。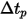 的值將曲線流動速度變更為局部流動速度的
的值將曲線流動速度變更為局部流動速度的 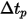 倍。
倍。此外,還可以指定「線條粗細」(Line Thickness) 的流線曲線的直徑。流線曲線的長度等於局部速度乘以動畫時間步長: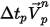 。此外,為防止流線追蹤程序花費太多計算時間來追蹤迴圈或停滯的流線,您可以引導使用者輸入的「最大積分步長」(Maximum Integral Steps) 來限制流線演算法追蹤流線的距離範圍。較小的值會縮短計算時間,但非常小的值可能會過早結束流線。
。此外,為防止流線追蹤程序花費太多計算時間來追蹤迴圈或停滯的流線,您可以引導使用者輸入的「最大積分步長」(Maximum Integral Steps) 來限制流線演算法追蹤流線的距離範圍。較小的值會縮短計算時間,但非常小的值可能會過早結束流線。
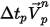 。此外,為防止流線追蹤程序花費太多計算時間來追蹤迴圈或停滯的流線,您可以引導使用者輸入的「最大積分步長」(Maximum Integral Steps) 來限制流線演算法追蹤流線的距離範圍。較小的值會縮短計算時間,但非常小的值可能會過早結束流線。
。此外,為防止流線追蹤程序花費太多計算時間來追蹤迴圈或停滯的流線,您可以引導使用者輸入的「最大積分步長」(Maximum Integral Steps) 來限制流線演算法追蹤流線的距離範圍。較小的值會縮短計算時間,但非常小的值可能會過早結束流線。