物理
針對多成分流動,您需要求解純量傳輸方程式以獲得混合物速度、壓力、溫度、亂流和其他實體數量。存在多個成分時,您必須求解其他方程式來確定成分在流體混合物內是如何傳輸的。
多個種類 (成分) 的描述
有多個不同但相關的變數來量化 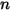 成分流動中成分
成分流動中成分  的內容:
的內容:
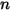 成分流動中成分
成分流動中成分  的內容:
的內容: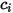 | 成分  的摩爾濃度 的摩爾濃度 |
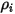 | 成分  的質量濃度 的質量濃度 |
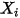 | 成分  的摩爾分數 的摩爾分數 |
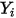 | 成分  的質量分數 的質量分數 |
四個數量相關聯,如下所示:
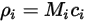
方程式 2.314
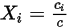
方程式 2.315
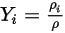
方程式 2.316
其中,
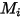 | 成分  的分子重量 的分子重量 |
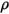 | 混合物密度 |
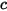 | 系統中所有成分摩爾濃度的總和: |
和
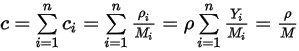
方程式 2.317
其中 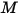 是混合物分子重量:
是混合物分子重量:
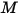 是混合物分子重量:
是混合物分子重量: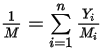
方程式 2.318
方程式 2.317 表示,若存在混合物的質量分數加權分子重量,則方程式 2.314 也適用於 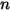 成分的混合物。
成分的混合物。
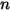 成分的混合物。
成分的混合物。此外,根據方程式 2.315 與方程式 2.316 中的定義,摩爾分數和質量分數的總和必須為 1:
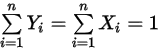
方程式 2.319
在 CFA 求解器中,可透過求解偏微分傳輸方程式,直接獲得任意成分 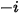 、
、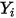 的質量分數。其他變數 (
的質量分數。其他變數 (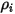 、
、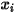 與
與 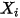 ) 是可用於後處理的輔助變數。
) 是可用於後處理的輔助變數。
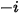 、
、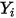 的質量分數。其他變數 (
的質量分數。其他變數 (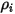 、
、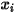 與
與 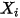 ) 是可用於後處理的輔助變數。
) 是可用於後處理的輔助變數。統御方程式
在多成分流動中,使用單一速度、壓力、溫度及亂流欄位對混合物的主體運動進行建模。針對化學物種的混合和傳輸,每個成分會有自己的質量守恆控制方程式。透過更改混合物內容 (如密度、黏度)、成分內容和局部質量分數,可以感知到多個成份對主體流動的影響。
• 質量分數方程式
針對 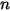 成分混合物流動,如果未發生化學反應,則任意元件
成分混合物流動,如果未發生化學反應,則任意元件  的傳輸由下列方程式控制:
的傳輸由下列方程式控制:
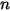 成分混合物流動,如果未發生化學反應,則任意元件
成分混合物流動,如果未發生化學反應,則任意元件  的傳輸由下列方程式控制:
的傳輸由下列方程式控制: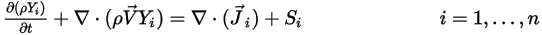
方程式 2.320
其中,
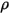 和 和 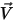 | 混合物密度與速度 |
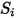 | 任何使用者定義的來源 |
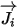 | 質量擴散項 |
針對層流,速度向量 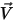 和質量分數
和質量分數 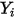 為即時變數。針對亂流,這些速度向量為 Favre 平均數量,因為多成分流被視為可變密度或可壓縮流。
為即時變數。針對亂流,這些速度向量為 Favre 平均數量,因為多成分流被視為可變密度或可壓縮流。
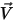 和質量分數
和質量分數 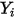 為即時變數。針對亂流,這些速度向量為 Favre 平均數量,因為多成分流被視為可變密度或可壓縮流。
為即時變數。針對亂流,這些速度向量為 Favre 平均數量,因為多成分流被視為可變密度或可壓縮流。在方程式 2.320 中,混合物數量和質量擴散項定義如下:
◦ 混合物密度 - 所有成分密度的質量平均值:

方程式 2.321
針對氣體種類的混合物,使用基於混合物分子重量 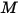 的理想氣體定律計算混合物密度,該重量可透過方程式 2.318 計算:
的理想氣體定律計算混合物密度,該重量可透過方程式 2.318 計算:
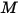 的理想氣體定律計算混合物密度,該重量可透過方程式 2.318 計算:
的理想氣體定律計算混合物密度,該重量可透過方程式 2.318 計算: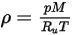
方程式 2.322
其中,
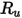 | 通用氣體常數 |
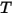 | 混合物溫度 |
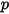 | 絕對壓力 |
如果您使用作業壓力 (恆定),方程式 2.322 會簡化為所謂的不可壓縮理想氣體定律。這是種類混合與傳輸的合理假設,其中表壓力與作業壓力相比通常可以忽略。
◦ 混合物速度 - 所有成分速度的質量平均值:
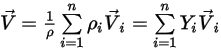
方程式 2.323
但是,由於只解得一個速度,因此可以假設混合物速度和所有成分速度具有相同值。
◦ 質量擴散通量 - 成分  的質量擴散通量由兩個部份組成:層流與亂流擴散項,其表示為:
的質量擴散通量由兩個部份組成:層流與亂流擴散項,其表示為:
 的質量擴散通量由兩個部份組成:層流與亂流擴散項,其表示為:
的質量擴散通量由兩個部份組成:層流與亂流擴散項,其表示為: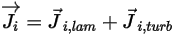
方程式 2.324
在方程式 2.324 中,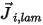 是由於濃度和溫度梯度而產生的成分
是由於濃度和溫度梯度而產生的成分  的層流擴散通量。依預設,Creo Flow Analysis 使用稀釋近似或菲克定律針對由於濃度梯度引起的質量擴散進行建模。層流擴散流有下列方程式:
的層流擴散通量。依預設,Creo Flow Analysis 使用稀釋近似或菲克定律針對由於濃度梯度引起的質量擴散進行建模。層流擴散流有下列方程式:
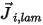 是由於濃度和溫度梯度而產生的成分
是由於濃度和溫度梯度而產生的成分  的層流擴散通量。依預設,Creo Flow Analysis 使用稀釋近似或菲克定律針對由於濃度梯度引起的質量擴散進行建模。層流擴散流有下列方程式:
的層流擴散通量。依預設,Creo Flow Analysis 使用稀釋近似或菲克定律針對由於濃度梯度引起的質量擴散進行建模。層流擴散流有下列方程式: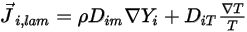
方程式 2.325
其中 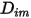 是混合物中成分
是混合物中成分  的質量擴散係數;
的質量擴散係數;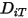 是熱 (Soret) 擴散係數。
是熱 (Soret) 擴散係數。
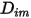 是混合物中成分
是混合物中成分  的質量擴散係數;
的質量擴散係數;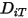 是熱 (Soret) 擴散係數。
是熱 (Soret) 擴散係數。針對亂流,透過對方程式 2.320 中的平流進行平均而衍生自此 Favre 的波動項,都會建模為亂流擴散:
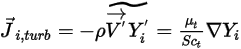
方程式 2.326
其中,
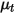 | 亂流黏度 |
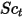 | 亂流施密特數 依預設為 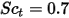 |
亂流擴散通常會壓倒層流擴散。亂流中詳細層流擴散內容的規格通常不如亂流所對應的重要。
欲衍生混合物流動的質量連續性方程式,請新增所有成分質量分數方程式並套用方程式 2.319:
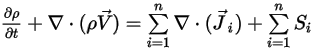
方程式 2.327
欲符合混合物流動的總質量守恆,所有成分擴散項的總和必須為零,
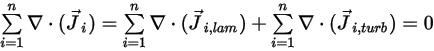
方程式 2.328
根據方程式 2.319 和方程式 2.326,亂流擴散項總是確定為零。因此,針對完全亂流,通常認爲方程式 2.328 自動符合。但是,針對層流,或當您不能忽略亂流中的層狀質量擴散時,方程式 2.328 會簡化為下列格式:
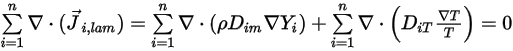
方程式 2.329
欲符合方程式 2.329,請套用兩個單獨的條件約束:
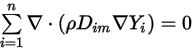
方程式 2.330
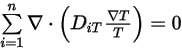
方程式 2.331
多成分流動的連續性方程式即會擁有最終格式:
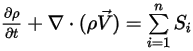
方程式 2.332
• 擴散係數
欲求解針對多成分層流的傳輸方程式 2.320,您需要混合物中每個成分的質量擴散係數 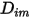 與熱擴散係數
與熱擴散係數 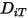 。決定
。決定 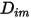 與
與 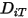 的方法如下:
的方法如下:
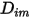 與熱擴散係數
與熱擴散係數 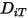 。決定
。決定 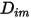 與
與 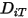 的方法如下:
的方法如下:◦ 質量擴散係數 - 當混合物構成未變更,或 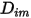 獨立於構成時,層流中質量擴散通量的公式方程式 2.325 嚴格有效。當
獨立於構成時,層流中質量擴散通量的公式方程式 2.325 嚴格有效。當 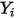 針對除載體氣體以外的所有成分非常小時,這是稀釋混合物中可接受的近似。針對多成分層流中的非稀釋混合物,您可從下列公式計算
針對除載體氣體以外的所有成分非常小時,這是稀釋混合物中可接受的近似。針對多成分層流中的非稀釋混合物,您可從下列公式計算 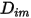 :
:
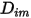 獨立於構成時,層流中質量擴散通量的公式方程式 2.325 嚴格有效。當
獨立於構成時,層流中質量擴散通量的公式方程式 2.325 嚴格有效。當 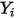 針對除載體氣體以外的所有成分非常小時,這是稀釋混合物中可接受的近似。針對多成分層流中的非稀釋混合物,您可從下列公式計算
針對除載體氣體以外的所有成分非常小時,這是稀釋混合物中可接受的近似。針對多成分層流中的非稀釋混合物,您可從下列公式計算 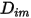 :
: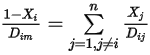
方程式 2.333
其中 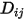 是成分
是成分 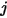 中成分
中成分  的二進位質量擴散係數,您需要指定或計算。
的二進位質量擴散係數,您需要指定或計算。
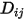 是成分
是成分 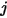 中成分
中成分  的二進位質量擴散係數,您需要指定或計算。
的二進位質量擴散係數,您需要指定或計算。◦ 指定的值 - 如果考慮熱轉換,則二進位質量擴散係數 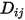 為是常數或溫度的函數。您可以直接指定值,也可以從指定的施密特數中獲得該值:
為是常數或溫度的函數。您可以直接指定值,也可以從指定的施密特數中獲得該值:
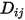 為是常數或溫度的函數。您可以直接指定值,也可以從指定的施密特數中獲得該值:
為是常數或溫度的函數。您可以直接指定值,也可以從指定的施密特數中獲得該值: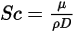
方程式 2.334
其中,
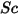 | 施密特數 |
施密特數會定義為黏性擴散率與分子 (質量) 擴散率的比。
如果一個值或一個溫度函數適用於所有成分,則方程式 2.333 會簡化為
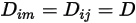
方程式 2.335
方程式 2.335 是針對稀釋混合物建模的適當近似,其中的種類以低質量分數存在於具有高濃度的載體流體流中。在這種情況下,可直接將 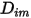 定義為常數或溫度的函數。
定義為常數或溫度的函數。
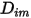 定義為常數或溫度的函數。
定義為常數或溫度的函數。但是,針對非稀釋混合物,若指定了 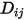 ,則可使用方程式 2.333 計算混合物
,則可使用方程式 2.333 計算混合物 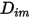 中的個別質量擴散係數。
中的個別質量擴散係數。
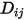 ,則可使用方程式 2.333 計算混合物
,則可使用方程式 2.333 計算混合物 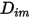 中的個別質量擴散係數。
中的個別質量擴散係數。◦ 動力理論 - 針對理想氣體,也可以使用動力理論 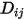 獲得二進位質量擴散係數。
獲得二進位質量擴散係數。
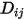 獲得二進位質量擴散係數。
獲得二進位質量擴散係數。參照:H. A. McGee,“Molecular Engineering”,McGraw-Hill,New York,1991。
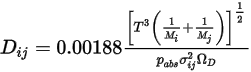
Equation 2.336
其中 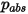 是絕對壓力,
是絕對壓力,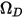 是擴散碰撞積分,即系統中分子互動的量測。
是擴散碰撞積分,即系統中分子互動的量測。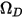 是數量
是數量 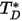 的函數,定義為:
的函數,定義為:
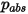 是絕對壓力,
是絕對壓力,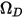 是擴散碰撞積分,即系統中分子互動的量測。
是擴散碰撞積分,即系統中分子互動的量測。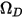 是數量
是數量 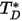 的函數,定義為:
的函數,定義為: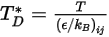
方程式 2.337
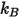 是波茲曼常數,定義為通用氣體常數
是波茲曼常數,定義為通用氣體常數 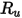 除以亞佛加厥數。混合物的
除以亞佛加厥數。混合物的 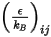 為幾何平均值:
為幾何平均值: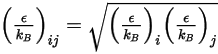
方程式 2.338
針對二進位混合物,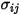 的計算方式為個別
的計算方式為個別 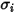 與
與 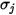 的算術平均值:
的算術平均值:
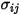 的計算方式為個別
的計算方式為個別 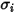 與
與 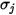 的算術平均值:
的算術平均值: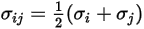
方程式 2.339
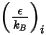 與
與 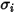 為混合物中成分
為混合物中成分  的 Lennard-Jones 參數。具體而言,
的 Lennard-Jones 參數。具體而言,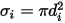 是球式分子的撞刀橫截面,直徑為
是球式分子的撞刀橫截面,直徑為 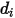 (請注意,分子掃描出一個兩倍直徑的區域,因爲其碰撞的分子也具有直徑
(請注意,分子掃描出一個兩倍直徑的區域,因爲其碰撞的分子也具有直徑 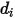 );並且
);並且 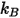 =1.38064852(79) × 10-23(J/K) 是波茲曼常數。
=1.38064852(79) × 10-23(J/K) 是波茲曼常數。在 Creo Flow Analysis 中,指定直徑 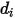 與能量
與能量 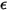 來確定兩個 Lennard-Jones 參數。
來確定兩個 Lennard-Jones 參數。
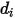 與能量
與能量 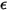 來確定兩個 Lennard-Jones 參數。
來確定兩個 Lennard-Jones 參數。◦ 熱擴散係數 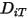 - 熱擴散係數可定義為常數、溫度的多項式函數、使用者定義函數,或使用衍生自下列內容的下列依賴於基礎組成的經驗運算式:
- 熱擴散係數可定義為常數、溫度的多項式函數、使用者定義函數,或使用衍生自下列內容的下列依賴於基礎組成的經驗運算式:
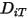 - 熱擴散係數可定義為常數、溫度的多項式函數、使用者定義函數,或使用衍生自下列內容的下列依賴於基礎組成的經驗運算式:
- 熱擴散係數可定義為常數、溫度的多項式函數、使用者定義函數,或使用衍生自下列內容的下列依賴於基礎組成的經驗運算式:參照:K. K. Y. Kuo, “Principles of Combustion”, John Wiley and Sons, New York, 1986。
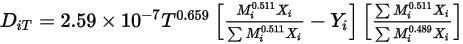
方程式 2.340
這種形式的熱擴散係數會導致重型分子向受熱曲面的擴散速度減慢,而輕量分子向受熱曲面的擴散速度加快。
• 動量方程式
使用質量加權內容與速度,所有成分混合物的動量方程式的運算式均與單一流體流動的相同:
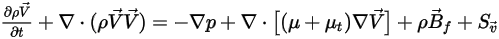
方程式 2.341
其中混合物密度與速度會使用方程式 2.321、方程式 2.322 及方程式 2.323 來計算。亂流黏度是根據混合物流動從亂流模型計算得到的,因此其值獨立於成分。針對層流黏度,其計算方法如下:
◦ 質量平均層流黏度 - 針對非理想氣體混合物,將根據純化學物種 (成分) 黏度的質量分數平均值來計算混合物黏度:
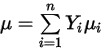
方程式 2.342
◦ 動力理論 - 針對理想氣體混合物,將根據動力理論計算混合物黏度。針對每個成分,動態黏度基於波茲曼方程式:
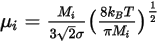
方程式 2.343
針對質量擴散,您需要 Lennard-Jones 參數、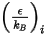 與
與 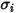 來計算混合物中氣體成分的黏度。
來計算混合物中氣體成分的黏度。
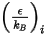 與
與 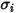 來計算混合物中氣體成分的黏度。
來計算混合物中氣體成分的黏度。理想氣體混合物的黏度則計算如下:
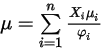
方程式 2.344
其中,
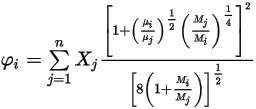
方程式 2.345
• 能量方程式
如熱模組中所述,所有成分混合物的能量方程式均表示為:
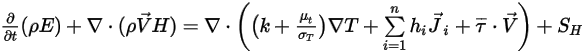
方程式 2.346
其中 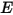 與
與 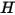 是
是 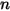 成分混合物的總內部能量和總焓。混合物特定熱
成分混合物的總內部能量和總焓。混合物特定熱 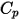 與靜態焓
與靜態焓 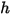 ,可透過計算每個成分對應值的質量平均值來獲得:
,可透過計算每個成分對應值的質量平均值來獲得:
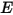 與
與 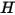 是
是 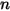 成分混合物的總內部能量和總焓。混合物特定熱
成分混合物的總內部能量和總焓。混合物特定熱 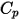 與靜態焓
與靜態焓 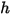 ,可透過計算每個成分對應值的質量平均值來獲得:
,可透過計算每個成分對應值的質量平均值來獲得:◦ 質量平均混合物熱容量
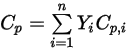
方程式 2.347
◦ 質量平均混合物能量與焓
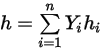
方程式 2.348
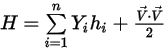
方程式 2.349
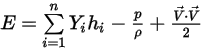
方程式 2.350
成分的靜態焓包括兩個部份:標準狀態參照焓與可感熱焓。針對多成分流動,計算 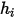 時應包括焓的兩個部份 (絕對值或總值)。
時應包括焓的兩個部份 (絕對值或總值)。
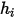 時應包括焓的兩個部份 (絕對值或總值)。
時應包括焓的兩個部份 (絕對值或總值)。在方程式 2.336 中,右側的第一項表示能量的擴散。它包括三個部份:熱傳導、由於類別擴散導致的能量傳輸,以及黏性加熱。針對混合物熱傳導,其建模方式與單一流體流動中的方式相同。在 Creo Flow Analysis 中,混合物熱導率計算如下:
◦ 質量平均熱導率 - 針對非理想氣體混合物,將根據純種類或成分熱導率的簡單質量分數平均值計算混合物熱導率:
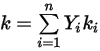
方程式 2.351
此為 Creo Flow Analysis 中的預設方法。
◦ 動力理論 - 針對理想氣體混合物,可根據動力理論計算混合物熱導率。針對每個成分,熱導率形式如下:
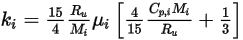
方程式 2.352
其中,
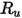 | 通用氣體常數 |
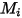 | 分子量 |
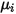 | 指定的或計算的成分黏度 |
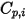 | 指定的或計算的成分比熱容量 |
請注意,作為層流黏度 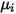 ,還可以使用動力理論獲得比熱
,還可以使用動力理論獲得比熱 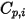 :
:
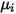 ,還可以使用動力理論獲得比熱
,還可以使用動力理論獲得比熱 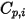 :
: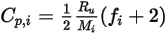
方程式 2.353
其中 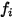 是氣體成分
是氣體成分  的能量儲存模式數 (自由度)。
的能量儲存模式數 (自由度)。
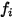 是氣體成分
是氣體成分  的能量儲存模式數 (自由度)。
的能量儲存模式數 (自由度)。理想氣體混合物的熱導率則計算如下:
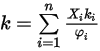
方程式 2.354
其中 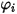 會在方程式 2.335 中表示。
會在方程式 2.335 中表示。
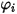 會在方程式 2.335 中表示。
會在方程式 2.335 中表示。第二個擴散項,
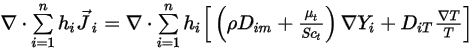
方程式 2.355
表示由於在 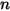 成分流動中化學物種的擴散而導致的焓傳輸。此項可對焓欄位有重大影響,並且不應忽略。當 Lewis 數 (熱擴散率
成分流動中化學物種的擴散而導致的焓傳輸。此項可對焓欄位有重大影響,並且不應忽略。當 Lewis 數 (熱擴散率 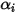 與質量擴散率
與質量擴散率 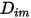 的比):
的比):
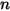 成分流動中化學物種的擴散而導致的焓傳輸。此項可對焓欄位有重大影響,並且不應忽略。當 Lewis 數 (熱擴散率
成分流動中化學物種的擴散而導致的焓傳輸。此項可對焓欄位有重大影響,並且不應忽略。當 Lewis 數 (熱擴散率 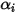 與質量擴散率
與質量擴散率 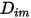 的比):
的比):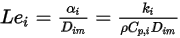
方程式 2.356
針對任何種類不是整體時,忽略此項可能會導致重大錯誤。
第三個擴散項是黏性加熱貢獻度 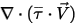 。雖然其處理方式與單一流體流動中的方式相同,但可使用混合物層流與亂流黏度來計算剪切應力
。雖然其處理方式與單一流體流動中的方式相同,但可使用混合物層流與亂流黏度來計算剪切應力 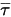 。一般源項
。一般源項 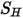 是所有成分的總外部或使用者熱源。
是所有成分的總外部或使用者熱源。
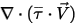 。雖然其處理方式與單一流體流動中的方式相同,但可使用混合物層流與亂流黏度來計算剪切應力
。雖然其處理方式與單一流體流動中的方式相同,但可使用混合物層流與亂流黏度來計算剪切應力 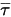 。一般源項
。一般源項 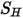 是所有成分的總外部或使用者熱源。
是所有成分的總外部或使用者熱源。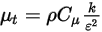
方程式 2.357
此外,亂流動能的結果也是根據混合物亂流黏度與速度梯度計算所得:
多成分邊界建模
• n-成分入口邊界
在入口邊界處,成分的淨傳輸可以包括對流與擴散貢獻度。對流取決於指定的入口種類質量分數。擴散取決於計算質量分數欄位的梯度。當對流入口速度極小時,可透過入口處的擴散獲取或失去實質質量。因此,依預設不包括入口擴散,但可以作爲選項啟用。
◦ 指定的值 - 針對 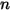 成分流動,
成分流動,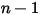 成分的入口質量分數會預先確定,而
成分的入口質量分數會預先確定,而 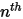 成分的質量分數是使用實體條件約束方程式 2.319 獲得的:
成分的質量分數是使用實體條件約束方程式 2.319 獲得的:
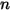 成分流動,
成分流動,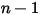 成分的入口質量分數會預先確定,而
成分的入口質量分數會預先確定,而 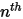 成分的質量分數是使用實體條件約束方程式 2.319 獲得的:
成分的質量分數是使用實體條件約束方程式 2.319 獲得的:
方程式 2.358
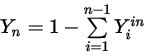
方程式 2.359
此外,每個成分的質量分數必須為非負數。
◦ 指定的體積通量 - 假設 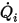 是成分
是成分  預先確定的入口體積通量,則每個成分的質量通量
預先確定的入口體積通量,則每個成分的質量通量 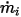 與入口處縂質量通量
與入口處縂質量通量 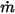 為:
為:
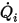 是成分
是成分  預先確定的入口體積通量,則每個成分的質量通量
預先確定的入口體積通量,則每個成分的質量通量 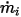 與入口處縂質量通量
與入口處縂質量通量 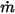 為:
為:
方程式 2.360
其中 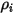 是成分
是成分  的入口密度。
的入口密度。
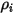 是成分
是成分  的入口密度。
的入口密度。根據定義,質量分數計算如下:
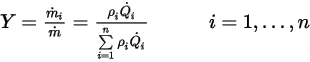
方程式 2.361
◦ 出口、對稱、壁邊界 - 針對 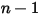 成分,零梯度條件適用於所有出口、對稱和壁邊界,而
成分,零梯度條件適用於所有出口、對稱和壁邊界,而 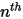 階段可使用實體條件約束獲得:
階段可使用實體條件約束獲得:
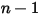 成分,零梯度條件適用於所有出口、對稱和壁邊界,而
成分,零梯度條件適用於所有出口、對稱和壁邊界,而 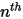 階段可使用實體條件約束獲得:
階段可使用實體條件約束獲得: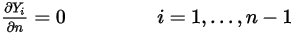
方程式 2.362
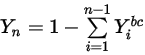
方程式 2.363
其中 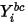 是從方程式 2.347 獲得的邊界值。
是從方程式 2.347 獲得的邊界值。
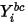 是從方程式 2.347 獲得的邊界值。
是從方程式 2.347 獲得的邊界值。數值考量
上述控制方程式、亂流模型與邊界條件形成了多成分混合模型的基礎。若沒有外部或使用者源項和化學反應,則它們是使用基於壓力的有限體積求解器以數值方式求解的封閉方程式系統。
求解所有成分的質量分數傳輸方程式。欲符合實體條件約束,實際質量分數會按所有成分求解值的總和進行縮放:

方程式 2.364
其中 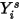 是透過求解方程式 2.320 獲得的值。實際質量分數為:
是透過求解方程式 2.320 獲得的值。實際質量分數為:
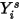 是透過求解方程式 2.320 獲得的值。實際質量分數為:
是透過求解方程式 2.320 獲得的值。實際質量分數為: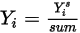
方程式 2.365
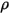 、分子黏度
、分子黏度 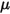 與速度
與速度 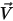 ,則
,則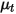 直接從下列運算式計算得來:
直接從下列運算式計算得來: