實體
本部份透過下列主題說明模組中涉及的理論知識與建模過程:
純量傳輸方程式
在「物種」(Species) 模組中,Creo Flow Analysis 可求解任意、使用者定義的純量傳輸方程式。對於任意純量 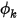 ,一般傳輸方程式的形式如下:
,一般傳輸方程式的形式如下:
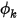 ,一般傳輸方程式的形式如下:
,一般傳輸方程式的形式如下: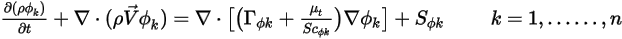
其中 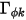 ,
,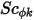 與
與 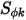 分別為使用者指定的擴散係數、亂流施密特數與純量
分別為使用者指定的擴散係數、亂流施密特數與純量  的來源項。在此,假設
的來源項。在此,假設 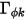 具有同向性。可以直接為其指定值或指定使用者定義的函數。
具有同向性。可以直接為其指定值或指定使用者定義的函數。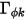 也可以透過指定的施密特數 (指定的值或使用者定義的函數) 間接確定。亂流施密特數
也可以透過指定的施密特數 (指定的值或使用者定義的函數) 間接確定。亂流施密特數 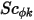 是使用者指定的常數,其預設值為 1。來源項
是使用者指定的常數,其預設值為 1。來源項 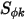 可以是常數或使用者定義的函數,在計算領域中採用單位體積來源或總來源的形式。
可以是常數或使用者定義的函數,在計算領域中採用單位體積來源或總來源的形式。
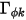 ,
,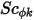 與
與 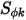 分別為使用者指定的擴散係數、亂流施密特數與純量
分別為使用者指定的擴散係數、亂流施密特數與純量  的來源項。在此,假設
的來源項。在此,假設 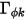 具有同向性。可以直接為其指定值或指定使用者定義的函數。
具有同向性。可以直接為其指定值或指定使用者定義的函數。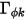 也可以透過指定的施密特數 (指定的值或使用者定義的函數) 間接確定。亂流施密特數
也可以透過指定的施密特數 (指定的值或使用者定義的函數) 間接確定。亂流施密特數 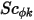 是使用者指定的常數,其預設值為 1。來源項
是使用者指定的常數,其預設值為 1。來源項 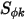 可以是常數或使用者定義的函數,在計算領域中採用單位體積來源或總來源的形式。
可以是常數或使用者定義的函數,在計算領域中採用單位體積來源或總來源的形式。請注意,透過選取模組物種只能新增一個純量方程式。對於 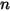 個純量的情況,必須執行
個純量的情況,必須執行 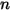 次模組選取動作,並為每個物種指派不同的名稱。
次模組選取動作,並為每個物種指派不同的名稱。
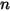 個純量的情況,必須執行
個純量的情況,必須執行 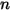 次模組選取動作,並為每個物種指派不同的名稱。
次模組選取動作,並為每個物種指派不同的名稱。方程式 2.376 是一般純量方程式。對於純量傳輸,該方程式可以單獨求解,或者,它也可以作為任何或所有標準模組的附加進行求解。由於擴散與來源項是由常數值或使用者定義的函數形式的使用者輸入所決定,因此一般純量傳輸方程式可用於開發新的物理模型,例如亂流與燃燒模型。此方程式也可以採用簡化形式,即方程式中僅包含某些項。如下面的範例所示:
• 普松與拉普拉斯方程式
在穩態模式下,如果對流通量未求解或保持恒定,則會將方程式 2.376 簡化為僅限於擴散的問題:
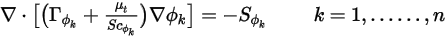
此外,如果略過亂流擴散 (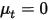 或
或 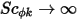 ),且
),且 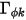 為常數,則方程式 2.376 會變成普松方程式:
為常數,則方程式 2.376 會變成普松方程式:
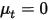 或
或 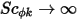 ),且
),且 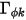 為常數,則方程式 2.376 會變成普松方程式:
為常數,則方程式 2.376 會變成普松方程式: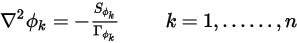
此外,當 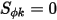 時,純量方程式 2.376 會進一步附加到拉普拉斯方程式。
時,純量方程式 2.376 會進一步附加到拉普拉斯方程式。
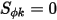 時,純量方程式 2.376 會進一步附加到拉普拉斯方程式。
時,純量方程式 2.376 會進一步附加到拉普拉斯方程式。在許多應用中,如果 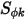 被體積塊電荷密度 (
被體積塊電荷密度 (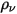 ) 取代,且
) 取代,且 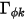 為介電常數 (
為介電常數 (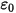 ),則可套用方程式 2.376 來計算電氣欄位中的電勢 (
),則可套用方程式 2.376 來計算電氣欄位中的電勢 (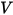 ):
):
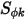 被體積塊電荷密度 (
被體積塊電荷密度 (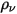 ) 取代,且
) 取代,且 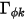 為介電常數 (
為介電常數 (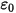 ),則可套用方程式 2.376 來計算電氣欄位中的電勢 (
),則可套用方程式 2.376 來計算電氣欄位中的電勢 (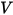 ):
):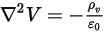
• 對流傳輸
若沒有擴散項 (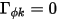 ,且
,且 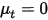 或
或 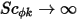 ),方程式 2.376 會簡化為:
),方程式 2.376 會簡化為:
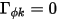 ,且
,且 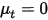 或
或 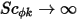 ),方程式 2.376 會簡化為:
),方程式 2.376 會簡化為: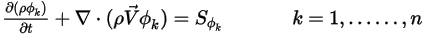
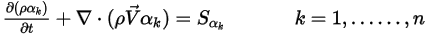
當 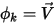 且 ⃗
且 ⃗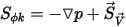 時,方程式 2.376 表示非黏性流動的歐拉方程式:
時,方程式 2.376 表示非黏性流動的歐拉方程式:
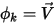 且 ⃗
且 ⃗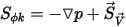 時,方程式 2.376 表示非黏性流動的歐拉方程式:
時,方程式 2.376 表示非黏性流動的歐拉方程式: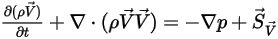
邊界條件
使用者定義的純量可以是任何物理量。因此,不會將邊界條件定義為流動邊界條件。例如,流動入口邊界可能完全是表示純量 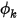 的其他內容。因此,對於一般純量傳輸方程式,您可以針對所選取的物理邊界套用所有已定義的邊界類型。
的其他內容。因此,對於一般純量傳輸方程式,您可以針對所選取的物理邊界套用所有已定義的邊界類型。
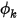 的其他內容。因此,對於一般純量傳輸方程式,您可以針對所選取的物理邊界套用所有已定義的邊界類型。
的其他內容。因此,對於一般純量傳輸方程式,您可以針對所選取的物理邊界套用所有已定義的邊界類型。如果 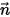 是法向於局部邊界曲面的單位向量,則每單位面積質量通量的一般運算式為:
是法向於局部邊界曲面的單位向量,則每單位面積質量通量的一般運算式為:
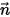 是法向於局部邊界曲面的單位向量,則每單位面積質量通量的一般運算式為:
是法向於局部邊界曲面的單位向量,則每單位面積質量通量的一般運算式為: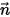
如果邊界上既存在平流又存在擴散。
對於純量傳輸,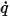 表示在邊界處離開或進入物理領域的每單位面積通量。根據應用而定,可以由此一般公式導出下列通用邊界條件:
表示在邊界處離開或進入物理領域的每單位面積通量。根據應用而定,可以由此一般公式導出下列通用邊界條件:
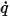 表示在邊界處離開或進入物理領域的每單位面積通量。根據應用而定,可以由此一般公式導出下列通用邊界條件:
表示在邊界處離開或進入物理領域的每單位面積通量。根據應用而定,可以由此一般公式導出下列通用邊界條件:• 零通量
將跨 (法向於) 邊界的每單位面積通量指定為零。若條件為零通量,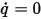 ,則對流與擴散通量必須完全相抵:
,則對流與擴散通量必須完全相抵:
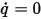 ,則對流與擴散通量必須完全相抵:
,則對流與擴散通量必須完全相抵: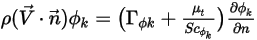
這表示如果一個項目等於零,則另一個項目也必須為零。例如,在實體 (壁) 邊界上,曲面的法向速度為零,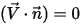 ,但
,但 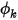 不一定為零。為了滿足方程式 2.376 中的條件約束,邊界處的純量梯度必須為零
不一定為零。為了滿足方程式 2.376 中的條件約束,邊界處的純量梯度必須為零 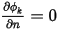 。
。
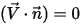 ,但
,但 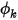 不一定為零。為了滿足方程式 2.376 中的條件約束,邊界處的純量梯度必須為零
不一定為零。為了滿足方程式 2.376 中的條件約束,邊界處的純量梯度必須為零 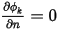 。
。在 Creo Flow Analysis 中,壁上的零通量是純量 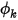 的預設邊界條件。
的預設邊界條件。
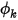 的預設邊界條件。
的預設邊界條件。• 指定的值
指定的值是一種邊界條件,其中該邊界條件下邊界處的純量值 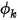 直接由使用者輸入值
直接由使用者輸入值 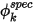 決定:
決定:
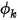 直接由使用者輸入值
直接由使用者輸入值 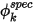 決定:
決定:
在 Creo Flow Analysis 中,在流動入口處指定的常數值是 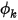 的預設邊界條件。
的預設邊界條件。
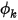 的預設邊界條件。
的預設邊界條件。• 對稱
針對對稱邊界條件,將針對純量 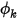 使用零法向-邊界梯度:
使用零法向-邊界梯度:
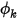 使用零法向-邊界梯度:
使用零法向-邊界梯度: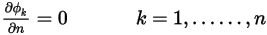
在 Creo Flow Analysis 中,在流動對稱邊界上,對稱也是 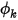 的預設邊界條件。
的預設邊界條件。
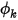 的預設邊界條件。
的預設邊界條件。• 出口
出口是預期流動會進入或離開領域之開口處的邊界條件。對於指定的壓力出口,或流動中的電阻器或電容器,這是純量 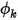 的預設條件。
的預設條件。
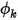 的預設條件。
的預設條件。在出口邊界上,所需的輸入是為純量 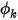 指定的值。適用於
指定的值。適用於 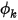 的實際邊界條件取決於流動條件:
的實際邊界條件取決於流動條件:
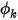 指定的值。適用於
指定的值。適用於 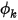 的實際邊界條件取決於流動條件:
的實際邊界條件取決於流動條件:◦ 離開領域的流動 - 當流動從出口的計算領域流出或通過入口反向流動時,假設邊界處為零梯度:

◦ 進入領域的流動 - 當流動從入口的計算領域流入或通過出口反向流動時,將針對邊界使用指定的值:

• 對流通量
在邊界上,規定 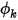 每單位面積的對流通量 (
每單位面積的對流通量 (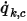 ) 為純量 (
) 為純量 (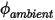 ) 的外部環境值與交換係數 (
) 的外部環境值與交換係數 (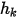 ) 的函數:
) 的函數:
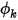 每單位面積的對流通量 (
每單位面積的對流通量 (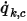 ) 為純量 (
) 為純量 (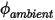 ) 的外部環境值與交換係數 (
) 的外部環境值與交換係數 (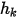 ) 的函數:
) 的函數: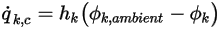
其中,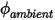 與
與 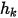 是使用者輸入參數。請注意,交換係數
是使用者輸入參數。請注意,交換係數 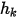 的單位為
的單位為 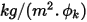 。透過已知對流通量
。透過已知對流通量 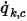 ,可使用方程式 2.376 計算出
,可使用方程式 2.376 計算出 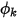 的邊界值。
的邊界值。
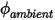 與
與 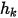 是使用者輸入參數。請注意,交換係數
是使用者輸入參數。請注意,交換係數 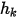 的單位為
的單位為 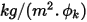 。透過已知對流通量
。透過已知對流通量 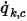 ,可使用方程式 2.376 計算出
,可使用方程式 2.376 計算出 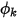 的邊界值。
的邊界值。• 指定的純量通量
在此邊界條件下,可以使用以下兩種方式指定純量的通量:
◦ 單位面積通量 - 在方程式 2.376 中,每單位面積的純量通量 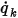 是以常數值或使用者定義的函數形式指定的使用者輸入:
是以常數值或使用者定義的函數形式指定的使用者輸入:
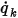 是以常數值或使用者定義的函數形式指定的使用者輸入:
是以常數值或使用者定義的函數形式指定的使用者輸入:
然後,在方程式 2.376 中,可根據流動條件計算出 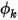 。
。
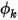 。
。◦ 總通量 - 總純量通量透過以常數值或使用者定義的函數形式指定的使用者輸入計算得出:
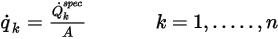
其中 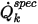 是指定的總純量通量,
是指定的總純量通量,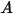 是總邊界面積。然後,可根據流動條件透過方程式 2.376 計算出
是總邊界面積。然後,可根據流動條件透過方程式 2.376 計算出 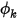 。
。
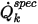 是指定的總純量通量,
是指定的總純量通量,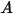 是總邊界面積。然後,可根據流動條件透過方程式 2.376 計算出
是總邊界面積。然後,可根據流動條件透過方程式 2.376 計算出 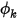 。
。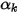 ) 的傳輸進行建模,其中各個相不會混溶 (請參閱
) 的傳輸進行建模,其中各個相不會混溶 (請參閱