物理
本部分通过下列主题对模块中涉及的理论知识及建模过程进行了说明:
标量传输方程
在“物种”(Species) 模块中,Creo Flow Analysis 可求解任意用户定义标量的传输方程。对于任意标量,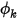 ,一般传输方程的形式如下:
,一般传输方程的形式如下:
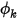 ,一般传输方程的形式如下:
,一般传输方程的形式如下: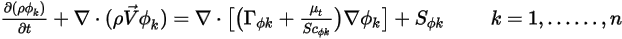
其中 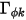 、
、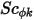 和
和 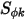 分别为用户指定的扩散系数、湍流施密特数和标量
分别为用户指定的扩散系数、湍流施密特数和标量 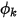 的源项。此处假定
的源项。此处假定 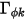 为各向同性。它可以是直接指定的值或用户定义的函数。
为各向同性。它可以是直接指定的值或用户定义的函数。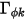 也可通过指定的施密特数间接确定,该值为指定值或用户定义的函数。湍流施密特数
也可通过指定的施密特数间接确定,该值为指定值或用户定义的函数。湍流施密特数 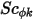 为用户指定的常量,默认值为 1。源项
为用户指定的常量,默认值为 1。源项 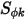 可以是常数或用户定义的函数,其形式为单位体积源或计算域中的总源。
可以是常数或用户定义的函数,其形式为单位体积源或计算域中的总源。
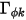 、
、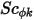 和
和 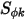 分别为用户指定的扩散系数、湍流施密特数和标量
分别为用户指定的扩散系数、湍流施密特数和标量 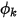 的源项。此处假定
的源项。此处假定 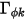 为各向同性。它可以是直接指定的值或用户定义的函数。
为各向同性。它可以是直接指定的值或用户定义的函数。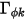 也可通过指定的施密特数间接确定,该值为指定值或用户定义的函数。湍流施密特数
也可通过指定的施密特数间接确定,该值为指定值或用户定义的函数。湍流施密特数 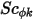 为用户指定的常量,默认值为 1。源项
为用户指定的常量,默认值为 1。源项 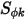 可以是常数或用户定义的函数,其形式为单位体积源或计算域中的总源。
可以是常数或用户定义的函数,其形式为单位体积源或计算域中的总源。请注意,通过选择“物种”模块仅能添加一个标量方程。对于 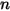 个标量,必须选择该模块
个标量,必须选择该模块 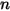 次,并为每个物种分配不同的名称。
次,并为每个物种分配不同的名称。
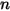 个标量,必须选择该模块
个标量,必须选择该模块 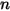 次,并为每个物种分配不同的名称。
次,并为每个物种分配不同的名称。方程 2.376 为一般标量方程。您可针对标量传输单独对其进行求解,也可将其作为任意或所有标准模块的附加方程。由于扩散项和源项由用户输入的常数值或用户定义的函数确定,因此一般标量传输方程可用于开发全新的物理模型,例如湍流和燃烧模型。该方程也可采用仅包含若干项的简化形式。示例如下:
• 泊松和拉普拉斯方程
在稳态模式下,如果对流通量未求解或保持恒定,则方程 2.376 可简化为仅涉及扩散问题:
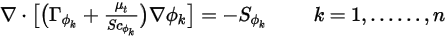
此外,如果忽略湍流扩散 (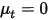 或
或 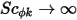 ) 且
) 且 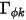 为常数,则方程 2.376 将变为泊松方程:
为常数,则方程 2.376 将变为泊松方程:
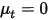 或
或 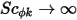 ) 且
) 且 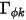 为常数,则方程 2.376 将变为泊松方程:
为常数,则方程 2.376 将变为泊松方程: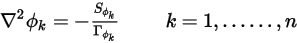
当 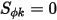 ,可将标量方程 2.376 进一步添加至拉普拉斯方程。
,可将标量方程 2.376 进一步添加至拉普拉斯方程。
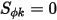 ,可将标量方程 2.376 进一步添加至拉普拉斯方程。
,可将标量方程 2.376 进一步添加至拉普拉斯方程。在许多应用中,如果用体电荷密度 (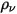 ) 替换
) 替换 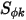 ,且
,且 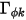 为介电常数 (
为介电常数 (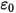 ),则可应用方程 2.376 来计算电场中的电势 (
),则可应用方程 2.376 来计算电场中的电势 (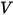 ):
):
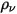 ) 替换
) 替换 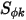 ,且
,且 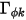 为介电常数 (
为介电常数 (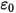 ),则可应用方程 2.376 来计算电场中的电势 (
),则可应用方程 2.376 来计算电场中的电势 (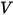 ):
):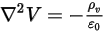
• 对流传输
如果没有扩散项 (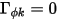 和
和 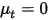 或
或 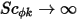 ),则方程 2.376 可简化为:
),则方程 2.376 可简化为:
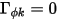 和
和 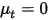 或
或 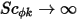 ),则方程 2.376 可简化为:
),则方程 2.376 可简化为: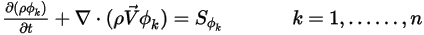
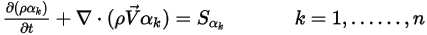
当 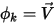 且
且 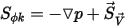 时,方程 2.376 为非粘性流动的欧拉方程:
时,方程 2.376 为非粘性流动的欧拉方程:
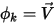 且
且 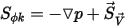 时,方程 2.376 为非粘性流动的欧拉方程:
时,方程 2.376 为非粘性流动的欧拉方程: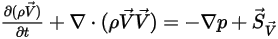
边界条件
用户定义的标量可为任何物理量。因此不会将边界条件定义为流动边界条件。例如,流动入口边界对于标量 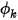 而言可能完全表示不同的含义。因此,对于一般标量传输方程,您可对所选物理边界应用所有已定义的边界类型。
而言可能完全表示不同的含义。因此,对于一般标量传输方程,您可对所选物理边界应用所有已定义的边界类型。
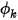 而言可能完全表示不同的含义。因此,对于一般标量传输方程,您可对所选物理边界应用所有已定义的边界类型。
而言可能完全表示不同的含义。因此,对于一般标量传输方程,您可对所选物理边界应用所有已定义的边界类型。如果 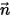 为垂直于局部边界曲面的单位矢量,则单位面积质量通量的一般表达式为:
为垂直于局部边界曲面的单位矢量,则单位面积质量通量的一般表达式为:
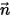 为垂直于局部边界曲面的单位矢量,则单位面积质量通量的一般表达式为:
为垂直于局部边界曲面的单位矢量,则单位面积质量通量的一般表达式为: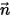
前提是边界处同时存在平流和扩散。
对于标量传输,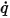 为边界处流出或流入物理域的单位面积通量。根据应用场合的不同,以下公共边界条件派生自此一般方程式:
为边界处流出或流入物理域的单位面积通量。根据应用场合的不同,以下公共边界条件派生自此一般方程式:
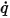 为边界处流出或流入物理域的单位面积通量。根据应用场合的不同,以下公共边界条件派生自此一般方程式:
为边界处流出或流入物理域的单位面积通量。根据应用场合的不同,以下公共边界条件派生自此一般方程式:• 零通量
将跨 (垂直于) 边界的单位面积通量指定为零。如果采用零通量条件 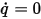 ,则对流和扩散通量必须完全相等:
,则对流和扩散通量必须完全相等:
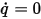 ,则对流和扩散通量必须完全相等:
,则对流和扩散通量必须完全相等: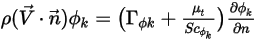
这意味着,如果其中一项为零,则另一项也必须为零。例如,在实体 (壁) 边界处,当曲面的法向速度为零 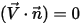 时,
时,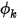 不一定为零。为满足方程 2.376 中的约束,边界处标量的梯度必须为零
不一定为零。为满足方程 2.376 中的约束,边界处标量的梯度必须为零 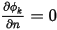 。
。
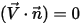 时,
时,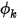 不一定为零。为满足方程 2.376 中的约束,边界处标量的梯度必须为零
不一定为零。为满足方程 2.376 中的约束,边界处标量的梯度必须为零 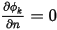 。
。在 Creo Flow Analysis 中的壁面处,零通量为标量 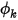 的默认边界条件。
的默认边界条件。
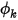 的默认边界条件。
的默认边界条件。• 指定的值
指定的值为通过用户输入值 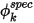 直接确定边界处标量值
直接确定边界处标量值 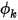 时的边界条件:
时的边界条件:
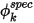 直接确定边界处标量值
直接确定边界处标量值 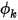 时的边界条件:
时的边界条件:
在 Creo Flow Analysis 中的流动入口处,指定的常数值为 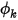 的默认边界条件。
的默认边界条件。
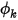 的默认边界条件。
的默认边界条件。• 对称
对于对称边界条件,垂直于边界的零梯度适用于标量 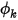 :
:
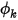 :
: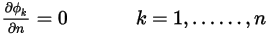
此外,在 Creo Flow Analysis 中的流动对称边界处,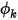 的默认边界条件也是对称。
的默认边界条件也是对称。
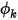 的默认边界条件也是对称。
的默认边界条件也是对称。• 出口
出口可用作开口处的边界条件,流动预计在开口处流出或流入域。对于指定的压力出口或流动中的流阻或流容,此为标量 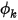 的默认条件。
的默认条件。
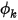 的默认条件。
的默认条件。在出口边界处,所需的输入为标量 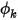 的指定值。适用于
的指定值。适用于 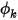 的实际边界条件取决于流动条件:
的实际边界条件取决于流动条件:
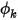 的指定值。适用于
的指定值。适用于 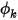 的实际边界条件取决于流动条件:
的实际边界条件取决于流动条件:◦ 流出域的流动 - 当流动从出口或通过反向流在入口处流出计算域时,假定边界处的梯度为零:

◦ 流入域的流动 - 当流动从入口或通过反向流在出口处流入计算域时,所指定的值适用于边界:

• 对流通量
在边界处,单位面积 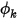 的对流通量 (
的对流通量 (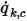 ) 经确定为标量的外部环境值 (
) 经确定为标量的外部环境值 (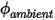 ) 与交换系数 (
) 与交换系数 (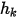 ) 的函数:
) 的函数:
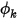 的对流通量 (
的对流通量 (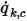 ) 经确定为标量的外部环境值 (
) 经确定为标量的外部环境值 (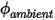 ) 与交换系数 (
) 与交换系数 (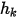 ) 的函数:
) 的函数: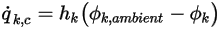
其中 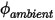 和
和 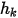 为用户输入参数。请注意,交换系数
为用户输入参数。请注意,交换系数 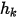 的单位为
的单位为 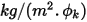 。基于已知的对流通量
。基于已知的对流通量 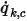 ,
,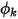 的边界值可通过方程 2.376 求得。
的边界值可通过方程 2.376 求得。
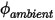 和
和 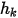 为用户输入参数。请注意,交换系数
为用户输入参数。请注意,交换系数 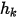 的单位为
的单位为 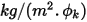 。基于已知的对流通量
。基于已知的对流通量 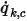 ,
,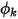 的边界值可通过方程 2.376 求得。
的边界值可通过方程 2.376 求得。• 指定的标量通量
在此边界条件下,可通过以下两种方式指定标量的通量:
◦ 单位面积通量 - 在方程 2.376 中,单位面积标量通量 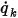 由用户输入指定为常数值或用户定义的函数:
由用户输入指定为常数值或用户定义的函数:
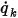 由用户输入指定为常数值或用户定义的函数:
由用户输入指定为常数值或用户定义的函数:
然后,通过方程 2.376,基于流动条件求得 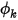 。
。
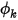 。
。◦ 总通量 - 总标量通量由用户输入的常数值或用户定义的函数确定:
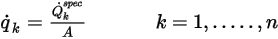
其中 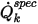 为指定的总标量通量,
为指定的总标量通量,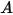 为总边界面积。然后,可基于流动条件通过方程 2.376 求得
为总边界面积。然后,可基于流动条件通过方程 2.376 求得 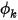 。
。
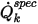 为指定的总标量通量,
为指定的总标量通量,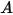 为总边界面积。然后,可基于流动条件通过方程 2.376 求得
为总边界面积。然后,可基于流动条件通过方程 2.376 求得 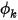 。
。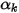 ) 的传输进行建模,其中各个相互不相溶 (请参阅
) 的传输进行建模,其中各个相互不相溶 (请参阅