Include Snap-Through
The snap-through behavior is an instability in the displacements of a structure. The displacement jumps from one configuration to another, even without an increase of the external load.
Snap back behavior is an instability in the displacements of a structure, where the displacement jumps from one configuration to another, even without an increase in the prescribed displacement.
For most nonlinear analyses, the Newton-type method (Load Control Method) is used to converge to the solution at each step along the force-deflection curve. The load is increased by a finite amount at each sub-step and the load is kept fixed throughout the equilibrium iterations. In the case of snap-through (under load control) two solutions may exist at a limit point. Under an increasing load, the displacements may then make a jump and the analysis is unlikely to converge due to the magnitude of the jump. For the displacement control method too, convergence may not occur when there is a large jump in the load.
The following figure shows the load displacement curve for a non linear analysis where λ is applied load and μ is displacement.
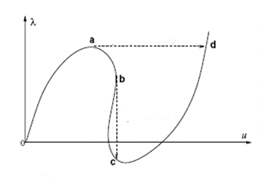
1. o-a-d : snap-through (under load control)
2. o-a-b-c : snap-under (under displacement control)
In this example, under the Load Control Method, the analysis fails to converge after point a or traces the path o-a-d, providing incomplete or misleading information about the stability of the structure. For the displacement control method too, the analysis may fail to converge after point b and describe the path o-a-b-c.
In the Load Control Method, the load step is kept constant and in the Displacement Control Method the displacement step is kept constant. However, in the Arc-Length Method algorithm, the load-factor is modified by a factor at each iteration so that the solution follows a specified path until convergence is achieved. This method records the additional load and displacement pairs of the equilibrium path.
About Arc Length Methods in Nonlinear Analyses
The complete investigation of solution paths of the nonlinear system of equilibrium equations has a strong practical interest in the study of the overall critical behavior of structures. Methods that use general path-following are called arc-length methods. The essential idea of such methods is to add a constraint condition to the set of nonlinear equations from which the unknown load parameter can be determined. Since path-following methods are well established, literature is available on a number of different methods. Among the many existing incremental iterative nonlinear solution methods, the arc-length method developed by Riks (1979) and later modified by Crisfield (1981) are the most popular. Creo Simulate uses the Crisfield arc length method.
For simple structures, all that one may need is to find the load level at the limit point where the structure will not take any further load and will collapse. Collapse loads are often associated with a failure to achieve convergence with the iterative solution procedure. For other models, it may be important to perform analysis of individual components of the structure and obtain the information on the nature of the response, post limit points (see Fig 1). This allows you to access the performance and stability of the complete structure and gain an insight into the behavior of the structure while passing through unstable regions as seen in Fig 2.
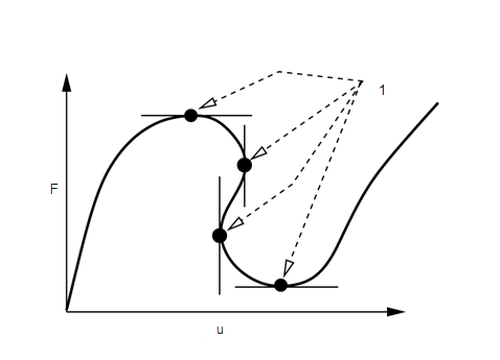
Fig 1
1. limit points
2. F—load
3. u—displacement
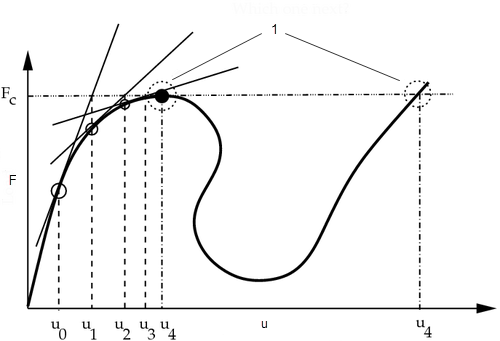
Fig 2
1. which point next?
2. F—load
3. u—displacement
Crisfield’s Spherical Arc-length method
Crisfield (1981) used the hypersphere in his arc-length method. This approach in combination with the modified Newton-Raphson (m.N-R) method is used as an iterative procedure. In this method, the tangent stiffness matrix is neither re-formed nor re-factored at each iteration but instead held fixed and is only formed and factored at the beginning of each load increment. Fig 4 qualitatively illustrates Crisfield’s method with m.N-R for a one dimensional problem.
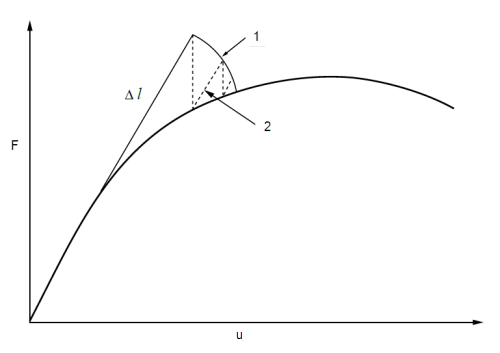
Fig 4
1. hypersphere
2. equilibrium iterations
3. F—external force
4. u—displacement
When you select Include Snap-through on the Convergence tab, Crisfield’s spherical arc length method is activated, that ensures accurate tracing of the load-displacement curve in snap-through and snap-back structures.
For a large deformation analysis if you select Single-Pass Adaptive or Quick Check for the convergence method, select Include Snap-through to activate the arc length algorithm. Load displacement history is now available for snap-through and post-buckling problems. You must select this option only when required as this option involves an additional computational cost.
For a snap-through or post buckling analysis Creo Simulate records the start and end of snap-through in the Summary .rpt file.
To further investigate the output you can also use the following configuration options:
• sim_newton_debugprint—Set the value of this option to yes to print detailed debugging information to the .pas file for both the mN-R as well as the arc length method.
• sim_nl_ldc—Prints the load deflection curve to the .ldc file when set to yes. The .ldc file is a text file with comma separated values for load and displacement for each output time step.
• sim_snap_tolerance_factor—Determines whether to start or delay snap-through. Set this option to a value greater than 1 to delay snap-through. To start snap-through earlier, set the value of this option to a value less than 1.
You can view the load displacement curve for a snap-through or buckling analysis by viewing a displacement measure versus applied load graph as described in To View Snap Through in Results.
Return to Convergence Options for Structural Analyses or To Create a Static Analysis with Large Deformation.
Guidelines for Selecting the Best Method for Analysis
• As anticipated in literature, the performance of arc-length methods is least satisfactory when the structure oscillates over a short length of the load-deflection path, between stable and unstable equilibrium. You start noticing a structure collapse error when arc-length methods converge to limit points. Theoretically the structure stiffness at such points is either zero or infinite which leads to numerical failures. In general, in scenarios when your solution converges to limit points, it is worth trying different output steps to make sure you are not accidently placing steps near limit points. Arrange your output steps to avoid such limit points if possible, or take make the output steps larger to avoid limit points. For short length snapping phenomenon the default m.N-R method proves to be more robust than the arc-length methods. A simulation with the default m.N-R method and with reasonably fine steps will give you more insight into such cases.
• Using the Crisfield arc length with m.N-R method helps to solve problems involving both horizontal and vertical tangent limit points. Numerical experiences with the arc-length methods are very encouraging when the structure oscillates over a long length of the load-deflection path between stable and unstable equilibrium. The speed of convergence and the steps chosen by the algorithms are very efficient in such models.
The choice of method needs some engineering judgement. If both methods fail to converge, you may want to review your model, loads or solution strategy.
Bibliography
1. E. Ricks, An incremental approach to the solution of snapping and buckling problems. Int. J. Solids Structures 15,524-551 (1979).
2. Crisfield M.A. A fast incremental/iterative solution procedure that handles snap-through. Computer and Structures, 13(1):55–62, 1981