Wall Physics
Log Law of the Wall:
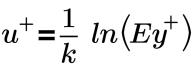
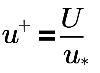
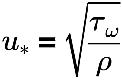
where,
u+ | dimensionless velocity |
U | local (cell center) velocity |
u* | friction velocity |
τω | wall shear |
ρ | fluid velocity |
E | constant coefficient |
k | Von Karman Constant (0.41) |
y+ | nondimensional wall-to-cell distance |
Wall Functions and Laws
Wall function is necessary to model near-wall behavior of turbulent boundary layers in the absence of extremely dense grid distributions at a no-slip boundary (wall). A large variety of wall function exists in literature and it is advisable to research what is appropriate for a particular application. The usage of wall function is a subject of Boundary Layer Theory Schlichting (Boundary Layer Theory, 6th Edition, 1968 ISBN 07-055329-7).
The nondimensional distance y+ from the wall to a point in the adjacent flow is defined as:
where,
friction velocity | |
v | kinematic viscosity |
• viscous sublayer 0 < y+< 5
• buffer layer 5 < y+< 30
• inertial layer 30 < y+< 200
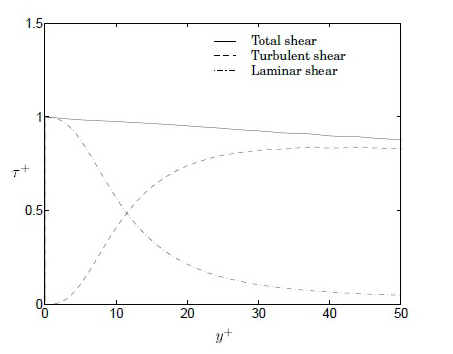
There are several wall functions developed to support the turbulent viscosity models explained here:
• Standard—Proposed by Launder and Spalding and defines the turbulent mean velocity profile near the wall. The law-of-the-wall for mean velocity distribution using the Standard wall function is formulated as follows:
In the inertial sublayer and the viscous sublayer:
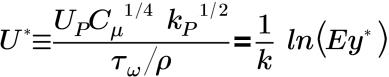
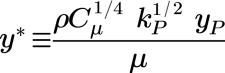
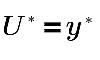
where,
k=0.4187 | Von Karman constant |
E=9.793 | empirical constant |
UP | mean velocity of the fluid at point P |
kP | turbulence kinetic energy at point P |
yP | distance from point P to the wall |
μ | dynamic viscosity of the fluid |
The Standard wall function is used in industrial applications and is also described in documents about fluid flow. It was derived under the assumption of local equilibrium of turbulence kinetic energy production K and turbulence energy rate of dissipation. The Standard wall function is most accurate when predicting flows with small pressure gradients, no separation, no recirculation, and negligible acceleration or deceleration effects.
• Nonequilibrium(Kim)—Proposed by Kim, defines the turbulent mean velocity profile near the wall. The law of the wall for mean velocity distribution using the Nonequilibrium(Kim) wall function is formulated as follows:
In the inertial sublayer:
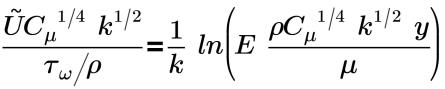
k=0.4187 | Von Karman constant |
E=9.793 | empirical constant |
UP | mean velocity of the fluid at point P |
kP | turbulence kinetic energy mean velocity of the fluid at point P |
yP | distance from point P to the wall turbulence kinetic energy mean velocity of the fluid at point P |
μ | dynamic viscosity of the fluid turbulence kinetic energy mean velocity of the fluid at point P |
Cμ | 0.09 |
The Nonequilibrium(Kim) wall function assumes that the turbulence kinetic energy production does not equal the rate of dissipation. The Nonequilibrium(Kim) wall function considers the pressure gradient effects. It uses a two-layer model for treatment of the viscous sublayer and fully turbulent inertial layer. The Nonequilibrium(Kim) wall function uses an enhanced wall treatment which uses blending functions in the wall buffer region (3 < y+ < 10) for a smooth transition between the linear law in the viscous sublayer and the logarithmic law in the inertial sublayer.
• Unified(Shih)—Proposed by Shih, defines the turbulent mean velocity profile across the boundary layer. The law of the wall for mean velocity distribution using the Unified(Shih) wall function is formulated as follows:
Across entire boundary layer where f1(Yτ+) and f2(Yρ+) are piecemeal fitting functions:
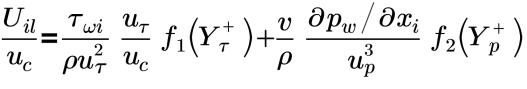
The Unified (Shih) wall function is valid in the viscous sublayer, buffer layer, and inertial sublayer (unified). The Unified (Shih) wall function behaves well for flows with both favorable and adverse pressure gradients, wall-bounded complex flows with acceleration, deceleration, and recirculation. This wall function uses a three-layer model for treatment of the viscous sublayer, buffer layer, and inertial sublayer.
Wall Roughness Model
Wall Roughness Model refers to the roughness in meter of the surface finish on a wall.
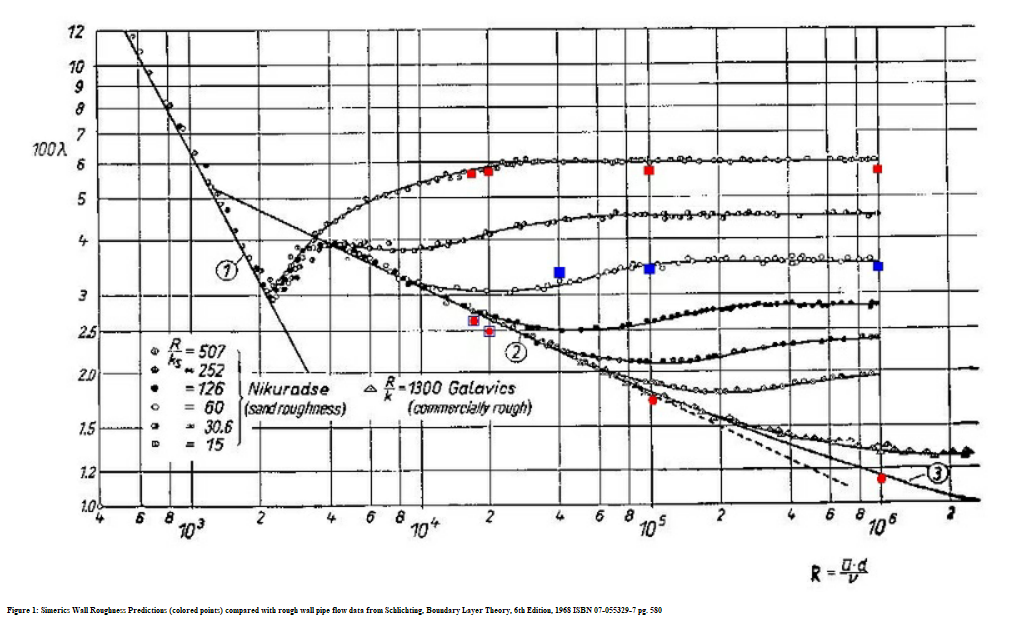
Creo Flow Analysis wall roughness predictions (colored points) compared with rough wall pipe flow data Schlichting, Boundary Layer Theory, 6th Edition, 1968 ISBN 07-055329-7 pg. 580.