Example: Cylindrical Spline Surface Data Format
The cylindrical spline surface is a nonuniform bicubic spline surface that passes through a grid with tangent vectors given at each point. The grid is curvilinear in uv space.
The following illustration shows a cylindrical spline surface.
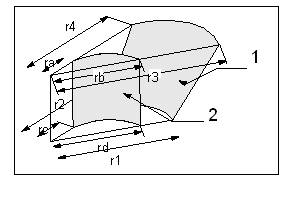
1. Cone surface S1
2. Cylindrical surface, S0 Spline
Data format:
e1[3] | x' vector of the local coordinate system |
e2[3] | y' vector of the local coordinate system |
e3[3] | z' vector of the local coordinate system, which corresponds to the axis of revolution of the surface |
origin[3] | Origin of the local coordinate system |
splsrf | Spline surface data structure |
The spline surface data structure contains the following fields:
u_par_arr[] | Point parameters, in the u direction, of size Nu |
v_par_arr[] | Point parameters, in the v direction, of size Nv |
point_arr[][3] | Array of points, in cylindrical coordinates, of size, Nu & Nv. The array components are as follows: point_arr[i][0]—Radius point_arr[i][1]—Theta point_arr[i][2]—Z |
u_tan_arr[][3] | Array of u tangent vectors in cylindrical coordinates, of size Nu & Nv |
v_tan_arr[][3] | Array of v tangent vectors in cylindrical coordinates, of size Nu & Nv |
uvder_arr[][3] | Array of mixed derivatives in cylindrical coordinates, of size Nu & Nv |
Engineering Notes
If the surface is represented in cylindrical coordinates (r, theta, z), the local coordinate system values (x', y', z') are interpreted as follows:
• x' = r cos (theta)
• y' = r sin (theta)
• z' = z
You can obtain a cylindrical spline surface, for example, by creating a smooth rotational blend (shown in the figure on the previous page). In some cases, you can replace a cylindrical spline surface with a surface such as a plane, cylinder, or cone. The illustration shows the cylindrical spline surface S1 replaced with a cone (r1=r2, r3=r4, and r1r3). If you cannot replace it (such as for the surface S0 in the illustration Cylindrical Spline Surface (ra≠rb or rc≠rd), leave it as a cylindrical spline surface representation.