Варианты проверок - статические структурные анализы
Прямоугольная плита с круглым отверстием, подвергающаяся растягивающему нагружению
Постановка задачи: прямоугольная плита с круглым отверстием зафиксирована вдоль одной из граней, и растягивающая нагрузка давлением приложена к противоположной грани. Ищем максимальное нормальное напряжение в направлении X на цилиндрических поверхностях отверстия.
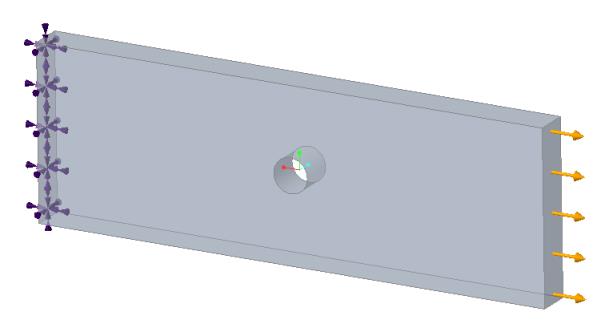
Привязки:
J. E. Shigley, Mechanical Engineering Design, McGraw-Hill, 1st Edition, 1986, Таблица A-23, Рис A-23-1, стр. 673
Свойства материала | Геометрические свойства | Нагружение |
|---|---|---|
Модуль Юнга, E = 1000 Па Коэффициент Пуассона, ν = 0.0 | Длина = 15 м Ширина = 5 м Толщина = 1 м Радиус отверстия = 0.5 м | Давление = -100 Па |
Сравнение результатов - ползунок качества моделирования в позиции по умолчанию
Результаты | Цель | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Ошибка в процентах |
|---|---|---|---|---|---|
Максимальное напряжение по нормали к оси X (Па) | 312.5 | 313.272 | 270.69 | 265.11 | 15.16 |
Сравнение результатов - ползунок качества моделирования в максимальной позиции
Результаты | Цель | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Ошибка в процентах |
|---|---|---|---|---|---|
Максимальное напряжение по нормали к оси X (Па) | 312.5 | 313.272 | 302.36 | 290.60 | 7.53 |
Сравнение результатов для Creo Ansys Simulation
(Разрешение сетки по умолчанию с размером грани = 0.15 м на поверхности отверстия с использованием метода функции кривизны и размера близости.)
Результаты | Цель | Ansys AIM | Creo Ansys Simulation | Ошибка в процентах |
|---|---|---|---|---|
Максимальное напряжение по нормали к оси X (Па) | 312.5 | 310.7 | 310.397 | 0.67 |
Ступенчатый вал при осевом растяжении
Постановка задачи: рассмотрим ступенчатый вал с приложенной осевой нагрузкой 1000 фунт-сила/кв. дюйм к наименьшему сечению вала, рассчитаем концентрацию напряжений на основе радиуса закругления на ступени, как показано ниже:
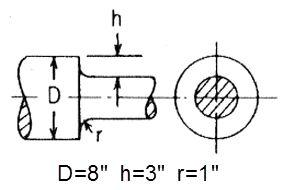
Ссылка:Roark’s Formulas for Stress and Strain, Warren C. Young and Richard G. Budynas, 2002
Свойства материала | Геометрические свойства | Нагружение |
|---|---|---|
Модуль Юнга, E = 2.9008e7 фунт на кв. дюйм Коэффициент Пуассона, ν = 0.3 | D = 8 дюймов h = 3 дюйма r = 1 дюйм | Давление = -1000 фунт-сила/кв. дюйм |
Сравнение результатов - ползунок качества моделирования в позиции по умолчанию
Результаты | Цель | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Ошибка в процентах |
|---|---|---|---|---|---|
Максимальное напряжение по нормали к оси Y (фунт-сила/кв. дюйм) | 1376 | 1422.63 | 1526.5 | 1488 | 7.53 |
Сравнение результатов для Ansys AIM и Creo Ansys Simulation (максимальное разрешение сетки)
Результаты | Цель | Ansys AIM | Creo Ansys Simulation | Ошибка в процентах |
|---|---|---|---|---|
Максимальное напряжение по нормали к оси Y (фунт-сила/кв. дюйм) | 1376 | 1410.96 | 1466.68 | 6.18 |
Удлинение сплошного стержня
Постановка задачи: клиновидный стержень из алюминиевого сплава квадратного поперечного сечения с длиной L свисает с потолка. Осевая нагрузка F приложена к свободному концу стержня. Определим максимальное осевое отклонение d в стержне и осевое напряжение σy в середине длины (Y = L/2).
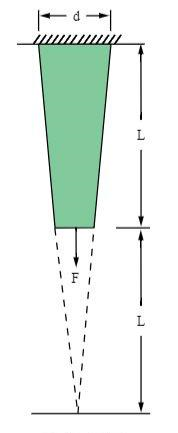
Ссылка: C. O. Harris, Introduction to Stress Analysis, The Macmillan Co., New York, NY, 1959,стр. 237, задача 4
Свойства материала | Геометрические свойства | Нагружение |
|---|---|---|
Модуль Юнга, E = 10.4e6 фунт на кв. дюйм Коэффициент Пуассона, ν = 0.3 | L = 10 дюймов d = 2 дюйма | F = 10000 фунт-сила |
Сравнение результатов - ползунок качества моделирования в позиции по умолчанию.
Результаты | Цель | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Ошибка в процентах |
|---|---|---|---|---|---|
Деформация в направлении Y (дюймы) | 0.0048077 | 0.0048156 | 0.0048 | 0.0048 | 0,15 |
Напряжение по нормали к оси Y на L/2 (фунт-сила/кв. дюйм) | 4444 | 4439.45 | 4446.2 | 4415.46 | 0.65 |
Сравнение результатов для Ansys AIM и Creo Ansys Simulation (сетка по умолчанию)
Результаты | Цель | Ansys AIM | Creo Ansys Simulation | Ошибка в процентах |
|---|---|---|---|---|
Деформация в направлении Y (дюймы) | 0.0048077 | 0.0048266 | 0.0048266 | 0.39 |
Напряжение по нормали к оси Y на L/2 (фунт-сила/кв. дюйм) | 4444 | 4443.1 | 4582 | 3.01 |
Круглая плита под равномерным давлением
Постановка задачи: рассмотрим круглую плиту с фиксированными кромками под однородно распределенной нагрузкой давлением. Ищем максимальное отклонение в центре плиты.
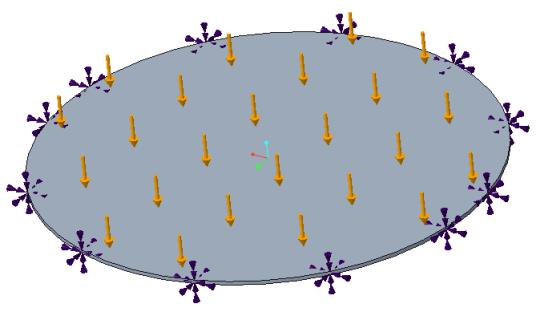
Ссылка: R. J. Roark, W. C. Young,Formulas for Stress and Strain, McGraw-Hill Book Co., Inc.,New York, NY, 1975, Таблица 24.
Свойства материала | Геометрические свойства | Нагружение |
|---|---|---|
Модуль Юнга, E = 30e6 фунт на кв. дюйм Коэффициент Пуассона, ν = 0.3 | Диаметр = 30 дюймов Толщина = 0.25 дюйма | P = 3 фунт-сила/кв. дюйм |
Результаты - ползунок качества моделирования в позиции по умолчанию
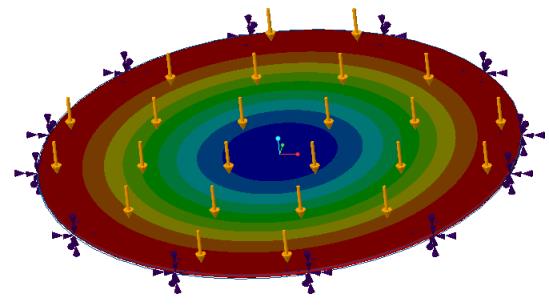
Сравнение результатов - ползунок качества моделирования в положении максимума для графической карты M2000
Результаты | Цель | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Ошибка в процентах |
|---|---|---|---|---|---|
Отклонение центра плиты, дюймы. | 0.0553 | 0.0549 | 0.0546 | 0.0545 | 1.47 |
Сравнение результатов - ползунок качества моделирования в положении максимума для графической карты P4000
Результаты | Цель | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Ошибка в процентах |
|---|---|---|---|---|---|
Отклонение центра плиты (дюйм) | 0.0553 | 0.0549 | 0.0590 | 0.0527 | 4.93 |
Сравнение результатов для Creo Ansys Simulation (максимальное разрешение сетки)
Результаты | Цель | Ansys AIM | Creo Ansys Simulation | Ошибка в процентах |
|---|---|---|---|---|
Отклонение центра плиты (дюйм) | 0.0553 | 0.05505 | 0.05505 | 0,45 |