Физика
В следующих разделах этой главы описывается теория и моделирование в модуле:
Скалярное уравнение переноса
В модуле Вещества (Species)Creo Flow Analysis решает уравнение переноса для произвольного определяемого пользователем скаляра. Для произвольного скаляра 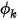 общее уравнение переноса имеет вид:
общее уравнение переноса имеет вид:
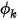 общее уравнение переноса имеет вид:
общее уравнение переноса имеет вид: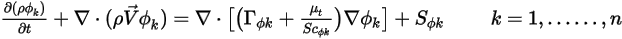
где 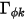 ,
, 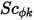 и
и 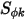 - определяемый пользователем коэффициент диффузии, турбулентное число Шмидта и член источника для скаляра
- определяемый пользователем коэффициент диффузии, турбулентное число Шмидта и член источника для скаляра 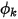 соответственно. Здесь
соответственно. Здесь 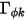 предполагается изотропным. Это может быть непосредственно заданное значение или определяемая пользователем функция.
предполагается изотропным. Это может быть непосредственно заданное значение или определяемая пользователем функция. 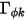 также неявно определяется через указанное число Шмидта, которое является указанным значением или определяемой пользователем функцией. Турбулентное число Шмидта
также неявно определяется через указанное число Шмидта, которое является указанным значением или определяемой пользователем функцией. Турбулентное число Шмидта 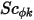 является определяемой пользователем константой со значением по умолчанию, равным единице. Член источника
является определяемой пользователем константой со значением по умолчанию, равным единице. Член источника 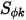 может быть задан как постоянная или определяемая пользователем функция в виде источника на объем или общего источника в расчетной области.
может быть задан как постоянная или определяемая пользователем функция в виде источника на объем или общего источника в расчетной области.
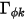 ,
, 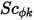 и
и 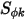 - определяемый пользователем коэффициент диффузии, турбулентное число Шмидта и член источника для скаляра
- определяемый пользователем коэффициент диффузии, турбулентное число Шмидта и член источника для скаляра 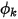 соответственно. Здесь
соответственно. Здесь 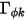 предполагается изотропным. Это может быть непосредственно заданное значение или определяемая пользователем функция.
предполагается изотропным. Это может быть непосредственно заданное значение или определяемая пользователем функция. 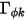 также неявно определяется через указанное число Шмидта, которое является указанным значением или определяемой пользователем функцией. Турбулентное число Шмидта
также неявно определяется через указанное число Шмидта, которое является указанным значением или определяемой пользователем функцией. Турбулентное число Шмидта 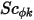 является определяемой пользователем константой со значением по умолчанию, равным единице. Член источника
является определяемой пользователем константой со значением по умолчанию, равным единице. Член источника 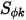 может быть задан как постоянная или определяемая пользователем функция в виде источника на объем или общего источника в расчетной области.
может быть задан как постоянная или определяемая пользователем функция в виде источника на объем или общего источника в расчетной области.Обратите внимание, что при выборе модуля "Вещества" (Species) добавляется только одно скалярное уравнение. Для скаляров 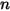 модуль должен выбираться
модуль должен выбираться 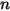 раз, а каждому веществу должно назначаться уникальное наименование.
раз, а каждому веществу должно назначаться уникальное наименование.
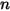 модуль должен выбираться
модуль должен выбираться 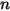 раз, а каждому веществу должно назначаться уникальное наименование.
раз, а каждому веществу должно назначаться уникальное наименование.Уравнение 2.376 является общим скалярным уравнением. Оно может решаться отдельно для скалярного переноса или как дополнение к любому или ко всем стандартным модулям. Поскольку члены диффузии и источника определяются пользовательскими входными данными как константы или пользовательские функции, общее скалярное уравнение можно использовать для разработки новых физических моделей, таких как модели турбулентности и горения. Оно также может использоваться в сокращенном виде, в котором содержатся только некоторые из членов в уравнении. Примеры приводятся ниже:
• Уравнение Пуассона и Лапласа
В режиме стационарного состояния, если конвективный поток не решается или остается неизменным, уравнение 2.376 сводится только к проблеме диффузии.
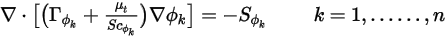
Кроме того, если турбулентная диффузия игнорируется (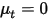 или
или 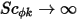 ), а
), а 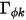 является константой, уравнение 2.376 становится уравнением Пуассона:
является константой, уравнение 2.376 становится уравнением Пуассона:
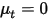 или
или 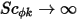 ), а
), а 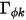 является константой, уравнение 2.376 становится уравнением Пуассона:
является константой, уравнение 2.376 становится уравнением Пуассона: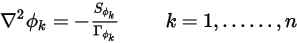
И когда 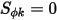 , скалярное уравнение 2.376 добавляется в уравнение Лапласа.
, скалярное уравнение 2.376 добавляется в уравнение Лапласа.
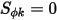 , скалярное уравнение 2.376 добавляется в уравнение Лапласа.
, скалярное уравнение 2.376 добавляется в уравнение Лапласа.Для многих приложений, если 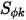 заменяется на объемную плотность заряда (
заменяется на объемную плотность заряда (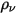 ), а
), а 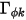 представляет диэлектрическую проницаемость (
представляет диэлектрическую проницаемость (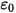 ), то уравнение 2.376 можно применить для расчета электрического потенциала (
), то уравнение 2.376 можно применить для расчета электрического потенциала (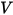 ) в электрическом поле:
) в электрическом поле:
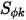 заменяется на объемную плотность заряда (
заменяется на объемную плотность заряда (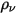 ), а
), а 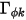 представляет диэлектрическую проницаемость (
представляет диэлектрическую проницаемость (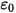 ), то уравнение 2.376 можно применить для расчета электрического потенциала (
), то уравнение 2.376 можно применить для расчета электрического потенциала (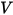 ) в электрическом поле:
) в электрическом поле: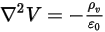
• Конвективный перенос
Без члена диффузии (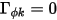 и
и 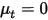 или
или 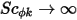 ) уравнение 2.376 сводится к следующему:
) уравнение 2.376 сводится к следующему:
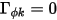 и
и 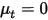 или
или 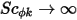 ) уравнение 2.376 сводится к следующему:
) уравнение 2.376 сводится к следующему: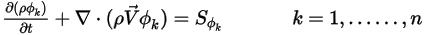
Уравнение 2.376 можно использовать для моделирования переноса объемных долей фаз (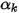 ) в многофазных потоках, в которых эти фазы не смешиваются (см. модуль Многофазный (Multiphase)):
) в многофазных потоках, в которых эти фазы не смешиваются (см. модуль Многофазный (Multiphase)):
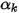 ) в многофазных потоках, в которых эти фазы не смешиваются (см. модуль Многофазный (Multiphase)):
) в многофазных потоках, в которых эти фазы не смешиваются (см. модуль Многофазный (Multiphase)):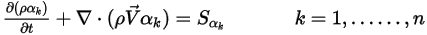
Если 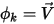 и
и 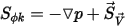 , уравнение 2.376 представляет уравнения Эйлера для невязких потоков:
, уравнение 2.376 представляет уравнения Эйлера для невязких потоков:
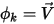 и
и 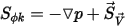 , уравнение 2.376 представляет уравнения Эйлера для невязких потоков:
, уравнение 2.376 представляет уравнения Эйлера для невязких потоков: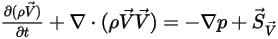
Граничные условия
Определяемый пользователем скаляр может представлять любую физическую величину. Граничные условия, таким образом, не определяются как граничные условия потока. Например, входная граница потока может означать что-то совершенно другое для скаляра 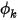 . В результате для общего скалярного уравнения можно применять все определенные типы границ для выбранных физических границ.
. В результате для общего скалярного уравнения можно применять все определенные типы границ для выбранных физических границ.
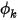 . В результате для общего скалярного уравнения можно применять все определенные типы границ для выбранных физических границ.
. В результате для общего скалярного уравнения можно применять все определенные типы границ для выбранных физических границ.Если 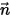 является единичным вектором, нормальным к локальной граничной поверхности, то общее выражение для массового потока через единицу площади имеет вид:
является единичным вектором, нормальным к локальной граничной поверхности, то общее выражение для массового потока через единицу площади имеет вид:
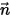 является единичным вектором, нормальным к локальной граничной поверхности, то общее выражение для массового потока через единицу площади имеет вид:
является единичным вектором, нормальным к локальной граничной поверхности, то общее выражение для массового потока через единицу площади имеет вид: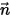
если на границе одновременно имеют место адвекция и диффузия.
Для скалярного переноса 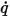 представляет поток через единицу площади, которая выходит из физической области или входит в нее через границу. В зависимости от приложений следующие общие граничные условия выводятся из этой общей формулы.
представляет поток через единицу площади, которая выходит из физической области или входит в нее через границу. В зависимости от приложений следующие общие граничные условия выводятся из этой общей формулы.
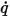 представляет поток через единицу площади, которая выходит из физической области или входит в нее через границу. В зависимости от приложений следующие общие граничные условия выводятся из этой общей формулы.
представляет поток через единицу площади, которая выходит из физической области или входит в нее через границу. В зависимости от приложений следующие общие граничные условия выводятся из этой общей формулы.• Нулевой поток
Поток через единицу площади через границу (по нормали) задается как нулевой. С условием нулевого потока, 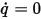 , конвективный и диффузионный потоки должны точно балансироваться:
, конвективный и диффузионный потоки должны точно балансироваться:
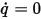 , конвективный и диффузионный потоки должны точно балансироваться:
, конвективный и диффузионный потоки должны точно балансироваться: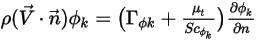
Это означает, что если один член равен нулю, то другой также должен быть нулевым. Например, на твердой поверхности (стенка) скорость по нормали к поверхности равна нулю, 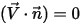 , но значение
, но значение 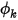 может быть ненулевым. Чтобы удовлетворить ограничению в уравнении 2.376, градиент скаляра на границе должен равняться нулю,
может быть ненулевым. Чтобы удовлетворить ограничению в уравнении 2.376, градиент скаляра на границе должен равняться нулю, 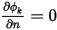 .
.
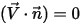 , но значение
, но значение 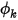 может быть ненулевым. Чтобы удовлетворить ограничению в уравнении 2.376, градиент скаляра на границе должен равняться нулю,
может быть ненулевым. Чтобы удовлетворить ограничению в уравнении 2.376, градиент скаляра на границе должен равняться нулю, 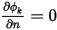 .
.В Creo Flow Analysis нулевой поток на стенке является граничным условием по умолчанию для скаляра 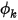 .
.
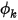 .
.• Указанное значение
Указанное значение является граничным условием, в котором значение скаляра на границе 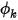 определяется непосредственно пользовательским входным значением
определяется непосредственно пользовательским входным значением 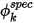 :
:
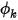 определяется непосредственно пользовательским входным значением
определяется непосредственно пользовательским входным значением 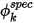 :
:
В Creo Flow Analysis на входном отверстии потока указанное постоянное значение является граничным условием по умолчанию для 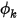 .
.
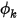 .
.• Симметрия
Для граничного условия симметрии для скаляра применяется нулевой градиент по нормали к границе  :
:
 :
: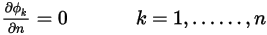
В Creo Flow Analysis на границе с симметрией потока симметрия также является граничным условием по умолчанию для 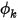 .
.
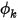 .
.• Выход
Выход (Outlet) используется как граничные условия в отверстии, через которое ожидается выход потока из области или его вход в область. Для заданного давления на выходе или при наличии сопротивления или емкости в потоке это условие применяется по умолчанию для скаляра 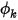 .
.
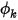 .
.На границе выходного отверстия требуется ввод указанного значения для скаляра 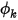 . Фактическое граничное условие, примененное для
. Фактическое граничное условие, примененное для 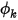 , зависит от условий потока:
, зависит от условий потока:
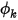 . Фактическое граничное условие, примененное для
. Фактическое граничное условие, примененное для 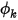 , зависит от условий потока:
, зависит от условий потока:◦ Поток, выходящий из области - если поток выходит из расчетной области через выходное отверстие или через входное отверстие (в случае обратного потока), на границе предполагается нулевой градиент:

◦ Поток, входящий в область - если поток входит в расчетную область через входное отверстие или через выходное отверстие (в случае обратного потока), для границы применяется указанное значение.

• Конвективный поток
На границе конвективный поток 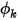 на единицу площади (
на единицу площади (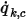 ) определяется как функция внешнего значения скаляра (
) определяется как функция внешнего значения скаляра (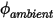 ) и коэффициента обмена (
) и коэффициента обмена (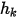 ):
):
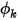 на единицу площади (
на единицу площади (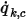 ) определяется как функция внешнего значения скаляра (
) определяется как функция внешнего значения скаляра (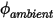 ) и коэффициента обмена (
) и коэффициента обмена (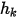 ):
):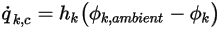
Здесь 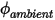 и
и 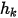 - пользовательские входные параметры. Имейте в виду, что коэффициент обмена
- пользовательские входные параметры. Имейте в виду, что коэффициент обмена 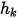 имеет единицу измерения
имеет единицу измерения 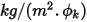 . В случае известного конвективного потока
. В случае известного конвективного потока 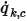 граничное значение
граничное значение 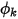 получается из уравнения 2.376
получается из уравнения 2.376
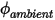 и
и 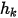 - пользовательские входные параметры. Имейте в виду, что коэффициент обмена
- пользовательские входные параметры. Имейте в виду, что коэффициент обмена 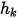 имеет единицу измерения
имеет единицу измерения 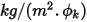 . В случае известного конвективного потока
. В случае известного конвективного потока 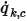 граничное значение
граничное значение 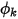 получается из уравнения 2.376
получается из уравнения 2.376• Указанный скалярный поток
В этом граничном условии скалярный поток задается двумя способами:
◦ Поток на единицу площади - в уравнении 2.376 скалярный поток на единицу площади 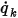 определяется пользовательскими входными данными как константа или определяемая пользователем функция:
определяется пользовательскими входными данными как константа или определяемая пользователем функция:
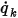 определяется пользовательскими входными данными как константа или определяемая пользователем функция:
определяется пользовательскими входными данными как константа или определяемая пользователем функция:
Тогда из уравнения 2.376 получаем 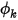 на основе условий потока.
на основе условий потока.
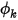 на основе условий потока.
на основе условий потока.◦ Полный тепловой поток - полный скалярный поток известен через пользовательские входные данные как постоянное значение или определяемую пользователем функцию.
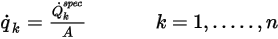
Здесь 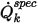 - заданный полный скалярный поток,
- заданный полный скалярный поток, 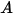 - общая площадь границы. Тогда получаем
- общая площадь границы. Тогда получаем 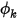 из уравнения 2.376 на основе условий потока.
из уравнения 2.376 на основе условий потока.
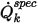 - заданный полный скалярный поток,
- заданный полный скалярный поток, 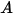 - общая площадь границы. Тогда получаем
- общая площадь границы. Тогда получаем 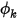 из уравнения 2.376 на основе условий потока.
из уравнения 2.376 на основе условий потока.