Модель дискретных частиц
В модели дискретных частиц поток дисперсной фазы моделируется посредством отслеживания определенного числа частиц в непрерывной фазе жидкости. В Creo Flow Analysis на эту модель накладываются следующие допущения и ограничения:
• Определенное число сферических частиц в течение фазы непрерывного потока жидкости. Частицы определяются как Имеется масса (Has Mass) или Безмассовая (Massless).
• Заданный радиус в позиции выпуска и время определяют размер частицы, который остается неизменным. Взаимодействие между частицами не принимается в расчет.
• Частицы взаимодействуют с потоком жидкости и стеночными границами. Объем частицы не вытесняет жидкость (малообъемные фракции в фазе частиц) и не пересекается с геометрией (частица большего размера проходит через меньший зазор).
• Между непрерывной фазой жидкости и частицами не происходит никакого переноса тепла и массы. Предполагается, что температура частиц совпадает с локальной температурой потока жидкости.
При этих допущениях движение каждой отдельной частицы отслеживается с помощью метода Лагранжа. Для отслеживания формируется набор обыкновенных дифференциальных уравнений относительно времени для каждой частицы, содержащий уравнения для позиции и скорости. Эти уравнения затем интегрируются, чтобы рассчитать реакцию частиц по мере их прохода в области потока. Ниже приведены характеристики метода моделирования частиц в Creo Flow Analysis.
• Модель дискретных частиц соответствует методу Эйлера - Лагранжа. Жидкая фаза рассматривается как континуум посредством решения уравнений непрерывности и Навье - Стокса. Дисперсная фаза решается посредством отслеживания движения каждой отдельной частицы с помощью метода Лагранжа. Часть объема, занимаемая частицами, не включается в расчет непрерывной фазы.
• Частицы, заданные как Безмассовая (Massless), перемещаются с потоком жидкости или следуют линиям тока поля потока. Размер или радиус частицы не влияет на поток или частицы и используется только для отображения.
• Для частиц, заданных как Имеет массу (Has Mass), масса определяется значениями, указанным для радиуса или диаметра определенной частицы и плотности частиц. Силы, действующие на частицу, которые определяют движение частиц, включают силу волочения частиц жидкостью (силу инерции) и силу тяжести. Влияние дисперсионных сил турбуленции на частицы не учитывается. Размер частиц влияет на силы волочения частиц жидкостью и постпроцессинг.
• Обмен импульсом между фазой жидкости и дискретными фазами частиц моделируется следующим образом:
◦ Одностороннее сопряжение (One-way coupling) - на движение частиц влияет только фаза жидкости.
◦ Двустороннее сопряжение (Two-way coupling) - частицы также влияют на поток жидкости посредством силы волочения потока жидкости и частиц.
• Взаимодействия между частицами и стенками моделируются с использованием таких моделей, как прилипание, абсолютное отражение и частичное отражение.
• В то время как фаза жидкости может быть стабильной и нестабильной, отслеживание частиц является нестационарным процессом, который включает интегрирование путей частиц через дискретизированную область. В этом методе отдельные частицы высвобождаются или вводятся из определенных расположений в разные моменты времени. Каждая частица отслеживается от позиции высвобождения до целевого расположения, где она покидает область или достигает определенных пределов интеграции. В завершение выполняется осреднение всех путей частиц и вычисляются взаимодействия между частицами и жидкостью как исходные условия для уравнений импульса фазы жидкости.
• Путь частиц отображается с использованием метода отслеживания относительной траектории в модуле Частица (Particle).
Теория движения частиц
В методе Лагранжа движение частиц определяется по балансу сил, действующих на частицу, и условиям, при которых частица высвобождается (начальные условия). Для моделирования дискретной фазы частиц сначала формируются уравнения движения для частиц на основе баланса сил. Затем задаются граничные и начальные условия для частиц. Наконец, выполняется интегрирование уравнений движения частиц для отслеживания частиц.
Уравнения движения частиц
• Баланс сил, действующих на частицу
Для перемещения частицы в непрерывной жидкой среде движение частицы определяется по результирующей силе, действующей на нее. Согласно второму закону Ньютона, можно выразить баланс сил, действующих на частицу, в следующей формуле Лагранжа:
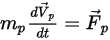
Уравнение 2.366
Здесь
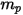 | масса частицы, кг |
 | скорость частицы, м/с |
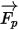 | результирующая сила, действующая на частицу (Н), которая влияет на ускорение частицы |
В декартовой системе координат, если
точка 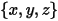 | расположение частицы |
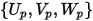 | компоненты скорости частицы |
При использовании метода Лагранжа скорость 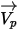 определяется следующим образом:
определяется следующим образом:
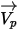 определяется следующим образом:
определяется следующим образом: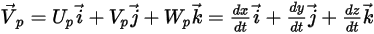
Уравнение 2.367
Для сферической частицы, которая занимает объем 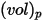 при плотности
при плотности 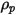 и диаметре
и диаметре 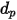 (в качестве входных данных Creo Flow Analysis принимает радиус), масса частицы
(в качестве входных данных Creo Flow Analysis принимает радиус), масса частицы 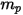 вычисляется следующим образом:
вычисляется следующим образом:
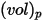 при плотности
при плотности 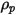 и диаметре
и диаметре 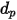 (в качестве входных данных Creo Flow Analysis принимает радиус), масса частицы
(в качестве входных данных Creo Flow Analysis принимает радиус), масса частицы 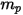 вычисляется следующим образом:
вычисляется следующим образом: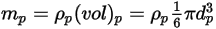
Уравнение 2.368
Как и в случае результирующей силы 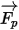 , свой вклад вносят такие факторы, как сила волочения частиц жидкостью, сила тяжести и силы, возникающие при вращении области (центробежная сила и сила Кориолиса). К дополнительным факторам относятся другие силы, связанные с разницей скоростей частицы и жидкости и перемещением жидкости частицей. В Creo Flow Analysis уравнение
, свой вклад вносят такие факторы, как сила волочения частиц жидкостью, сила тяжести и силы, возникающие при вращении области (центробежная сила и сила Кориолиса). К дополнительным факторам относятся другие силы, связанные с разницей скоростей частицы и жидкости и перемещением жидкости частицей. В Creo Flow Analysis уравнение 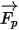 можно выразить следующим образом:
можно выразить следующим образом:
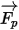 , свой вклад вносят такие факторы, как сила волочения частиц жидкостью, сила тяжести и силы, возникающие при вращении области (центробежная сила и сила Кориолиса). К дополнительным факторам относятся другие силы, связанные с разницей скоростей частицы и жидкости и перемещением жидкости частицей. В Creo Flow Analysis уравнение
, свой вклад вносят такие факторы, как сила волочения частиц жидкостью, сила тяжести и силы, возникающие при вращении области (центробежная сила и сила Кориолиса). К дополнительным факторам относятся другие силы, связанные с разницей скоростей частицы и жидкости и перемещением жидкости частицей. В Creo Flow Analysis уравнение 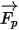 можно выразить следующим образом:
можно выразить следующим образом: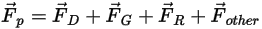
Уравнение 2.369
Здесь
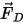 | сила волочения (Н) |
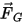 | сила тяжести (Н) |
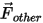 | другие силы, такие как виртуальная массовая сила, сила, обусловленная наличием градиента давления, подъемная сила, заданная пользователем (n) |
По умолчанию учитывается только действующая на частицу сила волочения.
Если подставить уравнение 2.369 в уравнение 2.366 и разделить его на 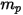 , решенное уравнение баланса сил для частицы примет следующий вид:
, решенное уравнение баланса сил для частицы примет следующий вид:
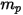 , решенное уравнение баланса сил для частицы примет следующий вид:
, решенное уравнение баланса сил для частицы примет следующий вид: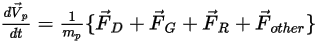
Уравнение 2.370
Чтобы закрыть уравнение 2.370, необходимо рассчитать вклад каждой отдельной силы. Подмодели или формулы, применяемые в Creo Flow Analysis:
◦ Сила волочения частиц
Аэродинамическая сила волочения частицы пропорциональна скорости скольжения фазы, разнице между скоростями жидкости и частицы. Если принять, что скорость потока жидкости в области, в которой находится частица в данный момент времени, равна 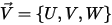 , силу волочения можно выразить следующим образом:
, силу волочения можно выразить следующим образом:
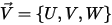 , силу волочения можно выразить следующим образом:
, силу волочения можно выразить следующим образом: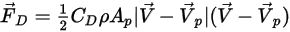
Уравнение 2.371
Здесь
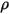 | плотность фазы жидкости |
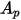 | площадь частицы, проецируемая на направление потока |
Для сферической частицы диаметром 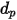
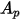 - это максимальная площадь поперечного сечения:
- это максимальная площадь поперечного сечения:
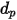
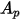 - это максимальная площадь поперечного сечения:
- это максимальная площадь поперечного сечения: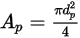
Уравнение 2.372
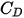 - коэффициент волочения, зависящий от относительного числа Рейнольдса (
- коэффициент волочения, зависящий от относительного числа Рейнольдса (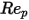 ):
):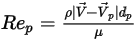
Уравнение 2.373
Здесь 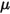 - динамическая вязкость жидкости (Па-с).
- динамическая вязкость жидкости (Па-с).
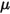 - динамическая вязкость жидкости (Па-с).
- динамическая вязкость жидкости (Па-с).Коэффициент волочения 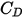 вводится для учета экспериментальных результатов вязкостного волочения твердотельной сферы. Разрабатываются различные модели или эмпирические корреляции для определения функции волочения
вводится для учета экспериментальных результатов вязкостного волочения твердотельной сферы. Разрабатываются различные модели или эмпирические корреляции для определения функции волочения 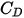 (
(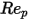 ), чтобы оценить обмен между жидкостью и частицей. Для гладких сферических частиц наиболее полной функцией
), чтобы оценить обмен между жидкостью и частицей. Для гладких сферических частиц наиболее полной функцией 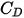 из множества моделей являются исправления Морси и Александера,
из множества моделей являются исправления Морси и Александера,
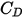 вводится для учета экспериментальных результатов вязкостного волочения твердотельной сферы. Разрабатываются различные модели или эмпирические корреляции для определения функции волочения
вводится для учета экспериментальных результатов вязкостного волочения твердотельной сферы. Разрабатываются различные модели или эмпирические корреляции для определения функции волочения 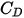 (
(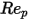 ), чтобы оценить обмен между жидкостью и частицей. Для гладких сферических частиц наиболее полной функцией
), чтобы оценить обмен между жидкостью и частицей. Для гладких сферических частиц наиболее полной функцией 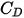 из множества моделей являются исправления Морси и Александера,
из множества моделей являются исправления Морси и Александера,Ссылки: S. A. Morsi and A. J. Alexander, "An Investigation of Particle Trajectories in Two-Phase Flow Systems" (Исследование траекторий частиц в системах двухфазных потоков) (на английском языке), J. Fluid Mech., 55(2) 193–208, September 26 1972 (на английском языке).
имеющие общее выражение:
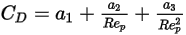
Уравнение 2.374
Здесь 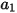 ,
, 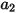 и
и 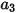 - константы модели, значения которых зависят от относительного числа Рейнольдса, как показано в следующей таблице:
- константы модели, значения которых зависят от относительного числа Рейнольдса, как показано в следующей таблице:
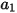 ,
, 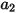 и
и 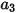 - константы модели, значения которых зависят от относительного числа Рейнольдса, как показано в следующей таблице:
- константы модели, значения которых зависят от относительного числа Рейнольдса, как показано в следующей таблице: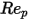 | 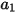 | 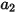 | 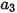 |
0 < 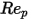 <= 0.1 <= 0.1 | 0 | 24 | 0 |
0.1 < 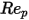 <= 1 <= 1 | 3.690 | 22.73 | 0.0903 |
1 < 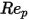 <= 10 <= 10 | 1.222 | 29.1667 | -3.8889 |
10 < 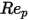 <= 100 <= 100 | 0.6167 | 46.50 | -116.67 |
100 < 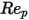 <= 1000 <= 1000 | 0.3644 | 98.33 | -2778 |
1000 < 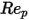 <= 5000 <= 5000 | 0.357 | 148.62 | -47500 |
5000 < 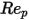 <= 10000 <= 10000 | 0.46 | -490.546 | 578700 |
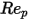 > 10000 > 10000 | 0.5191 | -1662.5 | 5416700 |
Таблица демонстрирует, что при очень малых числах Рейнольдса для частицы (вязкий режим), 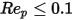 , коэффициент волочения для потока, проходящего через сферические частицы, возвращается к закону Стокса:
, коэффициент волочения для потока, проходящего через сферические частицы, возвращается к закону Стокса:
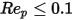 , коэффициент волочения для потока, проходящего через сферические частицы, возвращается к закону Стокса:
, коэффициент волочения для потока, проходящего через сферические частицы, возвращается к закону Стокса:
Уравнение 2.375
Напротив, если значение 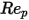 достаточно велико для того, чтобы инерционные эффекты превосходили вязкостные, поток жидкости и частиц находится в инерционном режиме или режиме Ньютона. Из таблицы можно заметить, что коэффициент волочения становится менее зависимым от относительного числа Рейнольдса. Кроме того, константа значения
достаточно велико для того, чтобы инерционные эффекты превосходили вязкостные, поток жидкости и частиц находится в инерционном режиме или режиме Ньютона. Из таблицы можно заметить, что коэффициент волочения становится менее зависимым от относительного числа Рейнольдса. Кроме того, константа значения 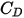 часто используется вместо полной модели Морси и Александера:
часто используется вместо полной модели Морси и Александера:
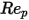 достаточно велико для того, чтобы инерционные эффекты превосходили вязкостные, поток жидкости и частиц находится в инерционном режиме или режиме Ньютона. Из таблицы можно заметить, что коэффициент волочения становится менее зависимым от относительного числа Рейнольдса. Кроме того, константа значения
достаточно велико для того, чтобы инерционные эффекты превосходили вязкостные, поток жидкости и частиц находится в инерционном режиме или режиме Ньютона. Из таблицы можно заметить, что коэффициент волочения становится менее зависимым от относительного числа Рейнольдса. Кроме того, константа значения 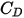 часто используется вместо полной модели Морси и Александера:
часто используется вместо полной модели Морси и Александера: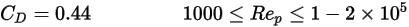
Уравнение 2.376
В переходной области между вязкостным и инерционным режимами, 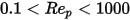 , для сферических частиц важны как вязкостные, так и инерционные эффекты. Поэтому коэффициент волочения является сложной функцией относительного числа Рейнольдса, которую можно оценить с помощью модели Морси и Александера или других корреляций. Например, согласно модели Шиллера и Наумана:
, для сферических частиц важны как вязкостные, так и инерционные эффекты. Поэтому коэффициент волочения является сложной функцией относительного числа Рейнольдса, которую можно оценить с помощью модели Морси и Александера или других корреляций. Например, согласно модели Шиллера и Наумана:
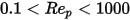 , для сферических частиц важны как вязкостные, так и инерционные эффекты. Поэтому коэффициент волочения является сложной функцией относительного числа Рейнольдса, которую можно оценить с помощью модели Морси и Александера или других корреляций. Например, согласно модели Шиллера и Наумана:
, для сферических частиц важны как вязкостные, так и инерционные эффекты. Поэтому коэффициент волочения является сложной функцией относительного числа Рейнольдса, которую можно оценить с помощью модели Морси и Александера или других корреляций. Например, согласно модели Шиллера и Наумана:Ссылки: L. Schiller and Z. Naumann, "Z. Ver. Deutsch. Ing. 77. 318. 1935.
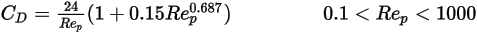
Уравнение 2.377
Чтобы упростить выражение элемента тянущей силы в уравнении 2.370, вводится время релаксации частиц 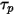 :
:
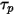 :
: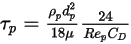
Уравнение 2.378
Если объединить уравнение 2.368, уравнение 2.371, уравнение 2.372, уравнение 2.373 и уравнение 2.378, получится следующая формула для тянущей силы на единицу массы частицы:
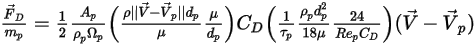
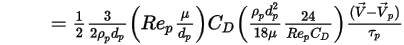
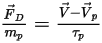
Уравнение 2.379
Таким образом, уравнение баланса сил для частицы по умолчанию (при учете только силы волочения) имеет следующий вид:
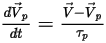
Уравнение 2.380
• Включение элемента силы тяжести
По умолчанию элемент силы тяжести не включен в уравнение баланса сил для частицы. Можно активировать элемент силы тяжести в Creo Flow Analysis. Для частицы, погруженной в поток жидкости, эффект силы тяжести выражается в виде архимедовой силы, равной весу жидкости, вытесняемой частицей. Если 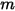 - масса жидкости, вытесняемой частицей, а
- масса жидкости, вытесняемой частицей, а 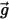 - вектор ускорения свободного падения, результирующая сила имеет следующий вид:
- вектор ускорения свободного падения, результирующая сила имеет следующий вид:
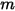 - масса жидкости, вытесняемой частицей, а
- масса жидкости, вытесняемой частицей, а 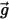 - вектор ускорения свободного падения, результирующая сила имеет следующий вид:
- вектор ускорения свободного падения, результирующая сила имеет следующий вид: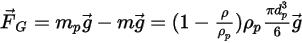
Уравнение 2.381
Или сила на единицу массы частицы выражается следующим образом:
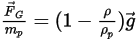
Уравнение 2.382
А уравнение баланса сил получает следующий вид:
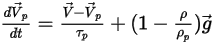
Уравнение 2.383
• Вращающая сила, действующая на частицы
При моделировании потоков жидкости во вращающейся системе отсчета составной частью ускорения частиц является обусловленный вращением дополнительный элемент силы 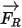 . Он включает эффект силы Кориолиса и центробежной силы:
. Он включает эффект силы Кориолиса и центробежной силы:
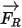 . Он включает эффект силы Кориолиса и центробежной силы:
. Он включает эффект силы Кориолиса и центробежной силы: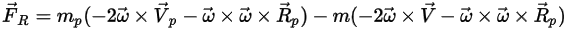
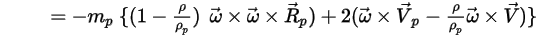
Уравнение 2.384
Или вращающая сила на единицу массы частицы выражается следующим образом:
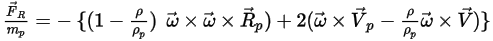
Уравнение 2.385
Здесь
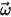 | Угловая скорость вращающейся системы отсчета |
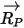 | вектор, соединяющий центр оси и расположение частицы |
После добавления этого элемента силы уравнение баланса для частицы получит следующий вид:
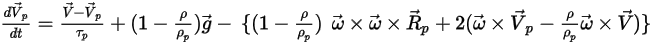
Уравнение 2.386
Уравнение 2.386 описывает движение частицы в системе Лагранжа, когда поток разрешается во вращающейся системе отсчета.
Граничные и начальные условия для частиц
В методе Лагранжа отслеживание частиц является нестационарной процедурой. Поэтому для вычисления траекторий частиц требуются граничные и начальные условия. Граничные условия определяют реакцию частиц на границах расчетной области, особенно при взаимодействиях частиц со стенками. Начальные условия определяют высвобождение частиц от границ, включая позицию выпуска, частоту, скорость, тип и размер (радиус) частиц, а также число частиц.
Граничные условия
Creo Flow Analysis предоставляет граничное условие дискретной фазы для определения реакции частиц у границы. Когда частица достигает границы области потока (включая физическую границу и поверхность раздела твердого тела и жидкости), например стенки или границы впуска, возможен один из следующих вариантов:
• Частица отражается при упругом или неупругом столкновении.
• Частица проходит через границу и теряется для расчета в точке столкновения с границей.
• Частица захватывается стенкой и теряется для расчета в точке столкновения с границей.
• Частица проходит через внутреннюю граничную зону, например вентилятор или пористую мембрану.
• Взаимодействие частиц с границей определяется пользовательскими методами, используемыми для моделирования реакции частицы при столкновении с границей.
На основе реакции частиц у границ граничные условия и поверхности потока перегруппируются в соответствии с тремя типами граничных условий для дискретных частиц: "Открытая" (Open), "Симметричная" (Symmetry) и "Стенка" (Wall).
• Открытая граница для дискретных частиц
Частицы или линии потока могут выходить из области расчета. Открытая граница - это граница на входе или выходе фазы потока жидкости в системе Эйлера. Она также может применяться к границам потока, таким как стенка и симметрия. У открытой границы частица выходит из области или входит в нее, в зависимости от направления скорости частицы.
Пусть  - единичный вектор нормали к открытой границе в направлении из области расчета, а скорость частицы на границе составляет
- единичный вектор нормали к открытой границе в направлении из области расчета, а скорость частицы на границе составляет 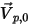 . Если
. Если 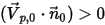 , вектор скорости
, вектор скорости 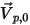 будет направлен из области расчета наружу. Это означает, что частица проходит через границу и теряется для расчета в точке столкновения с границей.
будет направлен из области расчета наружу. Это означает, что частица проходит через границу и теряется для расчета в точке столкновения с границей.
 - единичный вектор нормали к открытой границе в направлении из области расчета, а скорость частицы на границе составляет
- единичный вектор нормали к открытой границе в направлении из области расчета, а скорость частицы на границе составляет 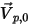 . Если
. Если 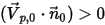 , вектор скорости
, вектор скорости 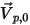 будет направлен из области расчета наружу. Это означает, что частица проходит через границу и теряется для расчета в точке столкновения с границей.
будет направлен из области расчета наружу. Это означает, что частица проходит через границу и теряется для расчета в точке столкновения с границей.• Симметричная граница для частиц
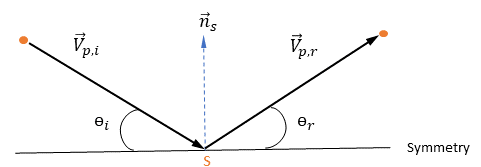
Когда частица или траектория трассирующей частицы в области расчета сталкивается с дискретной симметричной границей, граничное условие отражает частицу обратно в область. В случае фазы дискретных частиц симметричная граница для частиц обычно соответствует симметрии потока в системе Эйлера. Это также может быть место выпуска частиц.
Пусть 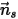 - единичный вектор нормали к симметричной границе в точке
- единичный вектор нормали к симметричной границе в точке 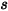 симметрии, который направлен от симметричной границы в область расчета.
симметрии, который направлен от симметричной границы в область расчета. 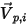 и
и 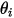 вводятся для определения угла скорости частицы при столкновении частиц с симметричной границей, как показано на следующем рисунке. При отражении от симметричной границы общая кинетическая энергия частицы сохраняется: касательный компонент скорости не меняется, а нормальный компонент скорости просто меняет знак. Симметричное граничное условие для частиц выражается следующим образом:
вводятся для определения угла скорости частицы при столкновении частиц с симметричной границей, как показано на следующем рисунке. При отражении от симметричной границы общая кинетическая энергия частицы сохраняется: касательный компонент скорости не меняется, а нормальный компонент скорости просто меняет знак. Симметричное граничное условие для частиц выражается следующим образом:
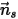 - единичный вектор нормали к симметричной границе в точке
- единичный вектор нормали к симметричной границе в точке 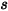 симметрии, который направлен от симметричной границы в область расчета.
симметрии, который направлен от симметричной границы в область расчета. 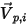 и
и 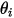 вводятся для определения угла скорости частицы при столкновении частиц с симметричной границей, как показано на следующем рисунке. При отражении от симметричной границы общая кинетическая энергия частицы сохраняется: касательный компонент скорости не меняется, а нормальный компонент скорости просто меняет знак. Симметричное граничное условие для частиц выражается следующим образом:
вводятся для определения угла скорости частицы при столкновении частиц с симметричной границей, как показано на следующем рисунке. При отражении от симметричной границы общая кинетическая энергия частицы сохраняется: касательный компонент скорости не меняется, а нормальный компонент скорости просто меняет знак. Симметричное граничное условие для частиц выражается следующим образом: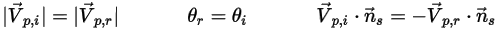
Уравнение 2.387
Здесь
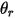 | угол в точке 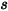 симметрии (град) симметрии (град) |
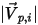 | величина скорости падающей частицы (м/с) |
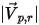 | величина скорости отраженной частицы (м/с) |
• Граница стенки для частиц
В случае жидких капель взаимодействие между каплями и стенкой зависит от температуры, материала и шероховатости стенки, угла и скорости столкновения, наличия пленки на стенке и различных других параметров. В результате для воспроизведения различных режимов взаимодействия между стенкой и частицами и учета влияния параметров потока и условий стеночной границы используется диапазон подмоделей.
В текущей модели дискретных частиц предполагается, что форма, размер и масса частиц остаются неизменными. Кроме того, считается, что жидкость и частицы находятся в тепловом равновесии. Таким образом, простой метод описывает процесс столкновения частиц (имеющих массу) со стенками: в процессе столкновения частицы обмениваются импульсом только со стенкой и используется один из трех способов взаимодействия частиц со стенкой. Это следующие три способа: абсолютное отражение, отражение с прилипанием и частичное отражение.
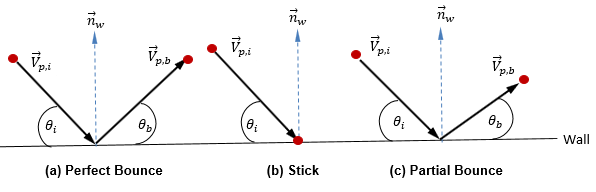
◦ Абсолютное отражение - частица (ее траектория) отражается при столкновении со стенкой. Импульс и кинетическая энергия частицы полностью сохраняются. Угол падения равен углу отражения, а нормальный к стенке компонент скорости меняет знак:
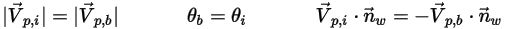
Уравнение 2.388
Здесь
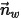 | единичный вектор нормали к стенке |
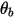 | угол со стеночной границей (град) |
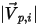 | величина скорости падающей частицы (м/с) |
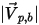 | величина скорости отраженной частицы (м/с) |
◦ Прилипание - частица сталкивается со стенкой, полностью теряет импульс и энергию и прилипает к стенке:

Если не учитывать накопление частиц на стенке, после этого частица полностью теряется для расчета в точке взаимодействия с границей.
◦ Частичное отражение - промежуточный между абсолютным отражением и прилипанием способ взаимодействия частиц со стенкой. Частица (ее траектория) отражается от стенки, но теряет часть энергии в нормальном, в касательном или в обоих направлениях. Импульс и кинетическая энергия частицы не сохраняются, а угол падения обычно больше угла отражения:
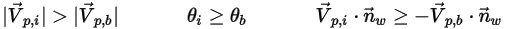
Потеря энергии при взаимодействии частицы со стенкой определяется входными данными пользователя:
▪ Потеря энергии по нормали (Normal Energy Loss) - определяет потерю нормального компонента кинетической энергии частицы у стенки.
▪ Потеря энергии по касательной (Tangential Energy Loss) - определяет потерю касательного компонента кинетической энергии частицы у стенки.
В Creo Flow Analysis поведение частицы (отражение или прилипание) определяется заданными значениями максимальной и минимальной нормальной скорости. Если 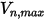 - заданная максимальная нормальная скорость частицы, а
- заданная максимальная нормальная скорость частицы, а 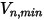 - заданная минимальная нормальная скорость частицы, можно получить следующие условия:
- заданная минимальная нормальная скорость частицы, можно получить следующие условия:
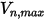 - заданная максимальная нормальная скорость частицы, а
- заданная максимальная нормальная скорость частицы, а 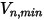 - заданная минимальная нормальная скорость частицы, можно получить следующие условия:
- заданная минимальная нормальная скорость частицы, можно получить следующие условия:▪ Если 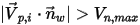 или
или 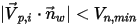 , частица отражается от стенки.
, частица отражается от стенки.
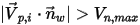 или
или 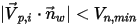 , частица отражается от стенки.
, частица отражается от стенки.▪ Если 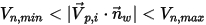 , частица прилипает к стенке.
, частица прилипает к стенке.
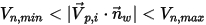 , частица прилипает к стенке.
, частица прилипает к стенке.Модели взаимодействия частиц со стенкой применяются только для частиц с атрибутом Имеется масса (Has Mass). Безмассовые частицы следуют линии потока вдоль стенок.
Имейте в виду, что стеночными границами для частиц могут быть внешние стенки или поверхности раздела твердого тела и жидкости. Как и в случае открытых и симметричных границ, частицы могут выпускаться из стеночной границы.
Начальные условия (выпуск частиц)
Начальные условия предоставляют начальные значения для всех зависимых переменных дискретной фазы, описывающих мгновенные условия для отдельной частицы. Процедура определения начальных условий для отслеживания частиц в системе Лагранжа включает выпуск частиц (частота и распределение) границами (открытая, симметричная, стеночная и интерфейсная) и назначение свойств для каждой частицы.
При активации действия Выпустить частицу (Release Particle) следующие параметры или переменные являются начальными условиями для движения частицы:
Интегрирование уравнений движения частицы
Для отслеживания движения частиц уравнения траектории каждой частицы решаются (интегрируются) аналитически или численно в системе Лагранжа. Уравнения движения из уравнения 2.367 и уравнения 2.386 переписываются следующим образом:

Уравнение 2.391
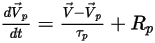
Уравнение 2.392
Здесь
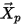 | вектор позиции частицы |
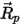 | включает ускорения под действием всех остальных сил, кроме силы волочения, таких как сила тяжести, эффекты вращения и т. д. |
Уравнение 2.391 и уравнение 2.392 представляют набор связанных обыкновенных дифференциальных уравнений. Если заданы начальные и граничные условия смещения частицы, уравнение 2.391 рассчитывается с использованием интегрирования скорости частицы вперед методом Эйлера по временному шагу 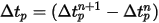 :
:
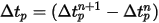 :
: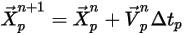
Уравнение 2.393
Здесь
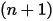 | новые значения |
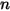 | текущие значения |
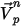 | скорость частицы на текущем временном шаге |
На первом временном шаге,
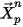 | позиция выпуска |
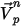 | начальная скорость |
Здесь

Уравнение 2.394
При использовании этого метода прямого интегрирования предполагается, что скорость частицы, рассчитанная в начале временного шага, сохраняется в течение всего шага. В конце временного шага рассчитывается новая скорость частицы путем решения уравнения 2.392 для импульса частицы. Если предположить, что 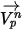 ,
, 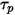 и
и 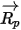 являются постоянными в течение периода времени
являются постоянными в течение периода времени 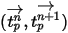 , а свойства жидкости берутся с начала временного шага
, а свойства жидкости берутся с начала временного шага 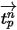 , можно получить аналитическое решение уравнения 2.392:
, можно получить аналитическое решение уравнения 2.392:
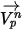 ,
, 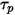 и
и 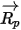 являются постоянными в течение периода времени
являются постоянными в течение периода времени 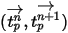 , а свойства жидкости берутся с начала временного шага
, а свойства жидкости берутся с начала временного шага 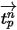 , можно получить аналитическое решение уравнения 2.392:
, можно получить аналитическое решение уравнения 2.392: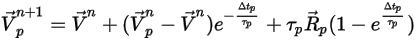
Уравнение 2.395
Чтобы вычислить 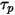 и
и 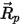 , требуются такие жидкостные переменные, как плотность, вязкость и скорость, в месте нахождения частицы. Они считаются значениями ячейки фазы потока жидкости, в которой в этот момент находится частица. Хотя эта аналитическая схема эффективна, она может становиться неточной при использовании длительных шагов времени и в ситуациях, когда частицы не находятся в гидродинамическом равновесии с непрерывным потоком жидкости. В этом случае используются численные схемы интегрирования уравнения 2.392.
, требуются такие жидкостные переменные, как плотность, вязкость и скорость, в месте нахождения частицы. Они считаются значениями ячейки фазы потока жидкости, в которой в этот момент находится частица. Хотя эта аналитическая схема эффективна, она может становиться неточной при использовании длительных шагов времени и в ситуациях, когда частицы не находятся в гидродинамическом равновесии с непрерывным потоком жидкости. В этом случае используются численные схемы интегрирования уравнения 2.392.
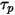 и
и 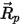 , требуются такие жидкостные переменные, как плотность, вязкость и скорость, в месте нахождения частицы. Они считаются значениями ячейки фазы потока жидкости, в которой в этот момент находится частица. Хотя эта аналитическая схема эффективна, она может становиться неточной при использовании длительных шагов времени и в ситуациях, когда частицы не находятся в гидродинамическом равновесии с непрерывным потоком жидкости. В этом случае используются численные схемы интегрирования уравнения 2.392.
, требуются такие жидкостные переменные, как плотность, вязкость и скорость, в месте нахождения частицы. Они считаются значениями ячейки фазы потока жидкости, в которой в этот момент находится частица. Хотя эта аналитическая схема эффективна, она может становиться неточной при использовании длительных шагов времени и в ситуациях, когда частицы не находятся в гидродинамическом равновесии с непрерывным потоком жидкости. В этом случае используются численные схемы интегрирования уравнения 2.392.Сопряжение частица-жидкость
При использовании метода Эйлера - Лагранжа предполагается, что непрерывный поток жидкости вызывает реакцию частицы в результате действия сил, тепла и переноса массы. Например, элемент силы 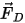 в уравнении 2.370 баланса сил для частицы относится к аэродинамической тянущей силе, прикладываемой потоком к частице. Хотя фаза частиц считается дискретной и не вытесняет жидкость в объеме, частицы могут противодействовать потоку жидкости в результате обмена импульсом и, возможно, массой и теплом. Воздействие частиц на поток называется сопряжением частица-жидкость. Существует две категории:
в уравнении 2.370 баланса сил для частицы относится к аэродинамической тянущей силе, прикладываемой потоком к частице. Хотя фаза частиц считается дискретной и не вытесняет жидкость в объеме, частицы могут противодействовать потоку жидкости в результате обмена импульсом и, возможно, массой и теплом. Воздействие частиц на поток называется сопряжением частица-жидкость. Существует две категории:
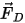 в уравнении 2.370 баланса сил для частицы относится к аэродинамической тянущей силе, прикладываемой потоком к частице. Хотя фаза частиц считается дискретной и не вытесняет жидкость в объеме, частицы могут противодействовать потоку жидкости в результате обмена импульсом и, возможно, массой и теплом. Воздействие частиц на поток называется сопряжением частица-жидкость. Существует две категории:
в уравнении 2.370 баланса сил для частицы относится к аэродинамической тянущей силе, прикладываемой потоком к частице. Хотя фаза частиц считается дискретной и не вытесняет жидкость в объеме, частицы могут противодействовать потоку жидкости в результате обмена импульсом и, возможно, массой и теплом. Воздействие частиц на поток называется сопряжением частица-жидкость. Существует две категории:• Одностороннее сопряжение (One-Way Coupling)
Одностороннее сопряжение позволяет жидкости влиять на траектории частиц, но частицы не оказывают никакого влияния на жидкость. В случае безмассовых частиц взаимодействие частиц с жидкостью является односторонним сопряжением: частицы перемещаются вместе с потоком жидкости. Для частиц, имеющих массу, одностороннее сопряжение может быть приемлемой аппроксимацией в потоках с низкими нагрузками дисперсной фазы, в которых частицы имеют незначительное влияние на поток жидкости.
Для непрерывной фазы жидкости поле потока рассчитывается как однофазный поток жидкости без присутствия фазы дисперсных частиц. Затем движение частиц отслеживается на основе вычисленного поля потока и начальных условий. В случае стационарного потока отслеживание частиц происходит после получения сходящегося решения потока непрерывной фазы посредством решения уравнений непрерывности и Навье - Стокса. В случае моделирования нестационарного потока движения частиц отслеживаются в конце каждого временного шага моделирования потока.
• Двустороннее сопряжение (Two-Way Coupling)
В случае частиц с массой двустороннее сопряжение позволяет жидкости влиять на траектории частиц. Также происходит воздействие частиц на непрерывную фазу жидкости. Без учета передачи массы и тепла двустороннее взаимодействие между жидкостью и частицами включает только обмен импульсом. Передача импульса от непрерывной фазы к дискретной рассчитывается посредством отслеживания импульса, получаемого или теряемого каждой отдельной частицей при прохождении через контрольный объем. При двустороннем сопряжении обмен импульсом между частицами и жидкостью необходимо включать в уравнения импульса жидкости для учета воздействия траекторий дискретной фазы на континуум. В уравнении 2.386 только в тянущей силе учитывается обмен импульсом между частицами и жидкостью и добавляется в уравнения момента. Имейте в виду, что в случае безмассовых частиц взаимодействие между потоком жидкости и частицами не рассчитывается, поэтому траектории дискретной фазы не оказывают никакого влияния на континуум.
Чтобы включить эффекты волочения частиц жидкостью в уравнения импульса непрерывной фазы, тянущую силу для каждой частицы, перемещающейся в потоке, следует применять в контрольном объеме, в котором частицы находятся в течение временного шага. В случае частицы 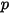 вычисляется источник импульса, связанного с волочением
вычисляется источник импульса, связанного с волочением 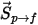 , из следующего дифференциального уравнения:
, из следующего дифференциального уравнения:
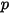 вычисляется источник импульса, связанного с волочением
вычисляется источник импульса, связанного с волочением 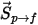 , из следующего дифференциального уравнения:
, из следующего дифференциального уравнения: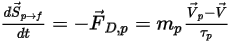
Уравнение 2.396
А источником частиц для непрерывной фазы является элемент источника 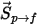 , который умножается на коэффициент расхода потока для этой частицы (массовая скорость потока, деленная на массу частицы):
, который умножается на коэффициент расхода потока для этой частицы (массовая скорость потока, деленная на массу частицы):
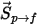 , который умножается на коэффициент расхода потока для этой частицы (массовая скорость потока, деленная на массу частицы):
, который умножается на коэффициент расхода потока для этой частицы (массовая скорость потока, деленная на массу частицы):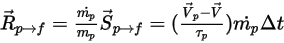
Уравнение 2.397
Здесь
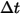 | временной шаг |
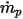 | массовая скорость потока частиц |
Исходя из того, что 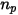 - число частиц, проходящих через контрольный объем в течение временного шага
- число частиц, проходящих через контрольный объем в течение временного шага 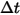 , получаем общий элемент источника частицы-жидкость:
, получаем общий элемент источника частицы-жидкость:
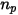 - число частиц, проходящих через контрольный объем в течение временного шага
- число частиц, проходящих через контрольный объем в течение временного шага 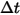 , получаем общий элемент источника частицы-жидкость:
, получаем общий элемент источника частицы-жидкость: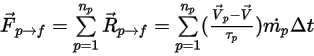
Уравнение 2.398
При добавлении силы волочения частицы жидкостью определяющие уравнения, решенные для непрерывной фазы, теперь выглядят следующим образом:
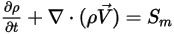
Уравнение 2.399
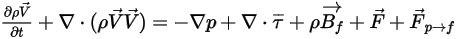
Уравнение 2.400
При одностороннем сопряжении 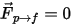 непрерывная фаза жидкости определяется точными однофазными уравнениями непрерывности и импульса. В случае двустороннего сопряжения имеется дополнительный элемент источника тянущей силы частицы-жидкость. Уравнение 2.399 и уравнение 2.400 решаются идентично случаю однофазного потока.
непрерывная фаза жидкости определяется точными однофазными уравнениями непрерывности и импульса. В случае двустороннего сопряжения имеется дополнительный элемент источника тянущей силы частицы-жидкость. Уравнение 2.399 и уравнение 2.400 решаются идентично случаю однофазного потока.
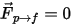 непрерывная фаза жидкости определяется точными однофазными уравнениями непрерывности и импульса. В случае двустороннего сопряжения имеется дополнительный элемент источника тянущей силы частицы-жидкость. Уравнение 2.399 и уравнение 2.400 решаются идентично случаю однофазного потока.
непрерывная фаза жидкости определяется точными однофазными уравнениями непрерывности и импульса. В случае двустороннего сопряжения имеется дополнительный элемент источника тянущей силы частицы-жидкость. Уравнение 2.399 и уравнение 2.400 решаются идентично случаю однофазного потока.