Эйлеровы модели и основные уравнения
В этом разделе объясняются основные уравнения для многофазных моделей объема жидкости (VOF) и смесей, моделирования турбулентности и границ в многофазных потоках.
Главные многофазные основные уравнения
В эйлерово-эйлеровском подходе различные фазы или компоненты в многофазной системе рассматриваются как математически взаимопроникающие континуумы, на которые действует то же давление потока. Поскольку физическое пространство или объем совместно используются всеми фазами, для описания фазового транспорта вводится концепция фазовой объемной доли. Предполагается, что фазовые объемные доли являются непрерывными функциями пространства и времени и их сумма равна единице. Законы сохранения применены для каждой фазы, чтобы получить набор основных уравнений, которые замыкаются теоретическими или эмпирическими материальными уравнениями. В эйлерово-эйлеровском подходе имеется два типа регулярно используемых моделей:
• Неоднородная, или эйлерова, многожидкостная модель - непосредственно решаются основные уравнения для каждой фазы, включая уравнения для импульса, энергии, турбулентности, состава и объемных долей. Взаимодействия между фазами, межфазовые передачи импульса, массы, состава и тепла моделируются физическими подмоделями.
С использованием общего фазового скаляра, ϕq, где q - это q-я фаза, обобщенное уравнение для фазы q имеет следующую вид:
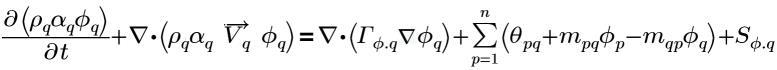
уравнение 2.54
где
ρq | плотность q |
 | скорость |
Sϕq | член источника |
Tϕq | коэффициент диффузии |
αq | объемная доля в q-й фазе |
и ϕq представляет зависимые переменные в многофазной системе:
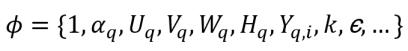
уравнение 2.55
где
Uq, Vq, Wq | компоненты фазовой скорости |
Hq | полная фазовая энтальпия |
Yqi | массовая доля компонента i в q-й фазе |
k | Кинетическая энергия турбуленции |
ε | уровень турбулентного рассеяния кинетический энергии для k–ε моделей |
В уравнении 2.54 второй член на правой стороне представляет межфазовые обмены. В частности,
p | p-я фаза |
n | число фаз в многофазной системе |
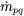 | перенос массы из q-й фазы в p-ю фазу |
θpq | прямой фазовый обмен транспортными количествами, включая импульс, энергию и состав |
С помощью подмоделей для межфазового состава и обмена массой, импульсом и теплом можно получить полный набор основных уравнений потока от транспортных уравнений, которые обобщены здесь.
• Однородная многофазная модель - упрощенная и экономичная альтернатива неоднородной модели. В однородном подходе к моделированию усредняются фазы в основных уравнениях потока, энергии и турбулентности, чтобы получить набор транспортных уравнений смеси, в то время как все еще решаются фазовые объемные доли. Для скаляра смеси, ϕm, обобщенное основное уравнение имеет следующий вид:
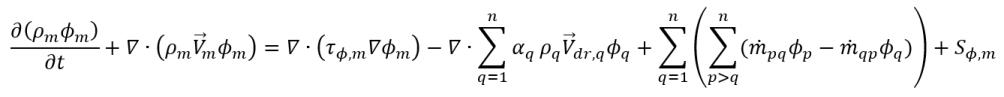
уравнение 2.56
где
m | смесь фаз |
все переменные со смесью m | или усредненными значениями фазы, |
а 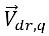 представляет различие между скоростью фазы q и скоростью смеси:
представляет различие между скоростью фазы q и скоростью смеси:
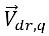 представляет различие между скоростью фазы q и скоростью смеси:
представляет различие между скоростью фазы q и скоростью смеси: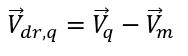
Однородная многофазная модель является предельным случаем эйлерово-эйлеровского многофазного потока, в котором скорость межфазового переноса является высокой. Фундаментальное допущение - все фазы совместно используют то же поле давления. С этим допущением однородная модель затем приводит к упрощению полной неоднородной эйлеровой многожидкостной модели за счет предположения, что все фазы имеют общую скорость, температуру и поле турбулентности. Этот подход является хорошей заменой полной эйлеровой многожидкостной модели из-за простоты реализации и экономии на вычислениях. Физически, без требования моделей межфазового обмена в уравнениях импульса и энергии, может выполняться однородная модель, а также полная многожидкостная модель в таких случаях, как потоки со свободными поверхностями (VOF), кавитация или другие многофазные потоки с высоким уровнем смешивания.
В Creo Flow Analysis текущий многофазный модуль принимает только однородный подход к моделированию. Внимание сосредоточено на моделировании потока со свободной поверхностью (модель объема жидкости) и однородных двухфазных потоков жидкость-газ (модель смеси). В принципе, можно применить возможность моделирования n-фазных потоков.
Многофазные модели VOF и смеси
Многофазные модели объема жидкости (VOF) и смеси используют однородный подход к моделированию. Транспортное уравнение объемной доли в каждой фазе получается из уравнения 2.54. Основные уравнения для импульса и энергии смеси выводятся с помощью уравнения 2.56 и законов сохранения массы, импульса и энергии. Набор основных уравнений представлен в этом разделе.
• Уравнение объемной доли фазы q
В уравнении 2.54, задавая ϕq=1, получаем уравнение для объемной доли фазы q:
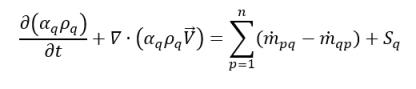
уравнение 2.57
где скорость членов обмена масс 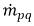 и
и 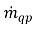 представляет соответственно величину источника и стока для фазы q. В межфазном процессе пеноса массы один из двух членов обычно является нулевым. См. следующий пример.
представляет соответственно величину источника и стока для фазы q. В межфазном процессе пеноса массы один из двух членов обычно является нулевым. См. следующий пример.
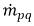 и
и 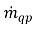 представляет соответственно величину источника и стока для фазы q. В межфазном процессе пеноса массы один из двух членов обычно является нулевым. См. следующий пример.
представляет соответственно величину источника и стока для фазы q. В межфазном процессе пеноса массы один из двух членов обычно является нулевым. См. следующий пример.В процессе испарения жидкая фаза q теряет массу: 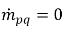 и
и  , тогда как в фазе пара:
, тогда как в фазе пара: 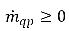 и
и 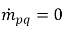 .
.
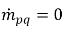 и
и  , тогда как в фазе пара:
, тогда как в фазе пара: 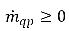 и
и 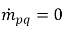 .
.Для n-фазной системы сумма фазовых объемных долей удовлетворяет физическому ограничению:
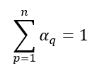
уравнение 2.58
или сохранению суммарной массы:
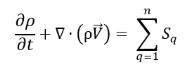
уравнение 2.59
где количественные значения для смеси определяются следующим образом:
◦ Усредненная по объему плотность смеси:
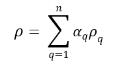
уравнение 2.60
◦ Усредненная по массе скорость смеси:
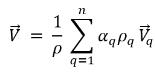
уравнение 2.61
• Уравнение импульса для смеси - получается суммированием отдельных уравнений импульса для всех фаз в системе. Из уравнения 2.56, задавая  , получим
, получим
 , получим
, получим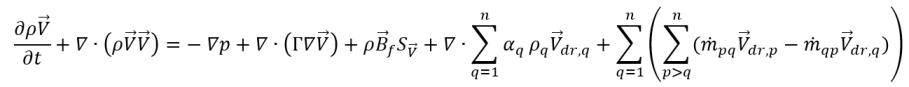
уравнение 2.62
где количественные значения для смеси определяются следующим образом:
◦ Усредненная по объему вязкость смеси:

уравнение 2.63
Коэффициент диффузии Γ в уравнении 2.62 рассчитывается с использованием динамической вязкости смеси μ и турбулентной вязкости μt. Последние два члена на правой стороне представляют прямую передачу импульса и передачу массы, вызванную обменом импульса. Они определяются скоростями фазового дрейфа 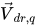 , определенными как:
, определенными как:
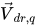 , определенными как:
, определенными как:
уравнение 2.69
В однородном подходе можно моделировать эту скорость дрейфа с помощью алгебраической модели. Однако в текущей модели VOF и смеси предполагается отсутствие скольжения между фазами:
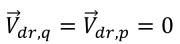
Поэтому оба условия обмена импульса являются нулевыми.
◦ Уравнение энергии смеси
Без скольжения скорости уравнение энергии для смеси принимает следующий вид:
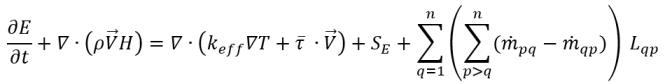
уравнение 2.70
где количественные значения для смеси определяются следующим образом:
▪ Усредненная по объему теплопроводность:
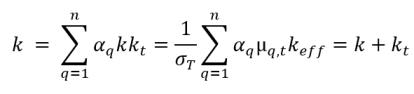
уравнение 2.71
▪ Усредненная по массе энергия смеси и энтальпия:
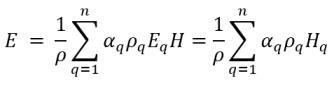
уравнение 2.72
В уравнении 2.70 для энергии смеси член теплоты внутреннего трения 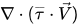 рассчитывается как в едином фазовом потоке, а SE представляет общий внешний или пользовательский тепловой источник.
рассчитывается как в едином фазовом потоке, а SE представляет общий внешний или пользовательский тепловой источник.
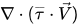 рассчитывается как в едином фазовом потоке, а SE представляет общий внешний или пользовательский тепловой источник.
рассчитывается как в едином фазовом потоке, а SE представляет общий внешний или пользовательский тепловой источник.Последний член на правой стороне - это теплопередача через интерфейс, вызванная передачей массы. В предположении, что фазы имеют одинаковую температуру, Lgp зависит от определения Hq и Hp в решаемом уравнении энергии.
Как описано в модуле Теплота (Heat), статическая энтальпия материала состоит из двух частей: эталонная энтальпия стандартного состояния и физическая энтальпия. В предположении, что фаза q является жидкостью, а фаза p является паром, общие фазовые статические энтальпии имеют вид:
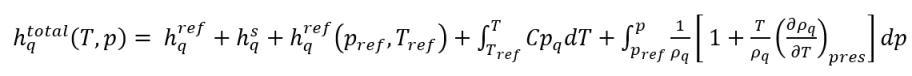
уравнение 2.73
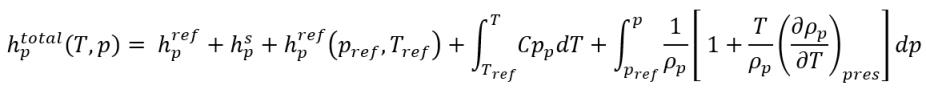
уравнение 2.74
где
pref | Эталонное давление |
Tref | Эталонная температура |
hq,ref | эталонные энтальпии стандартного состояния фазы q |
hp,ref | эталонные энтальпии стандартного состояния фазы p |
Разница эталонных энтальпий
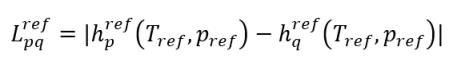
уравнение 2.75
теплота фазового перехода при эталонных температуре Tref и давлении pref.
▪ Включая стандартную эталонную энтальпию:
В уравнении 2.70, если энтальпия H является полной энтальпией смеси, получаем
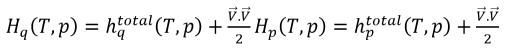
уравнение 2.76
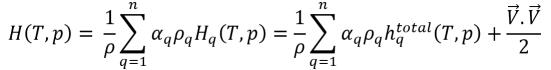
уравнение 2.77
Далее разница энтальпий фазовых формаций или скрытой теплоты, Lpq, уже включена в уравнение энергии. Задано нулевое количество:
Lpq=0
И теплопередача из-за переноса массы, последний член на правой стороне в уравнении 2.70, равняется нулю в уравнении энергии смеси.
▪ Исключение стандартной эталонной энтальпии:
В CFD-решателе полная энтальпия не вычисляется непосредственно. Вместо этого в расчетную энтальпию и внутреннюю энергию включается только явная энтальпия для температуры насыщения:
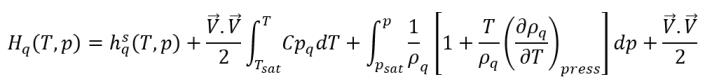
уравнение 2.79
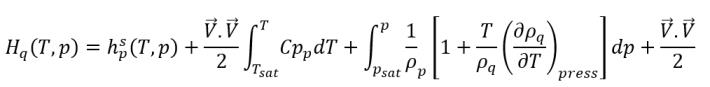
уравнение 2.80
тогда член Lpq не равняется нулю. Он должен представлять скрытую теплоту:
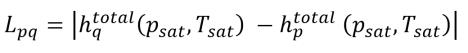
уравнение 2.81
где
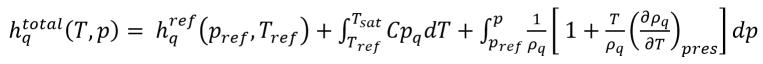
уравнение 2.82
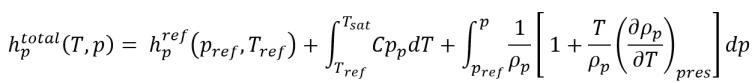
уравнение 2.83
В Creo Flow Analysis по умолчанию автоматически учитывается эталонная энтальпия стандартного состояния. Никакой ввод данных пользователем не требуется.
Модели турбуленции
• Модели турбулентности смеси k-ε
В многофазных моделях объема жидкости (VOF) и смеси эффект турбулентности для смеси фаз описывается с помощью расширений однофазных моделей турбулентности. В Creo Flow Analysis модели турбулентности и пристеночная обработка, описанные в модуле Турбуленция (Turbulence), распространяются на многофазные потоки. Для количественных значений потока смеси стандартные и RNG k–ε модели имеют ту же общую форму, что и в однофазных моделях турбулентности:
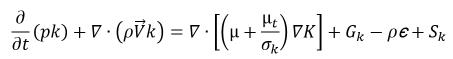
уравнение 2.84
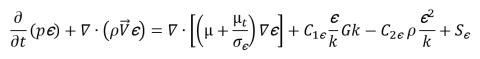
уравнение 2.85
Здесь плотность смеси ρ, 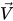 , скорости и молекулярная вязкость μ рассчитываются по соответствующим значениям фазы с помощью уравнений 2.60, 2.61 и 2.63 соответственно; Sk и Sε включают возможные внешние и пользовательские источники, а также источники фазового взаимодействия. Турбулентная вязкость для смеси μt рассчитывается непосредственно из выражения:
, скорости и молекулярная вязкость μ рассчитываются по соответствующим значениям фазы с помощью уравнений 2.60, 2.61 и 2.63 соответственно; Sk и Sε включают возможные внешние и пользовательские источники, а также источники фазового взаимодействия. Турбулентная вязкость для смеси μt рассчитывается непосредственно из выражения:
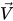 , скорости и молекулярная вязкость μ рассчитываются по соответствующим значениям фазы с помощью уравнений 2.60, 2.61 и 2.63 соответственно; Sk и Sε включают возможные внешние и пользовательские источники, а также источники фазового взаимодействия. Турбулентная вязкость для смеси μt рассчитывается непосредственно из выражения:
, скорости и молекулярная вязкость μ рассчитываются по соответствующим значениям фазы с помощью уравнений 2.60, 2.61 и 2.63 соответственно; Sk и Sε включают возможные внешние и пользовательские источники, а также источники фазового взаимодействия. Турбулентная вязкость для смеси μt рассчитывается непосредственно из выражения: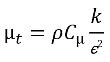
уравнение 2.86
в то время как производство турбулентной кинетической энергии рассчитывается на основе турбулентной вязкости смеси и градиентов скоростей:
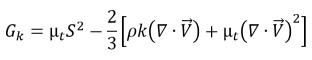
уравнение 2.87
Здесь S представляет модуль средней скорости деформации смеси, 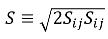
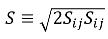
Турбулентная вязкость для фазы q может быть рассчитана как:
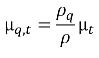
уравнение 2.87
• Эффект турбулентной диффузии
Для многофазных турбулентных течений сила турбулентного рассеяния возникает при усреднении члена мгновенного межфазового трения, который действует аналогично фазовой диффузии. В неоднородной эйлеровой многожидкостной модели этот турбулентный эффект обычно рассматривается как дополнительная межфазовая сила в фазовых уравнениях импульса, которая определяется градиентами фазовых объемных долей. Однако этот турбулентный эффект можно также моделировать непосредственно, рассматривая его как член турбулентной диффузии в фазовых уравнениях объемных долей. Разделив 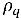 и группируя все источники как
и группируя все источники как 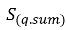 (сумма межфазового переноса массы и внешних массовых источников), получаем следующее управляющее уравнение для объемной доли фазы q в турбулентных потоках:
(сумма межфазового переноса массы и внешних массовых источников), получаем следующее управляющее уравнение для объемной доли фазы q в турбулентных потоках:
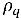 и группируя все источники как
и группируя все источники как 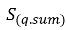 (сумма межфазового переноса массы и внешних массовых источников), получаем следующее управляющее уравнение для объемной доли фазы q в турбулентных потоках:
(сумма межфазового переноса массы и внешних массовых источников), получаем следующее управляющее уравнение для объемной доли фазы q в турбулентных потоках: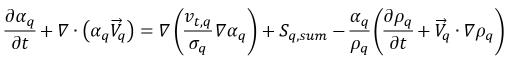
где первый член на правой стороне представляет турбулентную диффузию в фазе q, которая должна отвечать следующему ограничению, чтобы удовлетворялось сохранение общей массы:
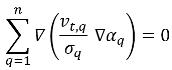
Члены турбулентной диффузии обычно применяются как опция. По умолчанию они не включаются.
Моделирование многофазных границ
В многофазных моделях объема жидкости (VOF) и смеси граничные условия для уравнений потока и энергии совпадают с аналогичными в однофазных потоках. Они описаны в модулях Поток (Flow) и "Теплота" (Heat). Для фазовых долей объема только фиксированные значения и нулевой градиент применяются в следующих случаях:
• Входная граница n-й фазы
Для (n–1) фаз входные объемные доли являются предопределенными, тогда как n-я фаза получается с использованием физического ограничения:
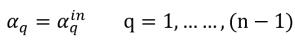
уравнение 2.88
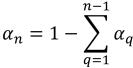
уравнение 2.89
И объемная доля каждой фазы должна быть неотрицательной.
• "Выход"/"Симметрия"/"Граничная стенка"
Для (n–1) фаз условия нулевого градиента применяются для всего выхода, симметрии и границ на стенках, тогда как n-я фаза получается с использованием физического ограничения:
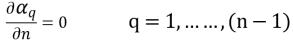
уравнение 2.90
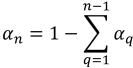
уравнение 2.91
Вышеупомянутые основные уравнения, модели турбулентности и граничные условия формируют основу однородных многофазных моделей VOF и смеси. Без внешних или пользовательских членов с источниками и межфазового переноса массы они представляют замкнутую систему уравнений и решаются численно с помощью основанного на давлении многофазного решателя для конечного объема. Во многих практических приложениях требуются некоторые специализированные подмодели, такие как учет силы поверхностного натяжения в моделях VOF и межфазовый перенос массы, чтобы точно описывать соответствующие физические явления и процессы. Поэтому вместо того чтобы включать подмодели во внешние или пользовательские источники, рекомендуется включать их непосредственно во встроенные модели.