불연속 입자 모델
불연속 입자 모델에서는 연속 유체 위상을 통해 지정된 수의 입자를 추적하여 분산 위상의 흐름이 모델링됩니다. Creo Flow Analysis에서는 모델에 다음과 같은 가정과 제한이 있습니다.
• 연속 유체 위상을 통해 구형 입자 수를 정의합니다. 입자는 질량 있음(Has Mass)이나 질량 없음(Massless)으로 정의됩니다.
• 방출 위치와 시간의 지정된 반지름이 입자 크기를 결정하며 이 크기는 변경되지 않습니다. 입자-입자 상호 작용은 무시할 수 있습니다.
• 입자는 유체 흐름 및 벽 경계와 상호 작용합니다. 입자의 부피는 유체(입자 위상의 낮은 부피 분율)를 대체하거나 형상(오버사이즈 입자가 더 작은 간격에 적합)과 상호 작용하지 않습니다.
• 연속 유체 위상과 입자 사이에 열 및 질량 전달이 발생하지 않습니다. 입자 온도는 유체 흐름의 국소 온도와 같다고 가정합니다.
이 가정 하에, 라그랑주 접근법을 사용하여 개별 입자의 동작을 각각 추적합니다. 때맞춰 각 입자에 대해 위치와 속도의 방정식으로 이루어지는 상미분 방정식을 만들어 추적이 이루어집니다. 그러면 입자가 흐름 도메인을 트래버스할 때 입자의 반응을 계산하기 위해 이 방정식이 통합됩니다. Creo Flow Analysis의 입자 모델링 접근법 특성은 다음과 같습니다.
• 불연속 입자 모델은 오일러 라그랑주 접근법을 따릅니다. 연속성 및 나비어-스톡스 방정식을 풀어 유체 위상이 연속체로 처리됩니다. 라그랑주 접근법을 사용해 각 개별 입자의 동작을 추적하여 분산 위상을 해결합니다. 입자가 차지한 부피 분율은 연속 위상 계산에 포함되지 않습니다.
• 질량 없음(Massless)으로 설정된 입자는 유체 흐름과 함께 이동하거나 흐름장의 유선을 따릅니다. 입자 크기나 반지름은 흐름이나 입자에 영향을 주지 않으며 디스플레이 전용입니다.
• 질량 있음(Has Mass)으로 설정된 입자는 입자 반지름이나 지름 및 입자 밀도에 지정한 값에 의해 질량이 결정됩니다. 입자에 가해지는 힘은 입자의 동작을 결정하며 입자와 유체의 항력(관성력)과 중력을 포함합니다. 입자에 대한 터뷸런스 분산력은 고려되지 않습니다. 입자 크기는 입자와 유체의 항력과 포스트 프로세싱에 영향을 줍니다.
• 유체 위상과 불연속 입자 위상 사이의 운동량 교환이 다음과 같이 모델링됩니다.
◦ 단방향 결합 - 유체 위상만 입자의 동작에 영향을 미칩니다.
◦ 양방향 결합 - 입자도 입자와 유체의 항력을 통해 유체 흐름에 영향을 미칩니다.
• 고정, 완전 바운스 및 부분 바운스와 같은 입자 벽 모델을 사용하여 벽-입자 상호 작용이 모델링됩니다.
• 유체 위상은 안정적일 수도 불안정할 수도 있지만 입자 추적은 분할된 도메인을 통해 입자 경로 통합을 포함하는 과도 프로세스입니다. 이 접근법에서는 개별 입자가 다른 시간의 지정된 위치에서 방출되거나 주입됩니다. 각 입자는 방출 위치에서 대상까지 추적되며 이때 도메인을 벗어나거나 특정한 통합 제한을 충족합니다. 마지막으로, 모든 입자 추적 평균을 구하고, 유체 위상 운동량 방정식에 대한 소스 항으로 입자와 유체의 상호 작용을 계산합니다.
• 입자(Particle) 모듈에서 관련 흐름맥 추적 방법을 사용하여 입자가 이동한 경로가 나타납니다.
입자 동작 이론
라그랑주 접근법에서는 입자의 힘 균형과 입자가 방출되는 조건(초기 조건)에 의해 입자 동작이 결정됩니다. 불연속 입자 위상을 모델링하기 위해 먼저 힘 균형에 따라 입자의 동작 방정식이 구성됩니다. 그런 다음 입자의 경계와 초기 조건을 지정합니다. 마지막으로, 입자 추적을 위해 동작의 입자 방정식 통합이 이루어집니다.
입자 동작의 방정식
• 입자 힘 균형
연속 유체 매체에서 이동하는 불연속 입자의 경우 작용하는 알짜 힘에 의해 입자 동작이 결정됩니다. 뉴턴의 두 번째 법칙에 따라 다음의 라그랑주 형식으로 입자의 힘 균형을 나타낼 수 있습니다.
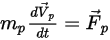
방정식 2.366
여기서 각 항목은 다음을 나타냅니다.
 | 입자 질량 kg |
 | 입자 속도 m/s |
 | 입자 가속도에 영향을 주며 입자에 발효되는 알짜 힘(N) |
카티시안 좌표계에서
점 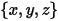 | 입자 위치 |
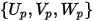 | 입자 속도 컴포넌트 |
라그랑주 접근법을 사용하면 입자 속도 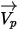 가 다음과 같이 정의됩니다.
가 다음과 같이 정의됩니다.
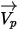 가 다음과 같이 정의됩니다.
가 다음과 같이 정의됩니다.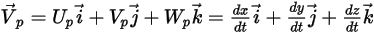
방정식 2.367
밀도 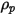 및 지름
및 지름 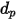 (Creo Flow Analysis에서는 입력으로 반지름 허용)과 함께 부피
(Creo Flow Analysis에서는 입력으로 반지름 허용)과 함께 부피 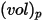 를 차지하는 구형 입자의 경우 입자 질량
를 차지하는 구형 입자의 경우 입자 질량 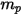 이 다음과 같이 계산됩니다.
이 다음과 같이 계산됩니다.
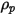 및 지름
및 지름 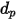 (Creo Flow Analysis에서는 입력으로 반지름 허용)과 함께 부피
(Creo Flow Analysis에서는 입력으로 반지름 허용)과 함께 부피 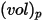 를 차지하는 구형 입자의 경우 입자 질량
를 차지하는 구형 입자의 경우 입자 질량 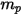 이 다음과 같이 계산됩니다.
이 다음과 같이 계산됩니다.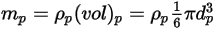
방정식 2.368
알짜 힘 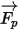 의 경우, 유체와 입자의 항력, 중력 효과 및 도메인 회전으로 인한 힘(구심력 및 코리올리 힘) 등의 기여 요소. 입자와 유체 간의 속도 차이와 입자에 의한 유체의 변위로 인해 다른 힘이 더 작용하기도 합니다. Creo Flow Analysis에서는
의 경우, 유체와 입자의 항력, 중력 효과 및 도메인 회전으로 인한 힘(구심력 및 코리올리 힘) 등의 기여 요소. 입자와 유체 간의 속도 차이와 입자에 의한 유체의 변위로 인해 다른 힘이 더 작용하기도 합니다. Creo Flow Analysis에서는 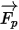 을 다음과 같이 표현할 수 있습니다.
을 다음과 같이 표현할 수 있습니다.
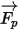 의 경우, 유체와 입자의 항력, 중력 효과 및 도메인 회전으로 인한 힘(구심력 및 코리올리 힘) 등의 기여 요소. 입자와 유체 간의 속도 차이와 입자에 의한 유체의 변위로 인해 다른 힘이 더 작용하기도 합니다. Creo Flow Analysis에서는
의 경우, 유체와 입자의 항력, 중력 효과 및 도메인 회전으로 인한 힘(구심력 및 코리올리 힘) 등의 기여 요소. 입자와 유체 간의 속도 차이와 입자에 의한 유체의 변위로 인해 다른 힘이 더 작용하기도 합니다. Creo Flow Analysis에서는 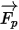 을 다음과 같이 표현할 수 있습니다.
을 다음과 같이 표현할 수 있습니다.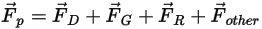
방정식 2.369
여기서 각 항목은 다음을 나타냅니다.
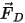 | 항력(N) |
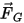 | 중력(N) |
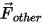 | 가상 질량 힘, 압력 경도력, 사용자가 지정한 양력 등 다른 힘(n) |
기본적으로 입자에 대한 항력만 고려합니다.
방정식 2.369를 방정식 2.366으로 대체하고 이를 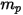 으로 나누면 입자에 대한 풀이된 힘 균형 방정식의 형식은 다음과 같습니다.
으로 나누면 입자에 대한 풀이된 힘 균형 방정식의 형식은 다음과 같습니다.
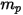 으로 나누면 입자에 대한 풀이된 힘 균형 방정식의 형식은 다음과 같습니다.
으로 나누면 입자에 대한 풀이된 힘 균형 방정식의 형식은 다음과 같습니다.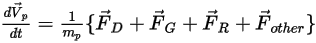
방정식 2.370
방정식 2.370을 닫으려면 개별 힘 각각의 기여도를 계산해야 합니다. Creo Flow Analysis에 사용되는 서브모델 또는 공식은 다음과 같습니다.
◦ 입자에 대한 항력
입자에 대한 공기 항력은 유체 속도와 입자 속도의 차이인 위상 슬립 속도에 비례합니다. 주어진 시간에 입자가 있는 동일한 공간에서 유체 흐름 속도가 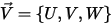 과 같다고 가정하면 항력이 다음과 같이 표현됩니다.
과 같다고 가정하면 항력이 다음과 같이 표현됩니다.
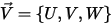 과 같다고 가정하면 항력이 다음과 같이 표현됩니다.
과 같다고 가정하면 항력이 다음과 같이 표현됩니다.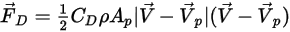
방정식 2.371
여기서 각 항목은 다음을 나타냅니다.
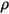 | 유체 위상 밀도 |
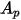 | 진행 방향으로 투영되는 입자의 면적 |
지름이 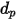 인 구형 입자의 경우
인 구형 입자의 경우 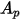 은 횡단면의 최대 면적입니다.
은 횡단면의 최대 면적입니다.
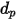 인 구형 입자의 경우
인 구형 입자의 경우 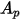 은 횡단면의 최대 면적입니다.
은 횡단면의 최대 면적입니다.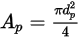
방정식 2.372
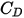 는 항력 계수이며, 상대적 레이놀즈 수
는 항력 계수이며, 상대적 레이놀즈 수 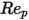 에 의존합니다.
에 의존합니다.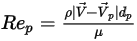
방정식 2.373
여기서 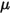 은 유체의 역학 점도입니다(Pa-s).
은 유체의 역학 점도입니다(Pa-s).
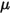 은 유체의 역학 점도입니다(Pa-s).
은 유체의 역학 점도입니다(Pa-s).항력 계수 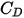 는 구체의 점성 저항에 대한 실험 결과를 설명하고자 도입되었습니다. 저항 기능
는 구체의 점성 저항에 대한 실험 결과를 설명하고자 도입되었습니다. 저항 기능 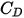 (
(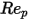 )을 결정하여 유체-입자 교환을 추정하기 위해 다양한 모델과 상관 관계식이 개발되었습니다. 부드러운 구형 입자의 경우 여러 모델 중에서 가장 완전한
)을 결정하여 유체-입자 교환을 추정하기 위해 다양한 모델과 상관 관계식이 개발되었습니다. 부드러운 구형 입자의 경우 여러 모델 중에서 가장 완전한 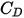 기능은 모르시와 알렉산더의 상관 관계식입니다.
기능은 모르시와 알렉산더의 상관 관계식입니다.
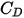 는 구체의 점성 저항에 대한 실험 결과를 설명하고자 도입되었습니다. 저항 기능
는 구체의 점성 저항에 대한 실험 결과를 설명하고자 도입되었습니다. 저항 기능 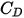 (
(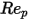 )을 결정하여 유체-입자 교환을 추정하기 위해 다양한 모델과 상관 관계식이 개발되었습니다. 부드러운 구형 입자의 경우 여러 모델 중에서 가장 완전한
)을 결정하여 유체-입자 교환을 추정하기 위해 다양한 모델과 상관 관계식이 개발되었습니다. 부드러운 구형 입자의 경우 여러 모델 중에서 가장 완전한 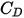 기능은 모르시와 알렉산더의 상관 관계식입니다.
기능은 모르시와 알렉산더의 상관 관계식입니다.참고 문헌: S. A. Morsi and A. J. Alexander, "An Investigation of Particle Trajectories in Two-Phase Flow Systems", J. Fluid Mech., 55(2) 193–208, September 26 1972.
일반 표현식은 다음과 같습니다.
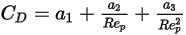
방정식 2.374
여기서 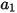 ,
, 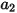 및
및 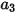 은 모델 상수이고, 그 값은 다음 표에 나온 대로 상대적 레이놀즈 수에 의존합니다.
은 모델 상수이고, 그 값은 다음 표에 나온 대로 상대적 레이놀즈 수에 의존합니다.
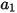 ,
, 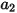 및
및 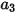 은 모델 상수이고, 그 값은 다음 표에 나온 대로 상대적 레이놀즈 수에 의존합니다.
은 모델 상수이고, 그 값은 다음 표에 나온 대로 상대적 레이놀즈 수에 의존합니다.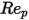 | 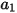 | 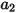 | 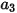 |
0 < 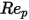 <=0.1 <=0.1 | 0 | 24 | 0 |
0.1 < 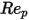 <=1 <=1 | 3.690 | 22.73 | 0.0903 |
1< 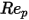 <=10 <=10 | 1.222 | 29.1667 | -3.8889 |
10 < 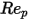 <=100 <=100 | 0.6167 | 46.50 | -116.67 |
100 < 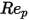 <=1000 <=1000 | 0.3644 | 98.33 | -2778 |
1000 < 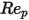 <=5000 <=5000 | 0.357 | 148.62 | -47500 |
5000 < 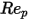 <=10000 <=10000 | 0.46 | -490.546 | 578700 |
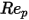 >10000 >10000 | 0.5191 | -1662.5 | 5416700 |
이 표에서는 입자 레이놀즈 수가 매우 낮을 때(점성 상황) 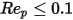 구형 입자를 지나는 흐름의 항력 계수가 스톡스 법칙으로 돌아간다는 것을 보여줍니다.
구형 입자를 지나는 흐름의 항력 계수가 스톡스 법칙으로 돌아간다는 것을 보여줍니다.
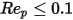 구형 입자를 지나는 흐름의 항력 계수가 스톡스 법칙으로 돌아간다는 것을 보여줍니다.
구형 입자를 지나는 흐름의 항력 계수가 스톡스 법칙으로 돌아간다는 것을 보여줍니다.
방정식 2.375
반대로, 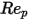 이 충분히 커서 관성 효과가 점성 효과를 지배할 때는 유체-입자 흐름이 관성 또는 뉴턴 상황에 있습니다. 표에서는 상대적 레이놀즈 수에 대한 항력 계수의 의존이 줄어드는 것이 보입니다. 또한 전체 모르시와 알렉산더 모델 대신
이 충분히 커서 관성 효과가 점성 효과를 지배할 때는 유체-입자 흐름이 관성 또는 뉴턴 상황에 있습니다. 표에서는 상대적 레이놀즈 수에 대한 항력 계수의 의존이 줄어드는 것이 보입니다. 또한 전체 모르시와 알렉산더 모델 대신 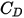 값의 상수가 종종 사용됩니다.
값의 상수가 종종 사용됩니다.
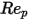 이 충분히 커서 관성 효과가 점성 효과를 지배할 때는 유체-입자 흐름이 관성 또는 뉴턴 상황에 있습니다. 표에서는 상대적 레이놀즈 수에 대한 항력 계수의 의존이 줄어드는 것이 보입니다. 또한 전체 모르시와 알렉산더 모델 대신
이 충분히 커서 관성 효과가 점성 효과를 지배할 때는 유체-입자 흐름이 관성 또는 뉴턴 상황에 있습니다. 표에서는 상대적 레이놀즈 수에 대한 항력 계수의 의존이 줄어드는 것이 보입니다. 또한 전체 모르시와 알렉산더 모델 대신 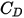 값의 상수가 종종 사용됩니다.
값의 상수가 종종 사용됩니다.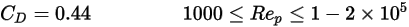
방정식 2.376
점성 상황과 관성 상황 사이의 과도 상황에서(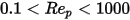 ) 구형 입자에는 점성 효과와 관성 효과 모두 중요합니다. 따라서 항력 계수는 상대적 레이놀즈 수의 복소함수이며 모르시 및 알렉산더 모델이나 다른 상관 관계식으로 추정할 수 있습니다. 예를 들어, 실러와 노만 모델에 따르면 다음과 같습니다.
) 구형 입자에는 점성 효과와 관성 효과 모두 중요합니다. 따라서 항력 계수는 상대적 레이놀즈 수의 복소함수이며 모르시 및 알렉산더 모델이나 다른 상관 관계식으로 추정할 수 있습니다. 예를 들어, 실러와 노만 모델에 따르면 다음과 같습니다.
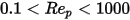 ) 구형 입자에는 점성 효과와 관성 효과 모두 중요합니다. 따라서 항력 계수는 상대적 레이놀즈 수의 복소함수이며 모르시 및 알렉산더 모델이나 다른 상관 관계식으로 추정할 수 있습니다. 예를 들어, 실러와 노만 모델에 따르면 다음과 같습니다.
) 구형 입자에는 점성 효과와 관성 효과 모두 중요합니다. 따라서 항력 계수는 상대적 레이놀즈 수의 복소함수이며 모르시 및 알렉산더 모델이나 다른 상관 관계식으로 추정할 수 있습니다. 예를 들어, 실러와 노만 모델에 따르면 다음과 같습니다.참고 문헌: L. Schiller and Z. Naumann, "Z. Ver. Deutsch. Ing. 77. 318. 1935.
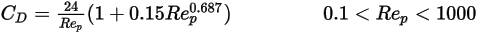
방정식 2.377
방정식 2.370에서 항력 항의 식을 간소화하기 위해 미립자 완화 시간 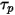 이 도입되었습니다.
이 도입되었습니다.
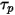 이 도입되었습니다.
이 도입되었습니다.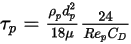
방정식 2.378
방정식 2.368, 방정식 2.371, 방정식 2.372, 방정식 2.373 및 방정식 2.378을 결합하면 단위 입자 질량당 항력에 다음 공식이 생깁니다.
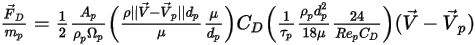
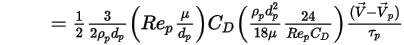
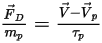
방정식 2.379
따라서 기본(항력만 고려) 입자 힘 균형 방정식은 다음과 같이 표현됩니다.
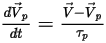
방정식 2.380
• 중력 항 포함
기본적으로 입자 힘 균형 방정식에는 중력 항이 포함되지 않습니다. Creo Flow Analysis에서 중력 항을 활성화해야 합니다. 유체 흐름에 들어간 입자의 경우 중력의 효과로 인해, 입자가 대체한 유체의 무게와 부력이 같아집니다. 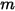 이 입자가 대체한 유체 질량이고
이 입자가 대체한 유체 질량이고 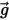 이 중력 벡터라고 가정할 때 결과 힘은 다음과 같습니다.
이 중력 벡터라고 가정할 때 결과 힘은 다음과 같습니다.
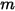 이 입자가 대체한 유체 질량이고
이 입자가 대체한 유체 질량이고 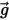 이 중력 벡터라고 가정할 때 결과 힘은 다음과 같습니다.
이 중력 벡터라고 가정할 때 결과 힘은 다음과 같습니다.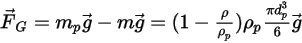
방정식 2.381
또는 단위 입자 질량당 힘은 다음과 같습니다.
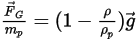
방정식 2.382
또한 힘 균형 방정식은 다음과 같습니다.
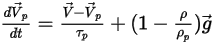
방정식 2.383
• 입자에 대한 회전력
회전 참조 프레임에 있는 모델 유체 흐름의 경우 회전으로 유도된 추가 힘 항 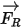 이 입자 가속도의 고유한 부분입니다. 또한 코리올리 힘과 구심력의 효과로 이루어집니다.
이 입자 가속도의 고유한 부분입니다. 또한 코리올리 힘과 구심력의 효과로 이루어집니다.
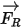 이 입자 가속도의 고유한 부분입니다. 또한 코리올리 힘과 구심력의 효과로 이루어집니다.
이 입자 가속도의 고유한 부분입니다. 또한 코리올리 힘과 구심력의 효과로 이루어집니다.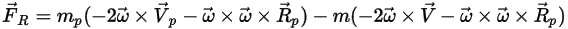
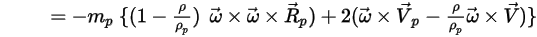
방정식 2.384
또는 단위 입자 질량당 회전력은 다음과 같습니다.
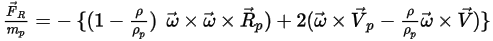
방정식 2.385
여기서 각 항목은 다음을 나타냅니다.
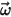 | 회전 참조 프레임의 각속도 |
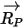 | 축 중심과 입자 위치를 연결하는 벡터 |
이 힘 항이 추가되면 입자 균형 방정식은 다음과 같습니다.
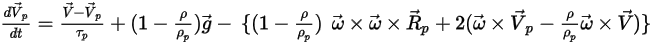
방정식 2.386
방정식 2.386은 흐름이 회전 참조 프레임에서 해결될 때 라그랑주 시스템에서의 입자 동작을 제어합니다.
입자의 경계 및 초기 조건
라그랑주 접근법에서 입자 추적은 과도 절차입니다. 따라서 입자의 궤적을 계산하려면 경계와 초기 조건이 필요합니다. 경계 조건은 특히 입자-벽 상호 작용의 계산 도메인 경계에서 입자 반응을 정의합니다. 초기 조건은 방출 위치, 빈도, 속도, 입자 유형 및 크기(반지름) 및 입자 수를 포함하여 경계의 입자 방출을 결정합니다.
경계 조건
Creo Flow Analysis는 불연속 위상 경계 조건을 제공하여 경계에서 입자 반응을 결정합니다. 입자가 벽이나 유입구 경계와 같은 흐름 도메인(물리적 경계 및 솔리드-유체 인터페이스 포함)에 도달하면 다음 중 하나가 발생합니다.
• 탄성 또는 비탄성 충돌을 통해 입자가 반사됩니다.
• 입자가 경계를 벗어나며 경계에 충격이 가해진 시점에 계산에서 손실됩니다.
• 입자가 벽에 갇히고 경계에 충격이 가해진 시점에 계산에서 손실됩니다.
• 입자가 팬이나 투과성 점프 등의 내부 경계 구역을 통과합니다.
• 경계에 부딪힐 때 입자 반응을 모델링하기 위해 사용자가 정의한 방법으로 입자-경계 상호 작용이 결정됩니다.
경계의 입자 반응에 따라 흐름 경계 조건과 인터페이스가 세 가지 유형의 불연속 입자 경계 조건(개방, 대칭 및 벽)으로 다시 그룹화됩니다.
• 개방 불연속 입자 경계
입자 또는 유선이 계산 도메인을 나갈 수 있습니다. 개방 경계는 오일러 시스템에서 유체 흐름 위상의 유입구 또는 배출구 경계입니다. 벽, 대칭 같은 흐름 경계에도 적용될 수 있습니다. 개방 입자 경계에서 입자 속도 방향에 따라 입자가 도메인을 나가거나 들어옵니다.
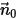 이 입자 경계 속도
이 입자 경계 속도 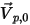 로 계산 도메인에서 떨어진 방향으로 향하는 개방 경계에 대한 단위 수직 벡터가 되게 하십시오.
로 계산 도메인에서 떨어진 방향으로 향하는 개방 경계에 대한 단위 수직 벡터가 되게 하십시오. 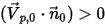 일 경우 속도 벡터
일 경우 속도 벡터 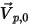 는 계산 도메인에서 멀어집니다. 이는 입자가 경계를 벗어나며 경계에 충격이 가해진 시점에 계산에서 손실됨을 나타냅니다.
는 계산 도메인에서 멀어집니다. 이는 입자가 경계를 벗어나며 경계에 충격이 가해진 시점에 계산에서 손실됨을 나타냅니다.• 대칭 입자 경계
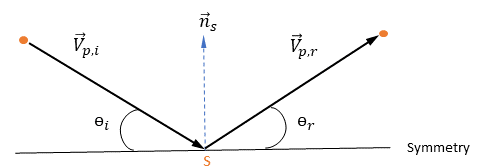
계산 도메인의 입자나 흐름맥이 불연속 대칭 경계에 부딪히면 경계 조건이 도메인으로 해당 입자나 흐름맥을 다시 반사합니다. 불연속 입자 위상의 경우 대칭 입자 경계가 대개 오일러 시스템의 흐름 대칭에 해당합니다. 입자 방출 위치일 수도 있습니다.
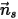 이 대칭에서 계산 도메인 방향으로 대칭의
이 대칭에서 계산 도메인 방향으로 대칭의 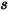 점에서 수직-대칭 단위 벡터가 되게 하십시오. 다음 그림과 같이 입자 대칭 경계의 입자 충격 속도 각을 나타내기 위해
점에서 수직-대칭 단위 벡터가 되게 하십시오. 다음 그림과 같이 입자 대칭 경계의 입자 충격 속도 각을 나타내기 위해 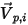 및
및 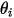 이 도입되었습니다. 입자가 대칭에서 반사되므로 총 운동 에너지가 보존됩니다. 수직 속도 컴포넌트는 기호만 변경하고 탄젠트 속도는 그대로 유지됩니다. 입자 대칭 경계 조건은 다음과 같이 표현됩니다.
이 도입되었습니다. 입자가 대칭에서 반사되므로 총 운동 에너지가 보존됩니다. 수직 속도 컴포넌트는 기호만 변경하고 탄젠트 속도는 그대로 유지됩니다. 입자 대칭 경계 조건은 다음과 같이 표현됩니다.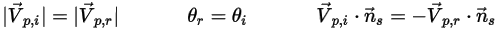
방정식 2.387
여기서 각 항목은 다음을 나타냅니다.
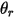 | 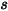 점의 각도: 대칭(도) 점의 각도: 대칭(도) |
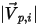 | 입자 입사 속도 크기(m/s) |
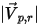 | 입사 반사 속도 크기(m/s) |
• 벽 입자 경계
액체 액적의 경우 액적-벽 상호 작용은 벽 온도, 벽 재료 및 미세도, 충격 각도 및 충격 속도, 벽 필름 유무, 기타 여러 가지 매개 변수에 따라 결정됩니다. 따라서 벽-입자 상호 작용의 여러 가지 상황을 재현하고 흐름 매개 변수와 벽 경계 조건의 영향을 설명하기 위해 다양한 서브모델이 사용됩니다.
현재 불연속 입자 모델에서는 입자의 형태, 크기 및 질량이 그대로 유지된다고 가정합니다. 또한 유체와 입자가 열 평형 상태라고 가정합니다. 따라서 질량을 가진 입자가 벽에 충돌하는 과정을 간단하게 설명할 수 있습니다. 충돌 과정에서 입자는 벽하고만 운동량을 교환하며 세 가지 방법 중 하나로 벽과 상호 작용할 수 있습니다. 완전 바운스, 고정 바운스 및 부분 바운스가 그 방법입니다.
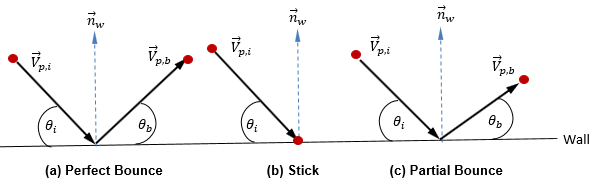
◦ 완전 바운스 - 입자나 흐름맥이 벽에 부딪히면 반사됩니다. 입자의 운동량과 운동 에너지는 완전히 보존됩니다. 입사각은 반사각과 같으며, 벽 수직 속도 컴포넌트의 기호가 바뀝니다.
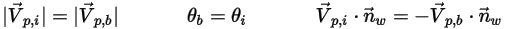
방정식 2.388
여기서 각 항목은 다음을 나타냅니다.
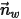 | 벽 수직 단위 벡터 |
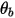 | 벽 경계의 각도(도) |
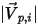 | 입자 입사 속도 크기(m/s) |
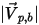 | 입자 바운스 속도 크기(m/s) |
◦ 고정 - 입자가 벽에 충돌하고 운동량과 에너지를 모두 잃으며 벽에 고정됩니다.
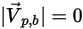
벽의 입자 누적을 고려하지 않으면 경계에 충돌한 시점에 입자가 계산에서 완전히 손실됩니다.
◦ 부분 바운스 - 완전 바운스와 고정 사이의 벽 입자 조건입니다. 입자나 흐름맥이 벽에서 바운스되지만 수직, 탄젠트 또는 수직 방향과 탄젠트 방향 모두에서 에너지의 일부가 손실됩니다. 입자의 운동량과 운동 에너지는 보존되지 않으며 입사각은 대개 반사각보다 큽니다.
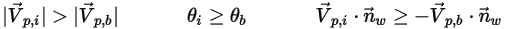
입자-벽 상호 작용을 통한 에너지 손실은 사용자 입력으로 지정됩니다.
▪ 수직 에너지 손실 - 벽에서 입자 운동 에너지의 수직 컴포넌트 손실을 지정합니다.
▪ 탄젠트 에너지 손실 - 벽에서 입자 운동 에너지의 탄젠트 컴포넌트 손실을 지정합니다.
Creo Flow Analysis에서는 최대 및 최대 수직 속도의 지정된 값에 따라 입자가 바운스되는지 아니면 고정되는지가 결정됩니다. 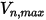 이 지정된 입자 최대 수직 속도이고
이 지정된 입자 최대 수직 속도이고 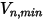 이 지정된 최소 수직 속도라고 가정하면 다음과 같은 조건이 생깁니다.
이 지정된 최소 수직 속도라고 가정하면 다음과 같은 조건이 생깁니다.
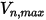 이 지정된 입자 최대 수직 속도이고
이 지정된 입자 최대 수직 속도이고 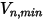 이 지정된 최소 수직 속도라고 가정하면 다음과 같은 조건이 생깁니다.
이 지정된 최소 수직 속도라고 가정하면 다음과 같은 조건이 생깁니다.▪ 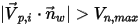 또는
또는 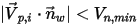 일 경우 입자가 벽에서 바운스됩니다.
일 경우 입자가 벽에서 바운스됩니다.
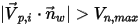 또는
또는 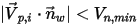 일 경우 입자가 벽에서 바운스됩니다.
일 경우 입자가 벽에서 바운스됩니다.▪ 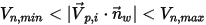 일 경우 입자가 벽에 고정됩니다.
일 경우 입자가 벽에 고정됩니다.
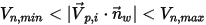 일 경우 입자가 벽에 고정됩니다.
일 경우 입자가 벽에 고정됩니다.입자-벽 상호 작용 모델은 질량 있음(Has Mass)으로 설정된 입자에만 적용됩니다. 질량 없음 입자는 벽의 흐름 유선을 따라갑니다.
입자 벽 경계는 외부 벽과 유체-솔리드 인터페이스일 수 있습니다. 개방 및 대칭 입자 경계에서와 같이, 벽 경계에서 입자가 방출될 수 있습니다.
초기 조건(입자 방출)
초기 조건은 개별 입자의 순간적인 조건을 설명하는 종속된 모든 불연속 위상 변수의 시작 값을 제공합니다. 라그랑주 시스템 입자 추적의 경우, 초기 조건을 결정하는 절차는 경계(개방, 대칭 벽, 인터페이스)에서의 입자 방출(빈도 및 분포)과 각 입자의 특성 지정으로 이루어집니다.
입자 방출(Release Particle)을 활성화할 때 다음 매개 변수나 변수가 입자 동작의 초기 조건입니다.
동작의 입자 방정식 통합
입자 동작을 추적하기 위해 라그랑주 시스템에서 각 입자의 궤적 방정식이 분석적으로 또는 숫자로 풀립니다(적분). 방정식 2.367 및 방정식 2.386에서 동작 방정식이 다음과 같이 다시 작성됩니다.
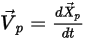
방정식 2.391
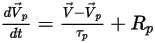
방정식 2.392
여기서 각 항목은 다음을 나타냅니다.
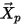 | 입자의 위치 벡터 |
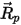 | 항력을 제외하고 중력, 회전 효과 등의 다른 모든 힘으로 인한 가속도를 포함합니다. |
방정식 2.391 및 방정식 2.392는 결합된 상미분 방정식 세트입니다. 주어진 초기 및 경계 조건이 있으면 시간 단계 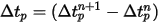 에서 입자 속도의 정방향 오일러 적분을 사용하여 입자 변위 방정식 2.391이 계산됩니다.
에서 입자 속도의 정방향 오일러 적분을 사용하여 입자 변위 방정식 2.391이 계산됩니다.
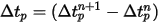 에서 입자 속도의 정방향 오일러 적분을 사용하여 입자 변위 방정식 2.391이 계산됩니다.
에서 입자 속도의 정방향 오일러 적분을 사용하여 입자 변위 방정식 2.391이 계산됩니다.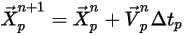
방정식 2.393
여기서 각 항목은 다음을 나타냅니다.
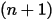 | 새 값 |
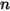 | 현재 값 |
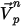 | 현재 시간 단계의 입자 속도 |
첫 번째 시간 단계에서
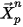 | 방출 위치 |
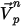 | 초기 속도 |
여기서 각 항목은 다음을 나타냅니다.

방정식 2.394
이 정방향 적분법에서는 시간 단계가 시작될 때 계산된 입자 속도가 전체 단계에 적용된다고 가정합니다. 시간 단계가 끝날 때 입자 운동량 방정식 2.392를 풀어 새 입자 속도가 계산됩니다. 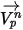 ,
, 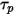 및
및 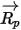 이 시간 간격
이 시간 간격 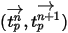 에 따라 일정하고 시간
에 따라 일정하고 시간 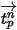 에서 시간 단계가 시작될 때 유체 특성을 가져온 경우 방정식 2.392의 분석적 해가 있다고 가정합니다.
에서 시간 단계가 시작될 때 유체 특성을 가져온 경우 방정식 2.392의 분석적 해가 있다고 가정합니다.
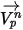 ,
, 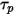 및
및 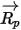 이 시간 간격
이 시간 간격 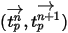 에 따라 일정하고 시간
에 따라 일정하고 시간 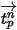 에서 시간 단계가 시작될 때 유체 특성을 가져온 경우 방정식 2.392의 분석적 해가 있다고 가정합니다.
에서 시간 단계가 시작될 때 유체 특성을 가져온 경우 방정식 2.392의 분석적 해가 있다고 가정합니다.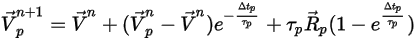
방정식 2.395
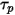 및
및 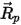 을 평가하려면 입자 위치의 밀도, 점도 및 속도와 같은 유체 변수가 필요합니다. 이들 변수는 현재 입자가 있는 유체 흐름 위상의 셀 값으로 간주됩니다. 이 분석법은 효율적이지만 시간 단계가 큰 경우 또는 입자가 연속 유체 흐름이 있는 정역학 평형 상태가 아닌 상황에서는 정확하지 않을 수 있습니다. 이런 경우 수치 체계가 방정식 2.392를 적분합니다.
을 평가하려면 입자 위치의 밀도, 점도 및 속도와 같은 유체 변수가 필요합니다. 이들 변수는 현재 입자가 있는 유체 흐름 위상의 셀 값으로 간주됩니다. 이 분석법은 효율적이지만 시간 단계가 큰 경우 또는 입자가 연속 유체 흐름이 있는 정역학 평형 상태가 아닌 상황에서는 정확하지 않을 수 있습니다. 이런 경우 수치 체계가 방정식 2.392를 적분합니다.입자-유체 결합
오일러 라그랑주 접근법에서는 연속 유체 흐름이 힘, 열, 질량 전달을 통해 입자 반응에 영향을 준다고 가정합니다. 예를 들어, 입자 힘 균형 방정식 2.370의 힘 항 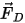 은 입자에 미치는 흐름의 공기 항력과 관련이 있습니다. 입자 위상이 불연속으로 간주되고 볼륨의 유체를 대체하지 않지만 입자는 운동량 교환을 통해(질량과 열 교환도 가능) 유체 흐름에 대응 영향력을 미칠 수 있습니다. 입자가 흐름에 미치는 영향을 입자-유체 결합이라고 합니다. 여기에는 두 범주가 있습니다.
은 입자에 미치는 흐름의 공기 항력과 관련이 있습니다. 입자 위상이 불연속으로 간주되고 볼륨의 유체를 대체하지 않지만 입자는 운동량 교환을 통해(질량과 열 교환도 가능) 유체 흐름에 대응 영향력을 미칠 수 있습니다. 입자가 흐름에 미치는 영향을 입자-유체 결합이라고 합니다. 여기에는 두 범주가 있습니다.
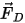 은 입자에 미치는 흐름의 공기 항력과 관련이 있습니다. 입자 위상이 불연속으로 간주되고 볼륨의 유체를 대체하지 않지만 입자는 운동량 교환을 통해(질량과 열 교환도 가능) 유체 흐름에 대응 영향력을 미칠 수 있습니다. 입자가 흐름에 미치는 영향을 입자-유체 결합이라고 합니다. 여기에는 두 범주가 있습니다.
은 입자에 미치는 흐름의 공기 항력과 관련이 있습니다. 입자 위상이 불연속으로 간주되고 볼륨의 유체를 대체하지 않지만 입자는 운동량 교환을 통해(질량과 열 교환도 가능) 유체 흐름에 대응 영향력을 미칠 수 있습니다. 입자가 흐름에 미치는 영향을 입자-유체 결합이라고 합니다. 여기에는 두 범주가 있습니다.• 단방향 결합
단방향 결합을 사용하면 유체가 입자 궤적에 영향을 줄 수 있지만 입자는 유체에 아무 영향도 미치지 않습니다. 질량 없음 입자의 경우 입자-유체 상호 작용이 단방향 결합이므로 입자가 유체 흐름을 따라 이동합니다. 질량이 있는 입자의 경우, 분산 위상 하중이 낮고 입자가 유체 흐름에 미치는 영향력이 미미한 흐름에서는 단방향 결합이 받아들일 만한 방법일 수 있습니다.
연속 유체 위상의 경우, 분산 입자 위상이 없는 단상 유체 흐름으로 흐름장이 계산됩니다. 그러면 계산된 흐름장과 초기 조건에 따라 입자 동작이 추적됩니다. 상태가 안정된 흐름의 경우, 연속성과 나비어 스톡스 방정식을 풀어 연속 위상의 수렴된 흐름 해답을 구한 후 입자 추적이 발생합니다. 과도 흐름 시뮬레이션에서 흐름 시뮬레이션의 시간 단계가 끝날 때마다 입자 동작이 추적됩니다.
• 양방향 결합
질량이 있는 입자의 경우, 양방향 결합을 사용하면 유체가 입자 궤적에 영향을 줍니다. 또한 입자가 연속 유체 위상에 영향을 줍니다. 질량 및 열 전달을 포함하지 않으면 유체와 입자의 양방향 상호 작용이 운동량 교환에만 관련이 있습니다. 연속 위상에서 불연속 위상으로 전달된 운동량은 검사 부피를 통과할 때 각각의 개별 입자가 얻거나 잃은 운동량을 추적하여 계산됩니다. 양방향 결합에서 연속체에 미치는 불연속 위상 궤적의 영향을 설명하려면 입자와 유체의 운동량 교환을 유체 운동량 방정식에 포함해야 합니다. 방정식 2.386에서 항력만 입자와 유체의 운동량 교환을 설명하며 운동량 방정식에 추가됩니다. 질량이 없는 입자의 경우 유체 흐름과 입자 간에 교환 항이 계산되지 않으므로 불연속 위상 궤적은 연속체에 아무 영향도 주지 않습니다.
연속 위상 운동량 방정식에 입자-유체 저항 효과를 포함하려면 흐름에서 이동하는 각 입자의 항력이 시간 단계 중에 입자가 있는 검사 부피에서 적용되어야 합니다. 입자 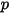 의 경우 다음 미분 방정식에서 저항
의 경우 다음 미분 방정식에서 저항 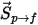 으로 인해 생기는 운동량 소스를 계산합니다.
으로 인해 생기는 운동량 소스를 계산합니다.
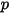 의 경우 다음 미분 방정식에서 저항
의 경우 다음 미분 방정식에서 저항 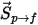 으로 인해 생기는 운동량 소스를 계산합니다.
으로 인해 생기는 운동량 소스를 계산합니다.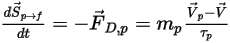
방정식 2.396
또한 연속 위상에 대한 입자 소스는 해당 입자의 숫자 유속(입자 질량으로 나눈 질량 유속)을 곱하는 소스 항 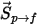 입니다.
입니다.
 입니다.
입니다.
방정식 2.397
여기서 각 항목은 다음을 나타냅니다.
 | 시간 단계 |
 | 입자 질량 유속 |
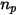 이 시간 단계
이 시간 단계 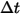 에 검사 부피를 통과하는 입자 수라고 가정할 때, 총 입자-유체 소스 항은 다음과 같습니다.
에 검사 부피를 통과하는 입자 수라고 가정할 때, 총 입자-유체 소스 항은 다음과 같습니다.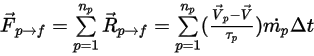
방정식 2.398
유체-입자 항력을 추가하면 연속 위상에 대해 풀이된 지배 방정식이 다음과 같이 표현됩니다.
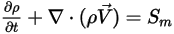
방정식 2.399
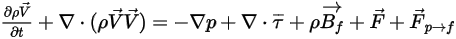
방정식 2.400
단방향 결합 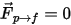 에서는 정확한 단상 연속성 및 운동량 방정식이 연속 유체 위상을 지배합니다. 양방향 결합에서는 추가 입자-유체 항력 소스 항이 생깁니다. 방정식 2.399 및 방정식 2.400은 단상 흐름과 동일하게 풀립니다.
에서는 정확한 단상 연속성 및 운동량 방정식이 연속 유체 위상을 지배합니다. 양방향 결합에서는 추가 입자-유체 항력 소스 항이 생깁니다. 방정식 2.399 및 방정식 2.400은 단상 흐름과 동일하게 풀립니다.
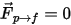 에서는 정확한 단상 연속성 및 운동량 방정식이 연속 유체 위상을 지배합니다. 양방향 결합에서는 추가 입자-유체 항력 소스 항이 생깁니다. 방정식 2.399 및 방정식 2.400은 단상 흐름과 동일하게 풀립니다.
에서는 정확한 단상 연속성 및 운동량 방정식이 연속 유체 위상을 지배합니다. 양방향 결합에서는 추가 입자-유체 항력 소스 항이 생깁니다. 방정식 2.399 및 방정식 2.400은 단상 흐름과 동일하게 풀립니다.