함수
식 편집기(Expression Editor)에서 다음 함수를 사용하면 벡터 및 스칼라를 수학적 및 논리적으로 조작할 수 있습니다.
• 연산자
◦ 벡터 및 스칼라에 공통(더하기 및 빼기 등)
◦ 스칼라에만 해당(예: 제곱근 및 로그)
◦ 벡터에만 해당(예: 내적 및 외적)
• 논리
• 삼각 및 쌍곡
• 기타 함수
• 테이블
연산자
연산자를 사용하면 벡터와 스칼라 모두를 수학적으로 조작할 수 있습니다. 다음 표에서는 a, b, c가 스칼라이고, U, V, W가 벡터입니다.
|
식 연산자
|
함수
|
예
|
|---|---|---|
|
연산자: 스칼라 및/또는 벡터
|
||
|
더하기
|
a = b+c 또는 V = U+W
|
|
|
빼기
|
a = b-c 또는 V = U-W
|
|
|
*
|
두 스칼라의 곱하기 또는 스칼라와 벡터의 곱하기
|
a = b*c 또는 V = a*U(V = U * W는 아님)
|
|
연산자: 스칼라에만 해당
|
||
|
/
|
나누기
|
a = b/c
|
|
exp(스칼라)
|
기본 e 지수 함수
|
a = exp(b)는 e를 b제곱함(a = eb)
|
|
ln(스칼라)
|
e에 대한 자연 로그 함수
|
a = ln(b)는 b의 자연 로그를 반환함
|
|
sqrt(스칼라)
|
제곱근 함수
|
a = sqrt(b)
|
|
^
|
지수 함수
|
a= b^c는 b를 c제곱함(a= bc)
|
|
연산자: 벡터에만 해당
|
||
|
&
|
벡터 내적
|
a = V&U(a = |V| |U| cos (각도))
|
|
^
|
벡터 외적
|
V=U^W (|V| = |U| |W| x sin (각도) 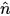 ), 오른손 법칙이 적용됩니다. ), 오른손 법칙이 적용됩니다. |
|
len(벡터)
|
벡터 V의 길이를 반환함
|
a = len(V)
|
|
normalize(벡터)
|
정규화된 단위 벡터 V/|V|를 반환함
|
V = normalize(U)
|
|
rotate(벡터, 각도, 방향, 중심)
|
회전 각도, RHR, 회전 축 및 선택적 회전 중심을 기준으로 회전된 벡터를 구합니다. 중심이 정의되지 않은 경우 기본값은 0,0,0입니다.
|
Vrot = rotate(V,알파,U,W). 여기서 V는 회전할 벡터이며, 알파는 각도(라디안 단위)이며, U는 회전 축입니다. 오른손 법칙이 적용됩니다. W는 벡터로 정의되는 선택적 중심점입니다.
|
논리
논리 함수를 사용하면 논리 문을 포함할 수 있습니다.
|
식 연산자
|
함수
|
예
|
|---|---|---|
|
true
|
논리 true
|
|
|
false
|
논리 false
|
|
|
<
|
보다 작음
|
|
|
>
|
보다 큼
|
|
|
==
|
논리 비교에서 같음
|
a = (b==3) ? 1 : 2
|
|
or
|
논리 or
|
|
|
and
|
논리 and
|
|
|
!
|
논리 부정
|
!< 보다 작지 않음
|
|
a = expression ? b : c
|
a = b(expression이 true인 경우)
a = c(expression이 false인 경우)
|
a = (b>3) ? 1 : 2 ==> (b가 3보다 큰 경우 a = 1, 그렇지 않으면 a = 2)
|
삼각 및 쌍곡
삼각 및 쌍곡 함수를 사용하면 수학 문에 해당 함수를 포함할 수 있습니다.
|
초월 식
|
함수
|
|---|---|
|
삼각
|
|
|
sin(라디안)
|
사인 함수
|
|
cos(라디안)
|
코사인 함수
|
|
cot(라디안)
|
코탄젠트 함수
|
|
tan(라디안)
|
탄젠트 함수
|
|
asin()
|
역 사인 함수, 라디안 단위로 값 반환
|
|
acos()
|
역 코사인 함수, 라디안 단위로 값 반환
|
|
acot()
|
역 코탄젠트 함수, 라디안 단위로 값 반환
|
|
atan()
|
역 탄젠트 함수, 라디안 단위로 값 반환
|
|
atan2(y,x )
|
두 개의 가변 역 탄젠트 함수(-pi, pi), 라디안 단위로 값 반환
|
|
쌍곡
|
|
|
sinh()
|
쌍곡 사인 함수
|
|
cosh()
|
쌍곡 코사인 함수
|
|
coth()
|
쌍곡 코탄젠트 함수
|
|
tanh()
|
쌍곡 탄젠트 함수
|
|
asinh()
|
역 쌍곡 사인 함수
|
|
acosh()
|
역 쌍곡 코사인 함수
|
|
acoth()
|
역 쌍곡 코탄젠트 함수
|
|
atanh()
|
역 쌍곡 탄젠트 함수
|
디스플레이 관련 함수
디스플레이 관련 함수는 디스플레이 패널을 참조합니다. 다음과 같은 작업을 수행할 수 있습니다.
• 파생된 변수의 모든 기능을 사용하여 새 변수를 작성할 수 있습니다. 피쳐에는 경계 및 아이소서피스 같은 형상 엔티티에 해당 함수를 표시하는 기능이 포함됩니다.
• 모니터 지점의 변수에 액세스
• XY 도표에 대한 사용자 변수 정의
3D 디스플레이에 대한 사용자 정의 변수
display.varname - 3D 도표에 대한 컨투어, 아이소서피스, 벡터 등의 사용자 변수를 정의합니다. 새 변수가 보기(View) 탭의 변수(Variable) 아래에 있는 특성(Properties ) 패널에 나타납니다.
#display.varname: dispname [unit] - (선택 사항) 사용자 정의 디스플레이 변수에 대한 단위를 사용하여 새 이름을 정의합니다.
예:
display.pref = flow.P - 101325
#display.pref: 게이지 압력 [Pa]
이러한 식을 사용하면 아래 그림과 같이 게이지 압력(Gauge Pressure) 엔티티가 변수(Variable) 특성 값 아래에 표시됩니다.
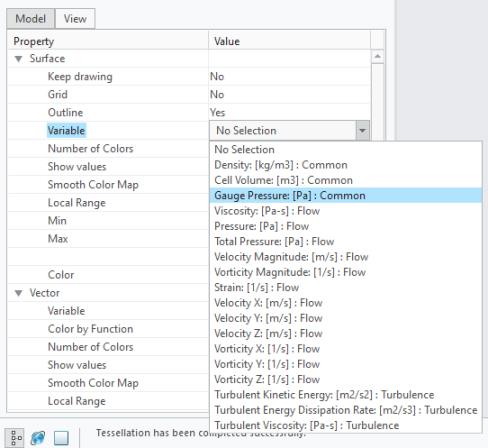
모니터 지점의 변수
다음 형식을 사용하여 모든 모니터 지점에서 로컬 셀 변수에 액세스할 수 있습니다.
module[.subname].var@probe.name
점 좌표:
probe.coord@probe_name
예:
inletP = flow.P@probe."Point01"+101325
XY 도표에 대한 사용자 정의 변수
plot.varname - XY 도표에 사용할 수 있는 사용자 변수를 정의합니다. 새 공통 변수는 특성 패널에서 변수 특성에 대한 값으로 추가됩니다.
#plot.varname: dispname [unit] - (선택 사항) 사용자 정의 변수에 대한 단위를 사용하여 새 이름을 정의합니다.
예:
plot.head = (flow.pt@outlet - flow.pt@inlet)/998/9.8
#plot.head: 압력 헤드[m]
• 새 디스플레이 또는 도표 변수 이름과 단위를 정의할 때 콜론 기호 앞에 공백을 추가하지 마십시오. • 디스플레이 및 도표 변수의 기본 단위는 대괄호 안에 표시됩니다. 예를 들어, 압력 변수에 대해 기본 단위인 Pa가 표시됩니다. 단위를 올바르게 정의하면 단위가 화면에 표시됩니다. 이 예에서 표시되는 최종 단위를 변경하면 해당 값도 변환됩니다. 단위를 올바르게 정의하지 않으면 소프트웨어에서 단위를 무시합니다. |
기타 함수
식 연산자 | 함수 | 예 |
|---|---|---|
abs(x) | 절대값 함수 | |
max(x,y) | 최대 함수 | a = max(b,c) ==> a= b(b >c인 경우) 또는 a=c(c>=b인 경우) |
min(x,y) | 최소 함수 | a = min(b,c) ==> a= b(b <c인 경우) 또는 a=c(c<=b인 경우) |
mod(x,y) | 계수 함수 | a = mod(c,b) ==> a = c를 b로 나눈 나머지 |
sgn(x) | 부호를 나타내는 플래그(-1, 0 또는 1)를 반환함 | a= sgn(b) ==> a = -1(b<0인 경우), a = 0(b=0인 경우), a = 1(b>0인 경우) |
step(x) | 계단 함수는 0에 상대적인 값에 따라 0 또는 1을 반환함 | a= step(b) ==> a = 0(b<0인 경우), a = 1(b>=0인 경우) |
테이블
table 함수를 사용하면 프로젝트 파일(*.spro)과 동일한 디렉토리에 있는 외부 테이블 파일의 데이터를 포함할 수 있습니다.
테이블 식 | 함수 |
|---|---|
table(파일 이름,x) | 1차원 테이블에서 보간 |
table(파일 이름, x, y) | 2D 테이블에서 보간 |
예:
테이블 사용:
# 테이블에서 정보 추출
p = table("inlet_pressure.txt",time)
density = table("R134a_density.txt",temp,pre)
• 테이블 형식: 1차원(파일 이름,x) - 프로젝트 파일(*.spro)과 동일한 디렉토리에 있는 1차원 데이터 테이블에 액세스할 수 있습니다.
◦ 균일 분포 형식에 대한 1차원 테이블
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="n" min="xmin" max="xmax" outside="flat | extrapolation">
# comments (x assumed to have uniform distribution)
v1
v2
...
vn
</table/>
<table size="n" min="xmin" max="xmax" outside="flat | extrapolation">
# comments (x assumed to have uniform distribution)
v1
v2
...
vn
</table/>
◦ 비균일 분포 형식에 대한 1차원 테이블
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="n" outside="flat | extrapolation">
# You can add comments by putting the hashmark “#” in front .. but do not insert comments before the xml line (line 1)
x1 v1
x2 v2
xn vn
</table/>
<table size="n" outside="flat | extrapolation">
# You can add comments by putting the hashmark “#” in front .. but do not insert comments before the xml line (line 1)
x1 v1
x2 v2
xn vn
</table/>
table 태그 아래의 outside = “flat” or outside = "extrapolation" 형식은 입력 x, y가 범위를 벗어날 때 값을 결정하는 방법을 지정합니다.
• 테이블 형식: 2D(파일 이름,x) - 프로젝트 파일(*.spro)과 동일한 디렉토리에 있는 2D 데이터 테이블에 액세스할 수 있습니다.
◦ 균일 분포에 대한 2D 테이블의 형식
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="nx my" min="xmin ymin" max="xmax ymax" outside="flat | extrapolation">
# comment
# values table (x and y assumed to have uniform distribution
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
<table size="nx my" min="xmin ymin" max="xmax ymax" outside="flat | extrapolation">
# comment
# values table (x and y assumed to have uniform distribution
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
◦ 비균일 분포에 대한 2D 테이블의 형식
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="nx my" outside ="flat | extrapolation">
# x and y variable ranges
x1 x2 … xn
y1 y2 … ym
# values table
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
<table size="nx my" outside ="flat | extrapolation">
# x and y variable ranges
x1 x2 … xn
y1 y2 … ym
# values table
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
테이블 태그 아래의 outside = “flat” or outside = "extrapolation" 형식은 입력 x, y가 범위를 벗어난 경우 값을 결정하는 방법을 지정합니다.
주석을 추가하려면 텍스트 앞에 해시 표시 "#"을 넣습니다. xml 줄 또는 줄 1 앞에는 주석을 삽입하지 마십시오. |