熱輻射の特性
熱輻射の特性は、放射オブジェクトまたはボディの以下のプロパティによって決まります。
• サーフェス温度
• サーフェスの滑らかさまたは粗さ
• スペクトル吸収率
• スペクトル放射力
電磁波として、熱輻射は周波数 (波長) のスペクトルから構成される光子エネルギーの連続的な発散に起因するものです。放射ボディでは、スペクトルの分布、波長のピーク値、および全波長の総輻射量は、放射ボディのサーフェス温度によって変化します。この結果、特定のサーフェス温度においては、放射ボディの吸収率、反射率、放射率はすべて輻射の波長によって決まります。
輻射エネルギーの交換
すべてのボディは、ランダムな方向にランダムな位相と周波数で移動する光子としてエネルギーを輻射します。あるボディのサーフェスから輻射された光子は、図 2.35 に示すように、別のボディのサーフェスに達して、吸収、反射、透過されます。輻射入射があるサーフェスの挙動は、以下の量によって記述できます。
参照: R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992
• 吸収率α - 特定の波長で吸収される入射輻射の割合。
• 反射率ρ - 特定の波長で反射される入射輻射の割合。
• 透過率τ - 特定の波長で透過する入射輻射の割合。
この 3 つの係数は輻射での電磁波の波長λの関数です。エネルギーの観点から、これらの合計が 1 にならなければなりません。
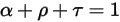
式 2.273
キルヒホッフの熱輻射の法則に従い、相反定理により、特定の波長における放射ボディの放射率はスペクトル吸収率と等しくなります。
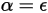
式 2.274
ここでεは放射率であり、同じ温度と波長における完全なエミッタ (黒体) からの輻射エネルギーに対する放射ボディからの輻射エネルギーの比率を表します。
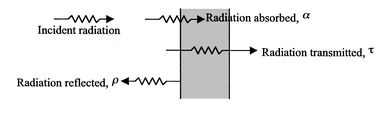
図 2.35
式 2.273 は、熱輻射に関するボディの反力は吸収率α、反射率ρ、透過率τによって特性が決まることを示しています。Α、ρ、およびτの値に応じて、以下の理想化されたタイプの放射ボディが定義されます。
R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992
• 不透過ボディ - そのボディに達した輻射をまったく透過しませんが、一部の輻射を反射できます。τ=0 およびα+ρ=1
• 透過ボディ - 達したすべての輻射を透過します。τ=1 およびα=ρ=0
• 黒体 - プランクによって提唱された理論モデル。黒体は、入射の周波数や角度に関係なく、すべての波長ですべての入射電磁輻射を吸収するオブジェクトです。輻射放射オブジェクトが熱力学的平衡における黒体の物理特性を満たす場合、その輻射は黒体輻射と呼ばれます。黒体では、α=ε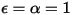
、および 
となります。
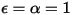、および となります。• 白体 - すべての入射光線をすべての方向に一様に完全に反射するものと見なされます。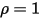
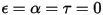
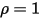および 
および 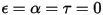• 灰色体 -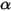 
および 
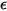が温度および波長に依存しないボディ。
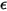はすべての波長で一様です。灰色体または灰色サーフェスからの輻射は灰色輻射と呼ばれます。灰色輻射とは異なり、波長のスペクトルがある熱輻射は非灰色輻射と呼ばれます。
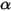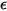および が温度および波長に依存しないボディ。 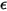はすべての波長で一様です。灰色体または灰色サーフェスからの輻射は灰色輻射と呼ばれます。灰色輻射とは異なり、波長のスペクトルがある熱輻射は非灰色輻射と呼ばれます。輻射パワー
• パワー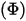 
- 特定のソースで放射、反射、透過、または受け取られる単位時間あたりの合計または正味の輻射エネルギー。
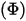- 特定のソースで放射、反射、透過、または受け取られる単位時間あたりの合計または正味の輻射エネルギー。• 放射照度 (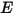
) - サーフェス 
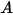が受ける単位面積あたりの輻射パワー。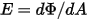
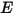) - サーフェス 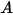が受ける単位面積あたりの輻射パワー。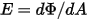• 発散度 (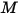
) - サーフェスから放射される単位面積あたりの輻射パワー
。
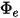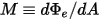
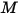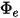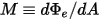
) - サーフェスから放射される単位面積あたりの輻射パワー。• 強度 (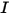
) - 特定のソースで特定の方向 (立体角、
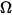) に輻射されるパワー。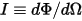
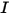) - 特定のソースで特定の方向 (立体角、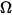) に輻射されるパワー。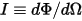• 輻射輝度 (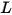
) - 特定のサーフェスによってに放射、反射、透過、または受け取られる、単位立体角あたり、単位投影面積あたりの輻射パワー。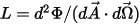
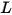) - 特定のサーフェスによってに放射、反射、透過、または受け取られる、単位立体角あたり、単位投影面積あたりの輻射パワー。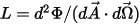• プランクの法則
任意の温度のボディによって放射される熱輻射は広範な周波数から成ります。黒体では、プランクの法則によって、黒体輻射の周波数分布はオブジェクトの温度の関数としてのみ表されます。プランクによれば、黒体のスペクトル輻射輝度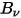 
(ボディの単位面積あたり、輻射が測定される単位立体角あたり、単位周波数 
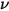あたりの放射されるパワーとして定義) にはボディ温度を基準とした公式があります。
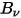(ボディの単位面積あたり、輻射が測定される単位立体角あたり、単位周波数 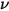あたりの放射されるパワーとして定義) にはボディ温度を基準とした公式があります。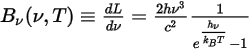
式 2.275
ここで、
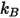 | ボルツマン定数 |
h | プランク定数 |
c | 真空または物質媒体における光速 |
スペクトル輻射輝度も単位波長λによって表されます。
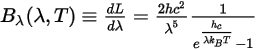
式 2.276
• シュテファン-ボルツマンの法則:
プランクの法則を周波数 v について積分した場合、シュテファン-ボルツマンの法則によって与えられるパワー出力はその温度で黒体から放射されるパワーになります。シュテファン-ボルツマンの法則は黒体輻射発散度としても知られています。シュテファン-ボルツマンの法則によれば、単位時間あたりのすべての波長における黒体の単位表面積あたりで輻射される総エネルギーは、黒体の熱力学温度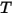 
の 4 乗に直接比例します。
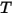の 4 乗に直接比例します。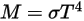
2.277
ここで、
σ | シュテファン-ボルツマン定数 |
M | 輻射発散度 |
いずれの入射輻射も吸収しない灰色体の場合、放射される総エネルギーは黒体よりも少なくなります。放射率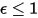 
(黒体: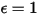 
) の導入によって、式 2.277 は灰色体では以下のように拡張されます。
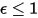(黒体: 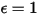) の導入によって、式 2.277 は灰色体では以下のように拡張されます。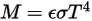
2.278
シュテファン-ボルツマンの法則から、ボディによって放射される輻射輝度とパワーは以下のように計算されます。
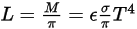
式 2.279
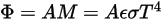
式 2.280
• ウィーンの変位則
ウィーンの変位則によれば、黒体の単位波長あたりの輻射のスペクトル輻射輝度がそのピーク値に達する波長λは温度に反比例します。
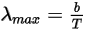
式 2.281
ここで、b はウィーンの変位定数です。
モデル定数
上記の理論モデルで使用されるモデル定数を以下の表に示します。
h | プランクの定数 | 6.626 069 3(11) ×10-34J-s = 4.135 667 43(35) ×10-15eV-s |
b | ウィーンの変位定数 | 2.897 768 5(51) ×10-3m-K |
kB | ボルツマン定数 | 1.380 650 5(24) ×10-23J/K = 8.617 343 (15) ×10-5eV/K |
σ | シュテファン-ボルツマン定数 | 5.670 373 (21) ×10-8 W/(m2-K4) |
c | 光速 | 299 792 458 m/s |