オイラーモデルと支配方程式
このセクションでは、VOF (Volume of Fluid) モデルと、混合物多相モデル、および多相流れにおける乱流と境界のモデリングに使用される支配方程式について説明します。
一般多相支配方程式
オイラー-オイラーアプローチでは、多相系内の各相 (成分) は、同じ流れ圧力を共有する数学的に相互浸透する連続体であるものとします。物理空間 (ボリューム) はすべての相によって共有されるので、相輸送を表すために相の体積分率という概念が用いられています。相の体積分率は空間と時間の連続関数であるものとし、その合計は 1 になります。各相に保存の法則が適用されて一連の支配方程式が導かれ、これらは理論的または経験的な構成関係式によって閉じられます。オイラー-オイラーアプローチには、定期的に使用される 2 つのタイプのモデルがあります。
• 不均一 (オイラー多流体) モデル - 各相 (運動量、エネルギー、乱流、種の相など) についての支配方程式と体積分率式を直接解きます。運動量、質量、種、熱の相間の相互作用と相間の移動が物理的サブモデルによってモデリングされます。
一般相スカラー ϕq (ここで q は q 番目の相を意味します) を使用した場合、相 q の一般式は以下の形式をとります。
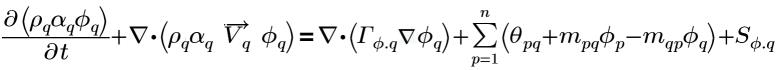
式 2.54
ここで、
ρq | q の密度 |
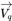 | 速度 |
Sϕq | ソース項 |
Tϕq | 拡散係数 |
αq | q 番目の相における体積分率 |
さらに、ϕq は多相系における従属変数を表します。
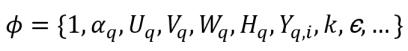
式 2.55
ここで、
Uq、Vq、Wq | 相の速度成分 |
Hq | 相の総エンタルピー |
Yqi | q 番目の相における種 "i" の質量分率 |
k | 乱流運動エネルギー |
ε | k-εモデルにおける乱流運動エネルギーの消散率 |
式 2.54 で、右辺の第 2 項は相間の交換を表しています。具体的には、
p | p 番目の相 |
n | 多相系における相の数 |
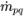 | q 番目の相から p 番目の相への質量移動 |
θpq | 運動量、エネルギー、種などの量の輸送に伴う直接の相交換 |
相間の種、質量、運動量、熱の交換を表すサブモデルを使用することで、ここで一般化されている輸送方程式から流れの支配方程式の全セットを導くことができます。
• 均一多相モデル - 不均一モデルよりも簡潔で効率のよいモデル。均一モデリングのアプローチでは、流れ、エネルギー、乱流の相支配方程式を平均化することで混合物輸送方程式のセットを導きながら、相の体積分率が計算されます。混合物スカラー ϕm では、一般支配方程式は以下の式をとります。
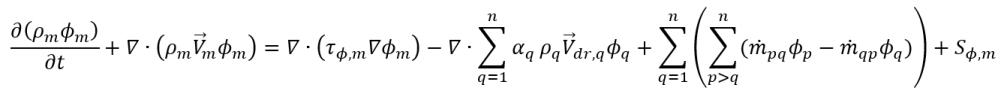
式 2.56
ここで、
m | 相の混合物 |
m が付いたすべての変数 | 相の混合物の平均値 |
さらに、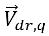
は相 q の速度と混合物速度の差です。
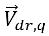は相 q の速度と混合物速度の差です。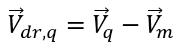
均一多相モデルは、オイラー-オイラー多相流れの相間の移動速度が高い場合に限ったケースです。すべての相が同じ圧力場を共有するという基本的仮定があります。この仮定に基づいた場合、均一モデルは、すべての相が同じ速度、温度、乱流場を共有すると見なすことによって、不均一オイラー完全多流体モデルよりも簡素化されます。これは、実装が簡単で計算効率がよいことから、オイラー完全多流体モデルの優れた代替アプローチとなります。物理的には、自由表面流れ (VOF)、キャビテーション、その他の混合度合いが高い多相流れなどの場合、運動量方程式とエネルギー方程式で相間交換モデルは不要であり、均一モデルは完全多流体モデルと同じ結果を導くことができます。
Creo Flow Analysis の現在の多相モジュールでは、均一モデリングのアプローチのみが採用されています。自由表面流れ (流体の体積モデル) と均一液体-気体 2 相流れ (混合物モデル) のモデリングに重点が置かれています。原理的には、このモデリング機能は n 相流れに適用できます。
VOF モデルと混合物多相モデル
VOF (Volume of Fluid) モデルと混合物多相モデルでは均一モデリングアプローチが使用されます。各相における体積分率の輸送方程式は式 2.54 から得られます。混合物運動量と混合物エネルギーの支配方程式は、式 2.56 および質量、運動量、エネルギーの保存の法則を使用して導かれます。このセクションでは一連の支配方程式について説明します。
• 相 q の体積分率の式
式 2.54 で、ϕq=1 を設定することで、相 q の体積分率の式が得られます。
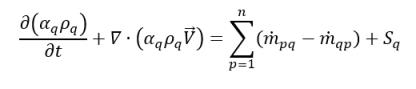
式 2.57
ここで、質量交換の項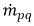 
および 
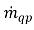は、相 q のソースとシンクをそれぞれ表しています。相間質量移動のプロセスでは、この 2 つの項のいずれかが通常はゼロになります。以下の例を参照してください。
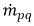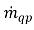および は、相 q のソースとシンクをそれぞれ表しています。相間質量移動のプロセスでは、この 2 つの項のいずれかが通常はゼロになります。以下の例を参照してください。蒸発のプロセスでは、液相 q は質量を失って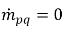 
かつ 
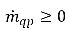となるのに対し、蒸気相では 
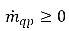かつ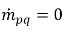 
となります。
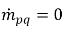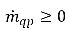かつ となるのに対し、蒸気相では 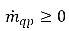かつ 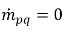となります。n 相系では、相の体積分率の合計が物理的な制約条件を満たします。
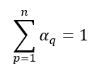
式 2.58
または、全質量保存:
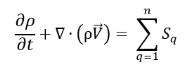
式 2.59
ここで、混合物の量は以下のように定義されます。
◦ 体積平均の混合物密度
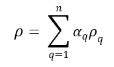
式 2.60
◦ 質量平均の混合物速度
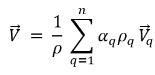
式 2.61
• 混合物の運動量方程式 - 系内にあるすべての相の個々の運動量方程式を合計することによって取得されます。式 2.56 から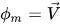 
を設定することで以下が得られます。
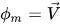を設定することで以下が得られます。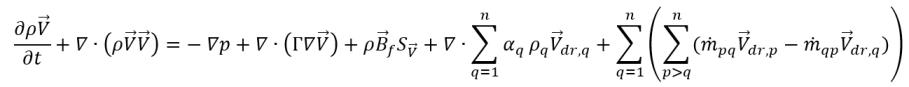
式 2.62
ここで、混合物の量は以下のように定義されます。
◦ 体積平均の混合物粘度:
式 2.63
式 2.62 における拡散係数Γは、混合物の動粘度μと乱流粘度μt を使用して計算されます。右辺の最後の 2 つの項は、直接的な運動量移動と質量移動によって誘発される運動量交換を表しています。これらは相の流動速度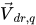 
によって決まり、以下のように定義されます。
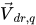によって決まり、以下のように定義されます。
式 2.69
均一アプローチでは、代数モデルを使用してこの流動速度をモデリングできます。ただし、現在の VOF モデルと混合物モデルでは、相間にすべりがないことを前提としています。
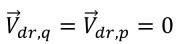
したがって、運動量交換の両方の項がゼロになります。
◦ 混合物エネルギー方程式
速度すべりがない場合、混合物でのエネルギー方程式は以下の形式をとります。
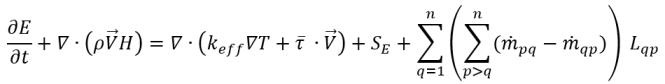
式 2.70
ここで、混合物の変数は以下のように定義されます。
▪ 体積平均の熱伝達率
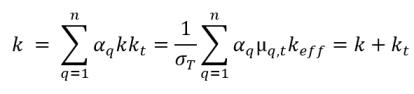
式 2.71
▪ 質量平均の混合物のエネルギーとエンタルピー
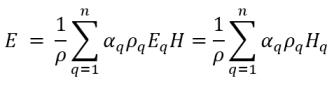
式 2.72
混合物エネルギー式 2.70 では、単相流れにおける場合と同様に粘性加熱項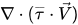 
が計算され、SE は外部熱源またはユーザー熱源の合計です。
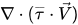が計算され、SE は外部熱源またはユーザー熱源の合計です。右辺最終項は、質量移動によって発生する界面熱伝達です。複数の相が同じ温度を共有するとした場合、Lgp は計算対象のエネルギー方程式における Hq と Hp の定義によって決まります。
熱モジュールで説明したように、物質の静的エンタルピーは、標準状態の基準エンタルピーと顕エンタルピーの 2 つの部分から成ります。相 q は流体で相 p は蒸気であるとした場合、相の静的エンタルピーの合計は以下のようになります。
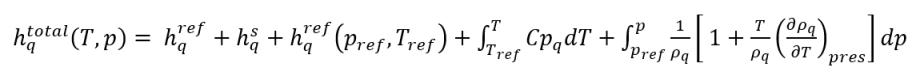
式 2.73
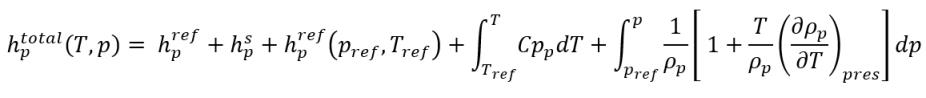
式 2.74
ここで、
pref | 参照圧力 |
Tref | 参照温度 |
hq,ref | 相 q の標準状態の基準エンタルピー |
hp,ref | 相 p の標準状態の基準エンタルピー |
基準エンタルピーの差
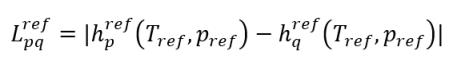
式 2.75
これは、基準温度 Tref と基準圧力 pref における潜熱です。
▪ 標準基準エンタルピーの追加:
式 2.70 で、エンタルピー H が混合物のエンタルピーの合計である場合、以下のようになります。
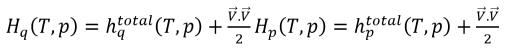
式 2.76
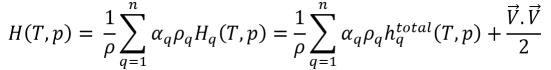
式 2.77
その場合、相形成エンタルピーによって生じる差、つまり潜熱 Lpq がエネルギー方程式にすでに含まれています。その量はゼロに設定されています。
Lpq=0
さらに、質量移動によって生じる熱伝達 (式 2.70 における右辺最終項) は、混合物エネルギー方程式ではゼロです。
▪ 標準基準エンタルピーの除外:
CFD ソルバーでは、総エンタルピーは直接解かれません。代わりに、飽和温度を基準にした顕エンタルピーだけが、計算対象のエンタルピーと内部エネルギーに含まれます。
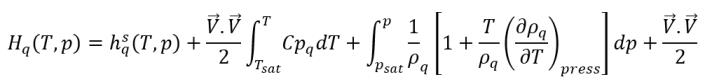
式 2.79
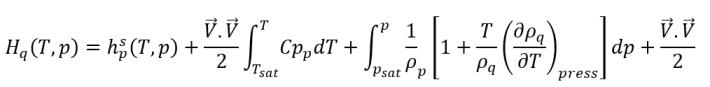
式 2.80
その場合、Lpq はゼロではありません。これは潜熱になります。
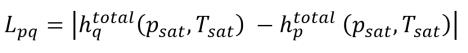
式 2.81
ここで、
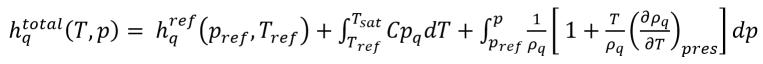
式 2.82
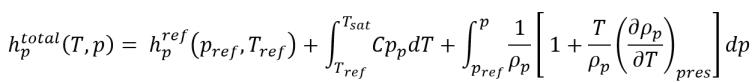
式 2.83
Creo Flow Analysis では、標準状態の基準エンタルピーがデフォルトで自動的に考慮されます。ユーザー入力は必要ありません。
乱流モデル
• 混合物 k-ε乱流モデル
VOF (Volume of Fluid) モデルと混合物多相モデルでは、単相乱流モデルの拡張を使用することによって、混相に対する乱流の影響が考慮されます。Creo Flow Analysis では、乱流モジュールで説明されている乱流モデルと壁面近傍処理が多相流れに拡張されます。混合物の流れの量では、標準モデルと RNG k-εモデルは単相乱流モデルと同じ一般式をとります。
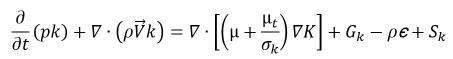
式 2.84
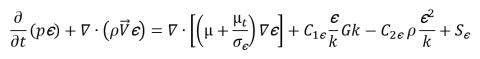
式 2.85
ここで、混合物の密度ρ、速度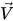 
、および分子粘度μは、それぞれ式 2.60、式 2.61、および式 2.63 内のリレーションを使用して各相の値から計算され、Sk と Sεには、可能な外部およびユーザーソースと相間相互作用のソースの両方が含まれます。混合物の乱流粘度μt は以下の式から直接計算されます。
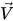、および分子粘度μは、それぞれ式 2.60、式 2.61、および式 2.63 内のリレーションを使用して各相の値から計算され、Sk と Sεには、可能な外部およびユーザーソースと相間相互作用のソースの両方が含まれます。混合物の乱流粘度μt は以下の式から直接計算されます。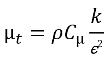
式 2.86
これに対し、乱流運動エネルギーの生成は混合物の乱流粘度と速度勾配に基づいて計算されます。
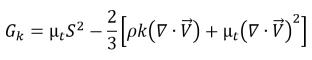
式 2.87
ここで、S は平均混合物歪み速度の率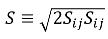 
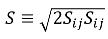です
です相 q の乱流粘度は以下のように計算できます。
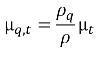
式 2.87
• 乱流拡散の影響
多相乱流の流れの場合、乱流分散力は、瞬時界面ドラッグ項を平均化すると生じ、相拡散力と同じように作用します。不均一オイラー多流体モデルは、一般的に、相の運動量方程式において、この乱流の影響を、相の体積分率の勾配によって決定される追加の相間力として扱います。ただし、この乱流の影響は、相の運動量方程式において、それを乱流拡散項として直接考慮することによってもモデリングできます。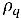
を分割し、すべてのソースを 
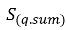(相間質量移動と外部質量ソースの合計) としてグループ化することにより、以下の支配方程式を乱流フローにおける相 q の体積分率に使用できます。
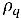を分割し、すべてのソースを 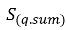(相間質量移動と外部質量ソースの合計) としてグループ化することにより、以下の支配方程式を乱流フローにおける相 q の体積分率に使用できます。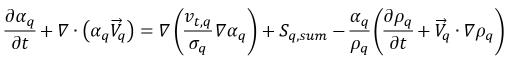
ここで、右辺の第 1 項は相 q における乱流拡散項であり、これは全質量保存を満足させるために以下の制約条件を満たす必要があります。
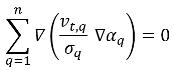
乱流拡散項は、通常、オプションとして実装されます。デフォルトでは、これは含まれていません。
多相境界のモデリング
VOF (Volume of Fluid) モデルと混合物多相モデルでは、流れおよびエネルギー方程式の境界条件は、単相流れのものと同じです。これらについては、流れおよび「熱」モジュールに説明があります。相の体積分率では、以下のように固定値とゼロ勾配のみが適用されます。
• n 相入口境界
(n-1) 相では、入口の体積分率が事前に指定されているのに対し、n 番目の相は物理的な制約条件を使用して求めます。
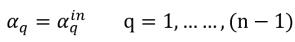
式 2.88
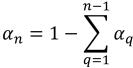
式 2.89
また、各相の体積分率が負であってはなりません。
• 出口/対称/壁面境界
(n-1) 相では、すべての出口境界、対称境界、壁面境界にゼロ勾配条件が適用されるのに対し、n 番目の相は物理的な制約条件を使用して求めます。
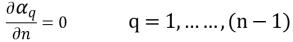
式 2.90
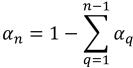
式 2.91
前述の支配方程式、乱流モデル、境界条件は、均一 VOF モデルと混合物多相モデルの基礎となります。外部またはユーザーソースの項と相間質量移動がない場合、これらは閉じた連立方程式となり、圧力に基づいた有限体積多相ソルバーを使用して数値計算されます。多くの実際の応用では、それぞれの物理的現象とプロセスを正確に取り込むには、特定のサブモデル (VOF モデルでの表面張力など) と相間質量移動が必要とされます。サブモデルを外部またはユーザーソースとしてひとまとめにするのではなく、組み込みモデルに直接含めることが推奨されます。