Casi di verifica - Analisi modali
Analisi modale di una trave a sbalzo
Enunciato del problema: si consideri una trave a sbalzo di lunghezza l, larghezza w e altezza h. Calcolare i primi 3 modi di piegatura e le frequenze naturali. Si noti che i risultati della simulazione includono i modi di piegatura ortogonale, di torsione e assiale. Il confronto dei risultati mette a confronto i primi tre modi di piegatura di una soluzione a forma chiusa con i risultati di simulazione equivalenti.
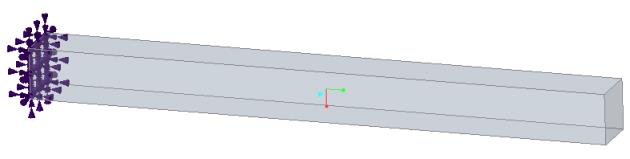
Fonte: W. T. Thompson, Theory of Vibration with Applications, 2nd Edition, Prentice-Hall, Inc., Englewood Cliffs, NJ, 1981, pag. 220
Proprietà del materiale | Proprietà geometriche |
|---|---|
Modulo di Young E = 70e9 Pa Coefficiente di Poisson ν = 0.35 Densità ⍴ = 2700 kg/m^3 | l = 4 m w = 0.346 m h = 0.346 m |
Confronto dei risultati - Dispositivo di scorrimento della qualità di simulazione nella posizione di default
Risultati | Target | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Errore percentuale |
|---|---|---|---|---|---|
Frequenza modo 1 (Hz) | 17.8 | 17.88 | 17.8 | 17.8 | 0 |
Frequenza modo 3 (Hz) | 111.5 | 110.03 | 108.3 | 108.2 | 3.05 |
Frequenza modo 6 (Hz) | 312.1 | 320.22 | 288.6 | 288.8 | 8.06 |
Confronto dei risultati per Creo Ansys Simulation (mesh di default)
Risultati | Target | Ansys AIM | Creo Ansys Simulation | Errore percentuale |
|---|---|---|---|---|
Frequenza modo 1 (Hz) | 17.8 | 17.788 | 17.76 | 0.22 |
Frequenza modo 3 (Hz) | 111.5 | 107.71 | 107.646 | 3.58 |
Frequenza modo 6 (Hz) | 312.1 | 287.07 | 287.239 | 8.79 |
Analisi modale di una trave semplice
Enunciato del problema: determinare la frequenza fondamentale di una trave semplice con una lunghezza di 80 poll e una sezione trasversale uniforme A = 4 poll2 come illustrato di seguito.

Fonte: W. T. Thompson, Vibration Theory and Applications, 2nd Printing, Prentice-Hall, Inc., Englewood Cliffs, NJ, 1965, pag. 18, es. 1.5-1
Proprietà del materiale | Proprietà geometriche |
|---|---|
Modulo di Young E = 3e7 psi Coefficiente di Poisson ν = 0.3 Densità ⍴= 0.2836 lb/poll^3 | l = 80 poll w = 2 poll h = 2 poll |
Confronto dei risultati - Dispositivo di scorrimento della qualità di simulazione nella posizione di default

Supporto semplice approssimato vincolando 0.125 in facce stampate.
Risultati | Target | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Errore percentuale |
|---|---|---|---|---|---|
Frequenza modo 1 (Hz) | 28.766 | 28.67 | 36.88 | 36.20 | 20.5 |
Confronto dei risultati per Creo Ansys Simulation (mesh di default)
Risultati | Target | Ansys AIM | Creo Ansys Simulation | Errore percentuale |
|---|---|---|---|---|
Frequenza modo 1 (Hz) | 28.766 | 28.561 | 29.4 | 2.15 |
Analisi modale di una piastra anulare
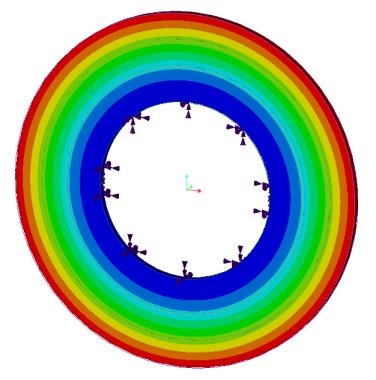
Enunciato del problema: un assieme di tre piastre anulari ha un supporto cilindrico (fissato nelle direzioni radiale, tangenziale e assiale) applicato sulla superficie cilindrica del foro. Determinare le prime sei frequenze naturali.

Fonte: R. J. Blevins, Formula for Natural Frequency and Mode Shape, Van Nostrand Reinhold Company Inc., 1979, tabella 11-2, caso 4, pag. 247
Proprietà del materiale | Proprietà geometriche |
|---|---|
Modulo di Young E = 2.9008e7 psi Coefficiente di Poisson ν = 0.3 Densità ⍴ = 0.28383 lb/poll^3 | Diametro interno della piastra interna = 20 poll Diametro interno della piastra intermedia = 28 poll Diametro interno della piastra esterna = 34 poll Diametro esterno della piastra esterna = 40 poll Spessore di tutte le piastre = 1 poll |
Confronto dei risultati - Dispositivo di scorrimento della qualità di simulazione nella posizione di default
Risultati | Target | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Errore percentuale |
|---|---|---|---|---|---|
Frequenza modo 1 (Hz) | 310.9 | 310.92 | 328.7 | 329.2 | 5.55 |
Frequenza modo 2 (Hz) | 318.1 | 316.37 | 334.6 | 335.0 | 5.04 |
Frequenza modo 3 (Hz) | 318.1 | 316.50 | 334.6 | 335.0 | 5.04 |
Frequenza modo 4 (Hz) | 351.6 | 347.80 | 366.0 | 366.8 | 4.14 |
Frequenza modo 5 (Hz) | 351.6 | 347.94 | 367.3 | 367.5 | 4.32 |
Frequenza modo 6 (Hz) | 442.4 | 436.54 | 456.4 | 456.8 | 3.15 |
Confronto dei risultati per Creo Ansys Simulation (risoluzione mesh di default)
Risultati | Target | Ansys AIM | Creo Ansys Simulation | Errore percentuale |
|---|---|---|---|---|
Frequenza modo 1 (Hz) | 310.9 | 310.16 | 312.296 | 0.45 |
Frequenza modo 2 (Hz) | 318.1 | 315.47 | 317.835 | 0.083 |
Frequenza modo 3 (Hz) | 318.1 | 315.59 | 317.847 | 0.079 |
Frequenza modo 4 (Hz) | 351.6 | 346.49 | 348.842 | 0.79 |
Frequenza modo 5 (Hz) | 351.6 | 346.52 | 349.174 | 0.69 |
Frequenza modo 6 (Hz) | 442.4 | 434.55 | 436.896 | 1.259 |
Analisi modale di una piastra rettangolare
Enunciato del problema: si consideri una piastra rettangolare con supporti fissi delle seguenti dimensioni: lunghezza = 6 poll, larghezza = 4 poll e spessore = 0.063 poll. Determinare la frequenza naturale e la forma modale.
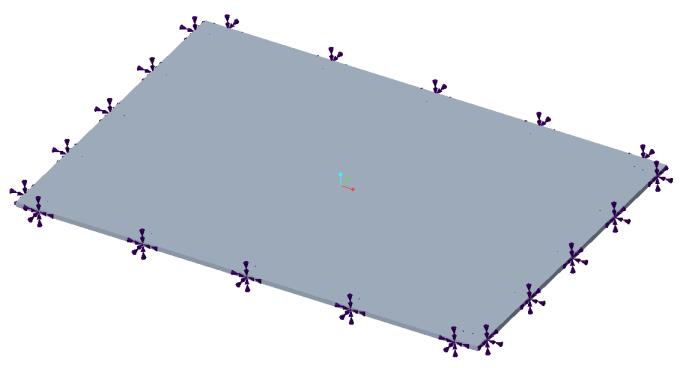
Fonte: R. Blevins, Formula for Natural Frequency and Mode Shape, Van Nostrand Reinhold Company Inc., 1979, tabella 11-6
Proprietà del materiale | Proprietà geometriche |
|---|---|
Modulo di Young E = 1.0e7 psi Coefficiente di Poisson ν = 0.33 Densità ⍴ = 0.1 lbm/poll^3 | Lunghezza = 6 poll Larghezza = 4 poll Spessore = 0.063 poll |
Confronto dei risultati - Dispositivo di scorrimento della qualità di simulazione nella posizione di default
Risultati | Target | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Errore percentuale |
|---|---|---|---|---|---|
Frequenza modo 1 (Hz) | 1016 | 1019.35 | 1123.9 | 1123 | 9.52 |
Confronto dei risultati per Creo Ansys Simulation (risoluzione mesh di default)
Risultati | Target | Ansys AIM | Creo Ansys Simulation | Errore percentuale |
|---|---|---|---|---|
Frequenza modo 1 (Hz) | 1016 | 1024.2 | 1024.79 | 0.86 |