Trasferimento di calore
Flusso laminare attraverso un tubo con potenza termica uniforme
Enunciato del problema: il flusso laminare 3D con trasferimento di calore è modellato in un tubo mediante il modulo Calore (Heat). Il fluido entra nel tubo a 300 K e viene riscaldato da una potenza termica uniforme impostata sulla parete del tubo.
à - Profilo di velocità completamente sviluppato a 300 K
Riferimenti: F.M. White, Fluid Mechanics. 3rd Edition. McGraw Hill Book Co. Inc., New York, NY, 1994.
Proprietà del fluido | Proprietà geometriche | Condizioni operative |
|---|---|---|
Densità = 13529 kg/m3 Viscosità = 0.001523 Pa-s Calore specifico = 139.3 J/kg-K Conduttività = 8.54 W/m-K | R = 0.0025 m L = 0.1 m | Entrata = Profilo di velocità completamente sviluppato a 300 K Uscita = 101325 Pa Փq = 5000 W/m2 |
Confronto dei risultati - Caduta di pressione e temperatura in uscita
Risultati | Soluzione analitica | Creo Flow Analysis | Errore percentuale |
|---|---|---|---|
Caduta di pressione (Pa) | 1 | 1.0054 | 0.54 |
Temperatura in uscita (K) | 340 | 340.894 | 0.26 |
Convezione naturale in corona circolare concentrica
Enunciato del problema: la convezione naturale è modellata in una corona circolare concentrica mediante il modulo Calore (Heat). La parete interna della corona circolare concentrica presenta una temperatura di 50 K superiore rispetto alla parete esterna.
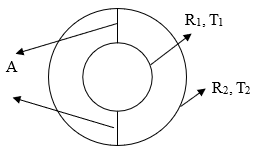
A = Piano di simmetria
Riferimenti: T.H. Kuehn, R.J. Goldstein, "An Experimental Study of Natural Convection Heat Transfer in Concentric and Eccentric Horizontal Cylindrical Annuli", Journal of Heat Transfer, Vol. 100, pp. 635-640, 1978.
Proprietà del fluido | Proprietà geometriche | Condizioni operative |
|---|---|---|
Densità = Aria o gas perfetto Viscosità = 3.54822 x 10-5 Pa-s | Profilo alare RAE 2822 Angolo di incidenza = 2.31 gradi Altezza galleria del vento = 72 m Lunghezza galleria del vento = 96 m | R1 = 0.0178 m T1 = 373 R2 = 0.04628 m T2 = 327 |
Risultato - Contorni di temperatura
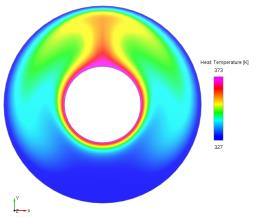
Confronto dei risultati - Distribuzione della temperatura lungo la parete di simmetria
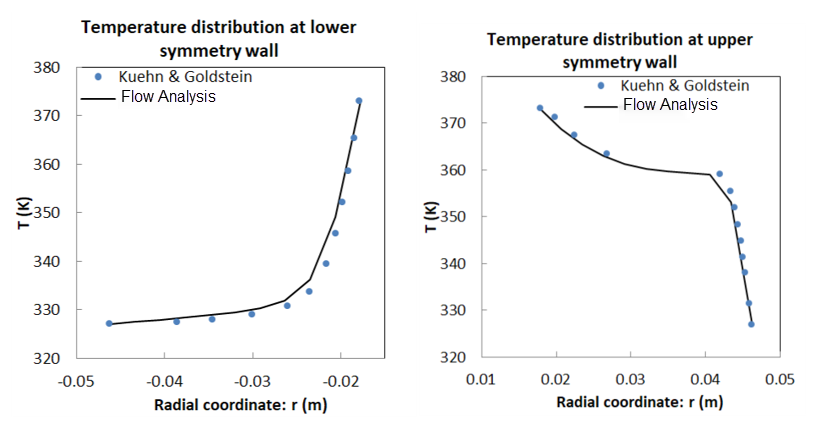
Confronto dei risultati - Confronto con dati di imaging termico

Conduzione in un blocco solido composito
Enunciato del problema: la conduzione è modellata in un blocco solido composito costituito da due materiali mediante il modulo Calore (Heat). Il sistema è riscaldato da una potenza termica impostata sulla parete destra del blocco.
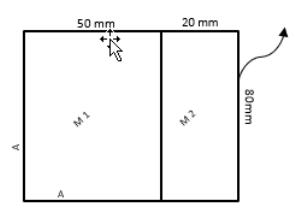
• A = Parete adiabatica
• M 1 = Materiale 1
◦ Densità = 2719 kg/m3
◦ Calore specifico = 871 J/kg-K
◦ Conduttività termica = 75 W/m-K
◦ Calore generato = 1.5*106 W/m3
• M 2 = Materiale 2
◦ Densità = 8978 kg/m3
◦ Calore specifico = 381 J/kg-K
◦ Conduttività termica = 150 W/m-K
Riferimenti: F.P. Incropera, D.P. Dewitt, Fundamentals of Heat and Mass Transfer. 5th Edition, p. 117, 2006.

Confronto dei risultati - Temperatura nel blocco composito
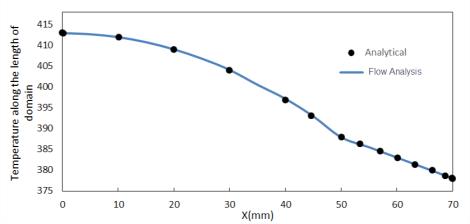
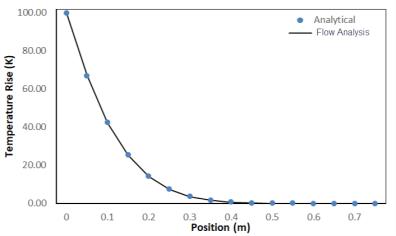
Conduzione transitoria in lastra semi-infinita
Enunciato del problema: una lastra semi-infinita viene riscaldata per 120 secondi da una potenza termica uniforme impostata sulla parete sinistra della lastra. La lastra viene misurata e le misurazioni vengono confrontate con la soluzione analitica.
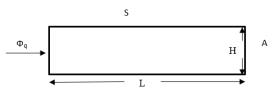
• S = Simmetria
• A = Parete adiabatica
Riferimenti: F.P. Incropera, D.P. Dewitt, T.L. Bergman, A.S. Lavine, Introduction to Heat Transfer, 5th edition, Wiley and sons, 2007.
Proprietà del solido | Proprietà geometriche | Condizioni operative |
|---|---|---|
Densità = 8995.64 kg/m3 Calore specifico = 381 J/kg-K Conduttività = 401 W/m-K | L = 0.75 m H = 0.1 m | Stato transitorio = 120 s Փq = 3 x 105 W/m2 Temperatura iniziale = 293 K |
Risultato - Contorni di temperatura

Confronto dei risultati - Aumento della temperatura lungo la lastra