Fisica
La presente sezione descrive la teoria e la modellazione nel modulo attraverso gli argomenti riportati di seguito.
Equazione di trasporto scalare
Nel modulo Specie (Species), Creo Flow Analysis risolve l'equazione di trasporto per uno scalare arbitrario definito dall'utente. Per uno scalare arbitrario,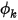 
, l'equazione di trasporto generale è nel seguente formato:
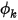, l'equazione di trasporto generale è nel seguente formato: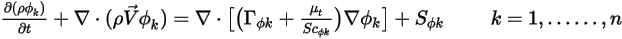
dove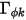 
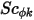e 
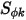sono rispettivamente i coefficienti di diffusione specificati dall'utente, il numero di Schmidt turbolento e il termine di origine per lo scalare 
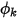. In questo caso, si presuppone che 
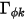sia isotropo. Può essere un valore direttamente specificato o una funzione definita dall'utente. 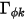viene inoltre determinato indirettamente tramite un numero di Schmidt specificato, ovvero un valore specificato o una funzione definita dall'utente. Il numero di Schmidt turbolento, 
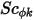, è una costante specificata dall'utente con un valore di default di uno. Il termine di origine 
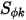può essere una costante o una funzione definita dall'utente sotto forma di origine per volume oppure origine totale nel dominio di calcolo.
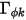
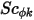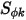e sono rispettivamente i coefficienti di diffusione specificati dall'utente, il numero di Schmidt turbolento e il termine di origine per lo scalare 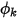. In questo caso, si presuppone che 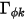sia isotropo. Può essere un valore direttamente specificato o una funzione definita dall'utente. 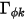viene inoltre determinato indirettamente tramite un numero di Schmidt specificato, ovvero un valore specificato o una funzione definita dall'utente. Il numero di Schmidt turbolento, 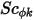, è una costante specificata dall'utente con un valore di default di uno. Il termine di origine 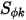può essere una costante o una funzione definita dall'utente sotto forma di origine per volume oppure origine totale nel dominio di calcolo.Selezionando il modulo Specie (Species), viene aggiunta solo un'equazione scalare. Per gli scalari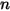 
, il modulo deve essere selezionato 
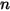volte e a ogni specie deve essere assegnato un nome diverso.
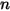, il modulo deve essere selezionato 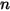volte e a ogni specie deve essere assegnato un nome diverso.L'equazione 2.376 è un'equazione scalare generale. Può essere risolta individualmente per un trasporto scalare o come aggiunta a uno o tutti i moduli standard. Poiché diffusione e termini di origine vengono determinati dagli input utente dei valori costanti o delle funzioni definite dall'utente, l'equazione di trasporto scalare generale può essere utilizzata per sviluppare nuovi modelli fisici, come i modelli di turbolenza e di combustione. Può essere utilizzata anche in forme ridotte costituite esclusivamente da alcuni termini nell'equazione. Di seguito sono indicati alcuni esempi.
• Equazione di Poisson e di Laplace
In modalità in regime stazionario, se la portata convettiva non viene risolta o rimane costante, l'equazione 2.376 viene ridotta a un problema esclusivamente di diffusione:
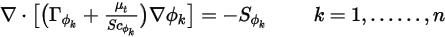
Inoltre, se la diffusione turbolenta viene ignorata (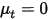
o 
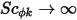) e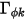 
è una costante, l'equazione 2.376 diventa un'equazione di Poisson:
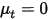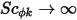o ) e 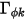è una costante, l'equazione 2.376 diventa un'equazione di Poisson: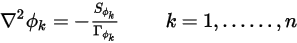
Nel caso di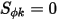 
, l'equazione 2.376 scalare viene aggiunta ulteriormente a un'equazione di Laplace.
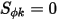, l'equazione 2.376 scalare viene aggiunta ulteriormente a un'equazione di Laplace.Tra varie applicazioni, in caso di sostituzione di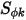 
con la densità di carica del volume (
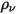) e se 
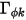è la permittività (
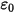), l'equazione 2.376 può essere applicata per calcolare il potenziale elettrico (
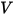) in un campo elettrico:
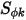con la densità di carica del volume (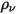) e se 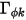è la permittività (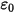), l'equazione 2.376 può essere applicata per calcolare il potenziale elettrico (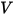) in un campo elettrico: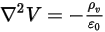
• Trasporto convettivo
Senza il termine di diffusione (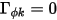
e 
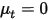o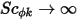 
), l'equazione 2.376 viene quindi ridotta a:
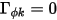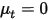e o 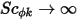), l'equazione 2.376 viene quindi ridotta a: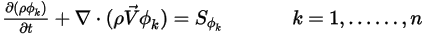
L'equazione 2.376 può essere utilizzata per modellare il trasporto delle frazioni di volume di fase (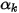
) nei flussi multifase, in cui le fasi sono immiscibili (vedere il modulo Multifase):
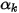) nei flussi multifase, in cui le fasi sono immiscibili (vedere il modulo Multifase):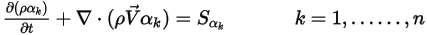
in caso di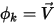 
e ⃗
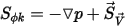, l'equazione 2.376 rappresenta le equazioni di Eulero per i flussi non viscosi:
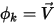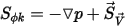e ⃗, l'equazione 2.376 rappresenta le equazioni di Eulero per i flussi non viscosi: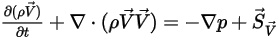
Condizioni al limite
Uno scalare definito dall'utente è una quantità fisica qualsiasi. Le condizioni al limite non vengono pertanto definite come condizioni al limite del flusso. Ad esempio, un limite di entrata del flusso può significare qualcosa di completamente diverso per lo scalare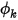 
. Di conseguenza, per l'equazione di trasporto scalare generale è possibile applicare tutti i tipi di limite definiti per i limiti fisici selezionati.
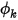. Di conseguenza, per l'equazione di trasporto scalare generale è possibile applicare tutti i tipi di limite definiti per i limiti fisici selezionati.Se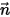 
è un vettore di unità normale alla superficie limite locale, l'espressione generale della portata per area unitaria è:
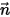è un vettore di unità normale alla superficie limite locale, l'espressione generale della portata per area unitaria è: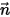se l'avvezione e la diffusione sono entrambe presenti al limite.
Per il trasporto scalare,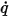 
rappresenta la portata per area unitaria che esce o entra nel dominio fisico in corrispondenza di un limite. A seconda delle applicazioni, le condizioni al limite comuni riportate di seguito derivano da questa formulazione generale.
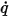rappresenta la portata per area unitaria che esce o entra nel dominio fisico in corrispondenza di un limite. A seconda delle applicazioni, le condizioni al limite comuni riportate di seguito derivano da questa formulazione generale.• Portata zero
La portata per area unitaria attraverso (normale a) il limite viene specificata su zero. Con la condizione Portata zero (Zero Flux),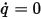 
, i flussi convettivi e diffusivi devono essere esattamente bilanciati:
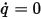, i flussi convettivi e diffusivi devono essere esattamente bilanciati: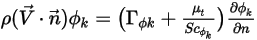
Ciò significa che se un termine è zero, anche l'altro termine deve essere zero. Ad esempio, in corrispondenza di un limite solido (parete), la velocità normale alla superficie è zero,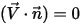 
, anche se 
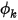può essere diverso da zero. Per soddisfare il vincolo nell'equazione 2.376, il gradiente dello scalare in corrispondenza del limite deve essere uguale a zero, 
.
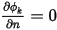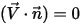, anche se 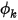può essere diverso da zero. Per soddisfare il vincolo nell'equazione 2.376, il gradiente dello scalare in corrispondenza del limite deve essere uguale a zero, 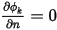.In Creo Flow Analysis, in corrispondenza di una parete, Portata zero (Zero Flux) è la condizione al limite di default per lo scalare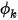 
.
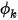.• Valore specificato
Valore specificato (Specified Value) è una condizione al limite in cui il valore dello scalare al limite,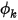 
, viene determinato direttamente da un valore di input utente di 
:
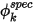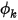, viene determinato direttamente da un valore di input utente di :
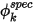In Creo Flow Analysis, in corrispondenza di un'entrata di flusso, Valore specificato (Specified Value) è la condizione al limite di default per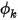 
.
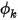.• Simmetria
Per una condizione al limite Simmetria (Symmetry) viene applicato il gradiente zero normale al limite per lo scalare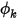 
:
:
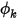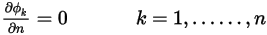
In Creo Flow Analysis, in corrispondenza di un limite di simmetria di flusso, anche Simmetria (Symmetry) è la condizione al limite di default per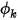 
.
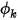.• Uscita
Uscita (Outlet) viene utilizzato come condizione al limite in corrispondenza dell'apertura da cui il flusso deve uscire o entrare nel dominio. Per un'uscita di pressione specificata (resistenza o condensatore nel flusso), si tratta della condizione di default per lo scalare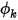 
.
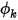.In corrispondenza di un limite di uscita, l'input richiesto è il valore specificato per lo scalare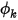 
. La condizione al limite effettiva applicata per 
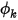dipende dalle condizioni di flusso:
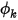. La condizione al limite effettiva applicata per 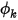dipende dalle condizioni di flusso:◦ Flusso in uscita dal dominio - Se il flusso esce dal dominio di calcolo da un'uscita o in corrispondenza di un'entrata tramite flusso inverso, viene presupposto il gradiente zero in corrispondenza del limite:
◦ Flusso in entrata nel dominio - Se il flusso entra nel dominio di calcolo da un'entrata o in corrispondenza di un'uscita tramite flusso inverso, si applica il valore specificato per il limite:
• Portata convettiva
In corrispondenza di un limite, la portata convettiva di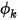 
per area unitaria (
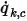) viene determinata come funzione del valore di ambiente esterno dello scalare (
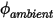) e di un coefficiente di scambio (
):
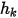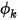per area unitaria (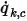) viene determinata come funzione del valore di ambiente esterno dello scalare (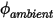) e di un coefficiente di scambio ():
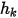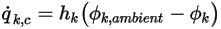
dov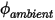e 
e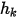 
sono parametri di input utente. Il coefficiente di scambio 
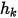ha l'unità di 
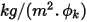. Dalla portata convettiva nota 
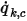, il valore del limite di 
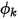viene ottenuto dall'equazione 2.376.
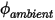e 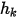sono parametri di input utente. Il coefficiente di scambio 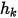ha l'unità di 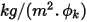. Dalla portata convettiva nota 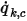, il valore del limite di 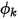viene ottenuto dall'equazione 2.376.• Portata scalare specificata
In questa condizione al limite, la portata dello scalare viene specificata nei due modi descritti di seguito.
◦ Portata per area - Nell'equazione 2.376, la portata scalare per area unitaria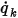 
viene specificata da un input utente come valore costante o funzione definita dall'utente:
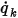viene specificata da un input utente come valore costante o funzione definita dall'utente:
Dall'equazione 2.376 si ottiene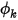 
in base alle condizioni di flusso.
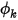in base alle condizioni di flusso.◦ Portata totale - La portata scalare totale è nota tramite un input utente come valore costante o funzione definita dall'utente:
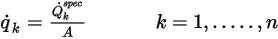
dove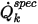 
è la portata scalare totale specificata e 
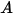è l'area del limite totale. Si ottiene quindi 
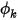dall'equazione 2.376 in base alle condizioni di flusso.
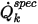è la portata scalare totale specificata e 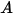è l'area del limite totale. Si ottiene quindi 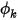dall'equazione 2.376 in base alle condizioni di flusso.