Modellazione dell'erosione delle particelle
L'erosione è un fenomeno che causa la perdita di materiale per l'impatto ripetuto di particelle solide su una superficie. L'erosione danneggia tubi, valvole e altri canali di passaggio del flusso. È quindi importante studiare il tasso di erosione e identificare le aree suscettibili a questo fenomeno nei canali di passaggio del flusso.
La modellazione dell'erosione basata su CFA include i passi descritti di seguito.
1. I dati del campo di flusso, ad esempio la velocità, vengono ottenuti risolvendo le equazioni di Navier-Stokes.
2. Le particelle vengono rilasciate all'interno del campo di flusso e monitorate singolarmente per ottenere informazioni quali la velocità di impatto e l'angolo di impatto.
3. Le informazioni sull'impatto delle particelle vengono utilizzate in un'equazione di erosione per calcolare il rapporto/tasso di erosione o la perdita di massa di superficie causata dall'impatto delle particelle.
Le equazioni di erosione studiano gli effetti di vari parametri sull'erosione, tra cui i paramenti descritti di seguito.
Riferimenti: Mazdak Parsi et al. "A comprehensive review of solid particle erosion modeling for oil and gas wells and pipelines applications" (2014)
• Caratteristiche delle particelle, ad esempio dimensione, forma, densità, durezza e così via.
• Informazioni sull'impatto delle particelle, ad esempio velocità di impatto delle particelle 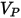 , angolo di impatto
, angolo di impatto 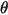 , interazione particella-particella e così via.
, interazione particella-particella e così via.
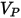 , angolo di impatto
, angolo di impatto 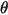 , interazione particella-particella e così via.
, interazione particella-particella e così via.• Proprietà della parete su cui impattano le particelle, ad esempio densità del materiale, durezza e così via.
Le equazioni di erosione calcolano il tasso di erosione 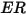 , definito come la quantità di perdita di materiale della parete (dovuta all'impatto di particelle solide) divisa per la massa delle particelle solide impattanti.
, definito come la quantità di perdita di materiale della parete (dovuta all'impatto di particelle solide) divisa per la massa delle particelle solide impattanti.
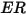 , definito come la quantità di perdita di materiale della parete (dovuta all'impatto di particelle solide) divisa per la massa delle particelle solide impattanti.
, definito come la quantità di perdita di materiale della parete (dovuta all'impatto di particelle solide) divisa per la massa delle particelle solide impattanti.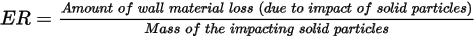
Creo Flow Analysis utilizza i modelli di erosione descritti dettagliatamente nelle sezioni indicate di seguito.
Riferimenti: Mazdak Parsi etc. "CFD simulation of sand particle erosion in gas-dominant multiphase flow" (2015)
Modello di Finne
L'equazione di erosione di Finne si esprime come:
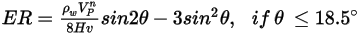
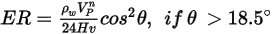
dove
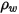 | densità del materiale della parete (kg/m3) |
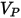 | velocità di impatto della particella (m/s) |
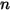 | esponente di velocità (uguale a 2 nella maggior parte delle applicazioni industriali) |
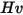 | durezza di Vicker (Pa) |
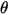 | angolo di impatto (grado) |
Questo modello sottovaluta l'asportazione di materiale per gli angoli di impatto delle particelle maggiori di 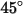 e non considera alcuna erosione per gli impatti normali. e non considera alcuna erosione per gli impatti normali. |
Modello di Zhang
L'equazione di erosione di Zhang si esprime come:
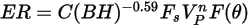
dove
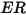 | tasso di erosione |
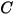 | 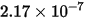 |
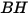 | durezza di Brinell del materiale della parete (Pa) |
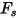 | fattore di forma della particella |
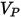 | velocità di impatto della particella (m/s) |
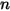 | esponente della velocità (uguale a 2.41) |
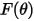 | funzione dell'angolo di impatto |
Il fattore di forma della particella 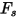 presenta i valori riportati di seguito per tipi diversi di particelle di sabbia.
presenta i valori riportati di seguito per tipi diversi di particelle di sabbia.
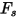 presenta i valori riportati di seguito per tipi diversi di particelle di sabbia.
presenta i valori riportati di seguito per tipi diversi di particelle di sabbia.Valore | Tipo di particella di sabbia |
|---|---|
1.0 | tagliente o angolare |
0.53 | semiarrotondato |
0.2 | completamente arrotondato |
La funzione dell'angolo di impatto si esprime nel modo seguente:
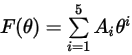
Nella tabella riportata di seguito sono elencati i valori di 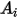 .
.
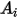 .
.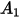 | 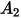 | 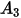 | 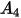 | 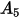 |
|---|---|---|---|---|
5.40 | -10.11 | 10.93 | -6.33 | 1.42 |
Modello di Oka
L'equazione di erosione di Oka et al. si presenta nel seguente modo:
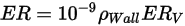
Equazione 2.406
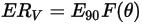
Equazione 2.407
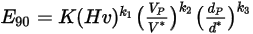
Equazione 2.408
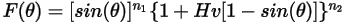
Equazione 2.409
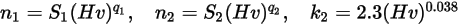
Equazione 2.410
dove
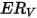 | tasso di erosione volumetrica (mm3/kg) |
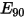 | danni da erosione a un angolo di impatto normale (mm3/kg) |
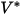 | velocità di impatto di riferimento (m/s) |
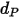 | diametro della particella (m) |
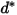 | diametro della particella di riferimento (m) |
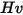 | durezza di Vicker (GPa) |
I valori dei diversi coefficienti utilizzati nell'equazione 2.406, nell'equazione 2.407, nell'equazione 2.408, nell'equazione 2.409 e nell'equazione 2.410 sono indicati nella seguente tabella:
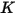 | 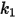 | 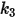 | 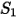 | 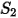 | 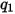 | 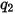 |
|---|---|---|---|---|---|---|
60 | -0.12 | 0.19 | 0.71 | 2.4 | 0.14 | -0.94 |
Modello di DNV
L'equazione di erosione di DNV si esprime come segue:
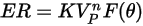
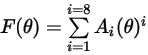
dove
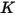 | 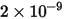 |
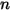 (esponente di velocità) (esponente di velocità) | 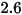 |
Nella tabella riportata di seguito sono elencati i valori di 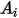 .
.
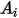 .
.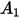 | 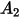 | 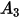 | 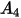 | 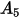 |  | 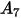 | 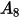 |
|---|---|---|---|---|---|---|---|
9.370 | -42.295 | 110.864 | -175.804 | 170.137 | -98.398 | 31.211 | -4.170 |
Modello di Mansouri
L'equazione di erosione di Mansouri si esprime come segue:
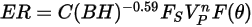
Equazione 2.413
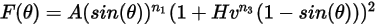
Equazione 2.414
dove
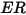 | tasso di erosione |
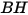 | durezza di Brinell del materiale della parete (Pa) |
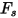 | fattore di forma della particella |
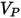 | velocità di impatto della particella (m/s) |
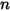 | esponente di velocità |
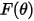 | funzione dell'angolo di impatto |
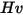 | durezza di Vicker (Pa) |
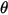 | angolo di impatto (grado) |
La tabella riportata di seguito contiene i valori dei diversi parametri utilizzati nell'equazione 2.413 e nell'equazione 2.414 dell'equazione di erosione di Mansouri (2015).
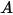 | 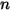 | 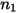 | 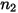 | 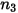 | 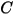 |
|---|---|---|---|---|---|
0.6947 | 2.41 | 0.2 | 0.85 | 0.65 | 4.49 e-07 |
Modello di Grant-Tabakoff
L'equazione di erosione del modello Grant-Tabakoff si esprime come segue:
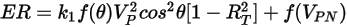
Equazione 2.415
dove
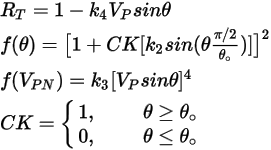
Equazione 2.416
dove
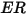 | tasso di erosione |
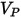 | velocità di impatto della particella (m/s) |
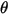 | angolo di impatto (grado) |
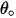 | angolo di erosione massima (grado) |
Il tasso di erosione 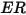 nell'equazione 2.415 è definito come la quantità, in milligrammi, di materiale rimosso per unità di massa (grammo) di particelle impattanti. L'unità di velocità è ft/s.
nell'equazione 2.415 è definito come la quantità, in milligrammi, di materiale rimosso per unità di massa (grammo) di particelle impattanti. L'unità di velocità è ft/s.
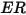 nell'equazione 2.415 è definito come la quantità, in milligrammi, di materiale rimosso per unità di massa (grammo) di particelle impattanti. L'unità di velocità è ft/s.
nell'equazione 2.415 è definito come la quantità, in milligrammi, di materiale rimosso per unità di massa (grammo) di particelle impattanti. L'unità di velocità è ft/s.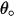 è l'angolo di erosione massima, ad esempio
è l'angolo di erosione massima, ad esempio 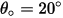 per una lega basata su alluminio.
per una lega basata su alluminio.I valori dei diversi coefficienti per il modello Grant-Tabakoff sono indicati nella tabella riportata di seguito.
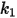 | 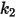 | 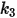 | 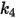 |
3.67 e-06 | 0.585 | 6e-12 | 0.0016 |