Wärmeübertragung
Laminare Strömung in einem Rohr mit gleichmäßigem Wärmestrom
Problemstellung: Eine laminare 3D-Strömung mit Wärmeübertragung in einem Rohr wird mit dem Modul "Heat" modelliert. Flüssigkeit tritt mit 300 K in das Rohr ein und wird durch einen gleichmäßigen Wärmestrom an der Wand des Rohrs erwärmt.
à – voll entwickeltes Geschwindigkeitsprofil bei 300 K
Referenzen: F.M. White. Fluid Mechanics. 3rd Edition. McGraw Hill Book Co. Inc., New York, NY, 1994.
Flüssigkeitseigenschaften | Geometrische Eigenschaften | Arbeitsbedingungen |
|---|---|---|
Dichte = 13529 kg/m3 Viskosität = 0.001523 Pa-s Spezifische Wärme = 139.3 J/kg-K Leitfähigkeit = 8.54 W/m-K | R = 0.0025 m L = 0.1 m | Einlass – voll entwickeltes Geschwindigkeitsprofil bei 300 K Austritt = 101325 Pa Փq = 5000 W/m2 |
Ergebnisvergleich – Druckabfall und Austrittstemperatur
Ergebnisse | Analytische Lösung | Creo Flow Analysis | Prozentualer Fehler |
|---|---|---|---|
Druckabfall (Pa) | 1 | 1.0054 | 0.54 |
Austrittstemperatur (K) | 340 | 340.894 | 0.26 |
Natürliche Konvektion in einem konzentrischen Kreisring
Problemstellung: Die natürliche Konvektion in einem konzentrischen Kreisring wird mit dem Modul "Heat" modelliert. Die Innenwand des konzentrischen Kreisrings ist 50 K wärmer als die Außenwand.
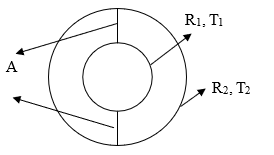
A = Symmetrieebene
Referenzen: T.H. Kuehn, R.J. Goldstein, "An Experimental Study of Natural Convection Heat Transfer in Concentric and Eccentric Horizontal Cylindrical Annuli", Journal of Heat Transfer, Vol 100, S. 635-640, 1978.
Flüssigkeitseigenschaften | Geometrische Eigenschaften | Arbeitsbedingungen |
|---|---|---|
Dichte = Allgemeine Gas- oder Luftgleichung Viskosität = 3.54822 x 10-5 Pa-s | Tragflächenprofil RAE2822 Anstellwinkel = 2.31 Grad Windkanalhöhe = 72 m Windkanallänge = 96 m | R1 = 0.0178 m T1 = 373 R2 = 0.04628 m T2 = 327 |
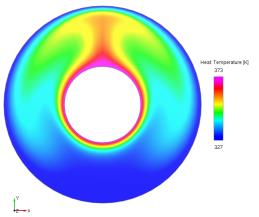
Ergebnis – Temperaturkonturen
Ergebnisvergleich – Temperaturverteilung entlang Symmetriewand
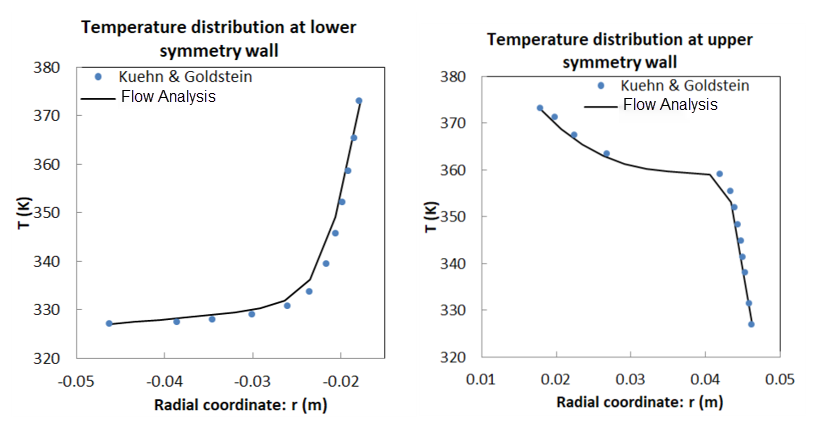
Ergebnisvergleich – Vergleich mit Wärmebilddaten

Wärmeleitung in einem zusammengesetzten, massiven Block
Problemstellung: Die Wärmeleitung in einem zusammengesetzten, aus zwei Materialen bestehenden massiven Block wird mit dem Modul "Heat" modelliert. Ein Wärmestrom an der rechten Wand des Blocks erwärmt das System.
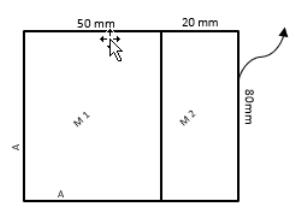
• A = adiabatische Wand
• M 1 = Material 1
◦ Dichte = 2719 kg/m3
◦ Spezifische Wärme = 871 J/kg-K
◦ Wärmeleitfähigkeit = 75 W/m-K
◦ Erzeugte Wärme = 1.5*106W/m3
• M 2 = Material 2
◦ Dichte = 8978 kg/m3
◦ Spezifische Wärme = 381 J/kg-K
◦ Wärmeleitfähigkeit = 150 W/m-K
Referenzen: F.P. Incropera, D.P. Dewitt.Fundamentals of Heat and Mass Transfer. 5th Edition, S. 117, 2006.

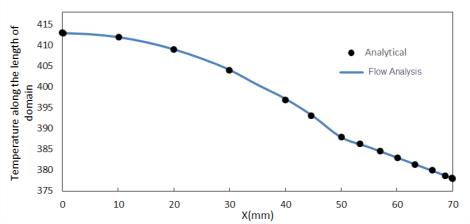
Ergebnisvergleich – Temperatur im zusammengesetzten Block
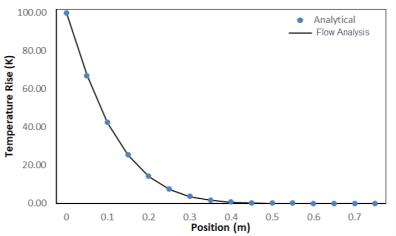
Transiente Wärmeleitung in einer halbunendlichen Platte
Problemstellung: Eine halbunendliche Platte wird für 120 Sekunden durch einen gleichmäßigen Wärmestrom an der linken Wand der Platte erwärmt. Die Platte wird gemessen, und die Messungen werden mit der analytischen Lösung verglichen.
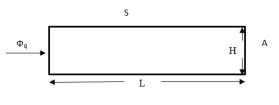
• S = Symmetrie
• A = adiabatische Wand
References: F.P. Incropera, D.P. Dewitt, T.L. Bergman, A.S. Lavine, Introduction to Heat Transfer, 5th edition, Wiley and sons, 2007.
Volumenkörpereigenschaften | Geometrische Eigenschaften | Arbeitsbedingungen |
|---|---|---|
Dichte = 8995.64 kg/m3 Spezifische Wärme = 381 J/kg-K Leitfähigkeit = 401 W/m-K | L = 0.75 m H = 0.1 m | Transient = 120 s Փq = 3 x 105 W/m2 Anfangstemperatur = 293 K |
Ergebnis – Temperaturkonturen

Ergebnisvergleich – Temperaturanstieg in der Platte