Physik
In diesem Abschnitt werden die Theorie und Modellierung im Modul anhand der folgenden Themen beschrieben:
Skalar-Transportgleichung
Im Modul Spezies (Species) löst Creo Flow Analysis die Transportgleichung für einen beliebigen, benutzerdefinierten Skalar. Für einen beliebigen Skalar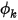 
hat die allgemeine Transportgleichung die folgende Form:
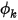hat die allgemeine Transportgleichung die folgende Form: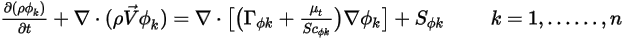
Dabei sind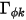 
, 
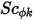und 
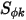der vom Benutzer festgelegte Diffusionskoeffizient, die Schmidt-Zahl (Gas) und der Quellausdruck für den Skalar 
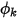. Hier wird angenommen, dass 
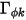isotrop ist. Dies kann ein direkt angegebener Wert oder eine benutzerdefinierte Funktion sein. 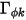wird auch indirekt durch eine angegebene Schmidt-Zahl bestimmt, die ein angegebener Wert oder eine benutzerdefinierte Funktion ist. Die Schmidt-Zahl (Gas) 
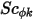ist eine vom Benutzer angegebene Konstante und hat einen Standardwert von 1. Der Quellausdruck 
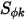kann eine Konstante oder eine benutzerdefinierte Funktion in Form einer Quelle pro Volumen oder die Gesamtquelle in der Berechnungsdomäne sein.
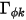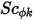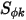, und der vom Benutzer festgelegte Diffusionskoeffizient, die Schmidt-Zahl (Gas) und der Quellausdruck für den Skalar 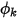. Hier wird angenommen, dass 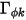isotrop ist. Dies kann ein direkt angegebener Wert oder eine benutzerdefinierte Funktion sein. 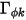wird auch indirekt durch eine angegebene Schmidt-Zahl bestimmt, die ein angegebener Wert oder eine benutzerdefinierte Funktion ist. Die Schmidt-Zahl (Gas) 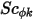ist eine vom Benutzer angegebene Konstante und hat einen Standardwert von 1. Der Quellausdruck 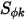kann eine Konstante oder eine benutzerdefinierte Funktion in Form einer Quelle pro Volumen oder die Gesamtquelle in der Berechnungsdomäne sein.Beachten Sie, dass durch Auswahl des Moduls "Spezies" nur eine Skalar-Gleichung hinzugefügt wird. Für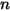 
-Skalare muss das Modul 
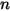-mal ausgewählt werden, und jeder Spezies wird ein anderer Name zugewiesen.
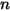-Skalare muss das Modul 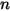-mal ausgewählt werden, und jeder Spezies wird ein anderer Name zugewiesen.Gleichung 2.376 ist eine allgemeine Skalar-Gleichung. Sie kann einzeln für einen Skalar-Transport oder als Ergänzung zu einem oder allen Standardmodulen gelöst werden. Da die Diffusions- und Quellausdrücke durch Benutzereingaben von Konstantenwerten oder benutzerdefinierten Funktionen bestimmt werden, kann die allgemeine Skalar-Transportgleichung verwendet werden, um neue physikalische Modelle wie Turbulenz- und Verbrennungsmodelle zu entwickeln. Sie kann auch in reduzierten Formen verwendet werden, die nur aus einigen Ausdrücken in der Gleichung bestehen. Die Beispiele sind unten angegeben:
• Poisson- und Laplace-Gleichung
Wenn der konvektive Strom im stationären Modus nicht gelöst wird oder konstant bleibt, wird Gleichung 2.376 auf ein reines Diffusionsproblem reduziert:
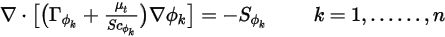
Wenn die Wirbeldiffusion ignoriert wird (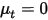
oder 
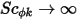) und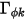 
eine Konstante ist, wird Gleichung 2.376 ferner zu einer Poisson-Gleichung:
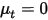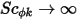oder ) und 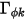eine Konstante ist, wird Gleichung 2.376 ferner zu einer Poisson-Gleichung: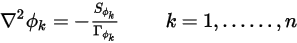
Wenn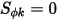 
, dann hat die Gleichung 2.376 des Skalars zusätzlich zu einer Laplace-Gleichung beigetragen.
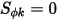, dann hat die Gleichung 2.376 des Skalars zusätzlich zu einer Laplace-Gleichung beigetragen.Wenn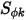 
durch die Volumenladungsdichte (
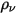) ersetzt wird und 
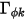die Permittivität ist (
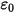), kann Gleichung 2.376 bei vielen Anwendungen eingesetzt werden, um das elektrische Potential (
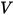) in einem elektrischen Feld zu berechnen:
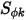durch die Volumenladungsdichte (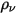) ersetzt wird und 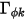die Permittivität ist (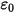), kann Gleichung 2.376 bei vielen Anwendungen eingesetzt werden, um das elektrische Potential (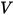) in einem elektrischen Feld zu berechnen: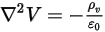
• Konvektiver Transport
Ohne den Diffusionsausdruck (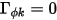
und 
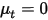oder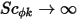 
) wird Gleichung 2.376 dann reduziert auf:
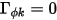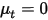und oder 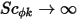) wird Gleichung 2.376 dann reduziert auf: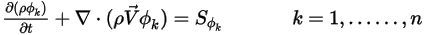
Gleichung 2.376 kann zum Modellieren des Transports der Phasenvolumenbrüche (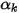
) in Mehrphasenströmen verwendet werden, in denen die Phasen nicht mischbar sind (siehe Modul Multiphase):
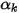) in Mehrphasenströmen verwendet werden, in denen die Phasen nicht mischbar sind (siehe Modul Multiphase):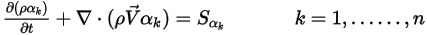
wenn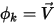 
und ⃗
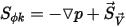, dann repräsentiert Gleichung 2.376 die Euler-Gleichungen für nicht viskose Flüsse:
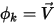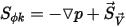und ⃗, dann repräsentiert Gleichung 2.376 die Euler-Gleichungen für nicht viskose Flüsse: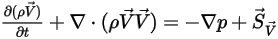
Randbedingungen
Ein benutzerdefinierter Skalar ist eine beliebige physikalische Größe. Die Randbedingungen sind daher nicht als Flussrandbedingungen definiert. Beispielsweise kann eine Fluss-Einlassberandung für den Skalar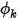 
durchaus etwas anderes bedeuten. Anschließend können Sie für die allgemeine Skalar-Transportgleichung alle definierten Berandungstypen für die von Ihnen ausgewählten physikalischen Berandungen anwenden.
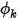durchaus etwas anderes bedeuten. Anschließend können Sie für die allgemeine Skalar-Transportgleichung alle definierten Berandungstypen für die von Ihnen ausgewählten physikalischen Berandungen anwenden.Wenn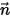 
ein Einheitenvektor senkrecht zur lokalen Berandungsfläche ist, ist der allgemeine Ausdruck des Massenstroms pro Flächeneinheit:
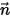ein Einheitenvektor senkrecht zur lokalen Berandungsfläche ist, ist der allgemeine Ausdruck des Massenstroms pro Flächeneinheit: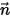wenn Advektion und Diffusion an der Berandung vorhanden sind.
Für den Skalar-Transport stellt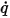 
den Strom pro Flächeneinheit dar, der die physische Domäne an einer Berandung verlässt oder in diese gelangt. Je nach Anwendung werden die folgenden allgemeinen Randbedingungen von dieser allgemeinen Formulierung abgeleitet:
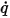den Strom pro Flächeneinheit dar, der die physische Domäne an einer Berandung verlässt oder in diese gelangt. Je nach Anwendung werden die folgenden allgemeinen Randbedingungen von dieser allgemeinen Formulierung abgeleitet:• Nullstrom
Strom pro Flächeneinheit über die Berandung hinweg (senkrecht zur Berandung) wird auf 0 festgelegt. Mit der Bedingung des Nullstroms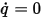 
müssen die konvektiven und diffusen Ströme genau ausgeglichen sein:
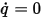müssen die konvektiven und diffusen Ströme genau ausgeglichen sein: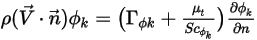
Dies bedeutet Folgendes: Wenn ein Ausdruck 0 ist, muss der andere Ausdruck auch 0 sein. Beispielsweise ist bei einer Volumenkörperberandung (Lasche) die senkrechte Geschwindigkeit zur Fläche 0,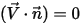 
, obwohl 
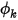evtl. nicht 0 ist. Der Gradient des Skalars an der Berandung muss 0 sein, 
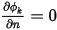, um die Randbedingung in Gleichung 2.376 zu erfüllen.
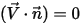, obwohl 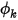evtl. nicht 0 ist. Der Gradient des Skalars an der Berandung muss 0 sein, 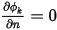, um die Randbedingung in Gleichung 2.376 zu erfüllen.In Creo Flow Analysis an einer Lasche ist der Nullstrom die Standardrandbedingung für den Skalar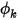 
.
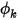.• Angegebener Wert
"Angegebener Wert" (Specified Value) ist eine Randbedingung, unter der der Wert des Skalars an der Randbedingung,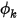 
, direkt von einem Benutzereingabewert von 
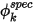bestimmt wird:
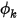, direkt von einem Benutzereingabewert von 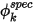bestimmt wird:
In Creo Flow Analysis an einem Flusseinlass ist der angegebene Konstantenwert die Standardrandbedingung für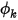 
.
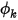.• Symmetrie
Für eine Symmetrie-Randbedingung wird der Senkrecht-zu-Berandung-Gradient 0 für den Skalar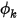 
angewendet:
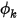angewendet: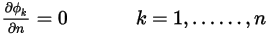
In Creo Flow Analysis bei einer Fluss-Symmetrie-Berandung ist die Symmetrie auch die Standard-Randbedingung für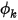 
.
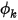.• Auslass
"Auslass" (Outlet) ist eine Randbedingung an einer Öffnung, an der der Fluss die Domäne voraussichtlich verlässt oder in sie gelangt. Für einen angegeben Druckabfluss oder einen Widerstand oder Kondensator im Fluss ist dies die Standardbedingung für den Skalar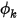 
.
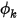.An einer Auslassberandung ist die erforderliche Eingabe der angegebene Wert für Skalar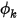 
. Die tatsächliche Randbedingung, die für 
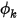angewendet wird, hängt von den Flussbedingungen ab:
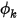. Die tatsächliche Randbedingung, die für 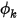angewendet wird, hängt von den Flussbedingungen ab:◦ Fluss aus der Domäne – Wenn der Fluss die Berechnungsdomäne aus einem Auslass oder an einem Einlass durch einen umgekehrten Fluss verlässt, wird ein Gradient 0 an der Berandung angenommen:
◦ Fluss in die Domäne – Wenn der Fluss in die Berechnungsdomäne aus einem Einlass oder an einem Auslass durch einen umgekehrten Fluss gelangt, gilt der angegebene Wert für die Berandung:
• Konvektiver Strom
An einer Berandung wird der konvektive Strom von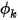 
pro Flächeneinheit (
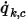) als Funktion des externen Umgebungswerts des Skalars (
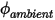) und eines Austauschkoeffizienten (
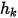) bestimmt:
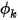pro Flächeneinheit (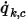) als Funktion des externen Umgebungswerts des Skalars (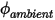) und eines Austauschkoeffizienten (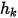) bestimmt: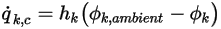
wobei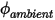 
und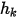 
Benutzereingabeparameter sind. Beachten Sie, dass der Austauschkoeffizient 
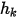die Einheit 
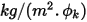aufweist. Aus dem bekannten konvektiven Strom 
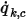wird der Berandungswert 
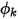aus Gleichung 2.376 abgeleitet.
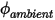und 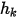Benutzereingabeparameter sind. Beachten Sie, dass der Austauschkoeffizient 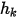die Einheit 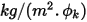aufweist. Aus dem bekannten konvektiven Strom 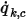wird der Berandungswert 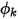aus Gleichung 2.376 abgeleitet.• Specified Scalar Flux
In dieser Randbedingung wird der Strom des Skalars auf zwei Arten angegeben:
◦ Strom pro Fläche – In Gleichung 2.376 wird der Skalar-Strom pro Flächeneinheit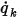 
von einer Benutzereingabe als Konstantenwert oder benutzerdefinierte Funktion angegeben:
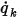von einer Benutzereingabe als Konstantenwert oder benutzerdefinierte Funktion angegeben:
Dann wird aus Gleichung 2.376 basierend auf den Flussbedingungen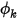 
abgeleitet.
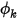abgeleitet.◦ Gesamtstrom (Total Flux) - Der gesamte Skalarstrom ist durch eine Benutzereingabe als Konstantenwert oder benutzerdefinierte Funktion bekannt:
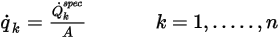
wo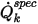 
der angegebene gesamte Skalarstrom und 
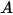die gesamte Berandungsfläche ist. 
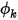wird aus Gleichung 2.376 basierend auf den Flussbedingungen abgeleitet.
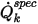der angegebene gesamte Skalarstrom und 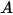die gesamte Berandungsfläche ist. 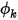wird aus Gleichung 2.376 basierend auf den Flussbedingungen abgeleitet.