Allgemeine Einführung: Biegetabellen
Biegetabellen steuern die Biegeaufmaßberechnungen der entwickelten Länge für flaches Material, das für eine Biegung in einer Geometrie mit Bögen benötigt wird. Die entwickelte Länge hängt vom Materialtyp, seiner Dicke und den Biegeradien ab. Sie können eine beliebige Anzahl Biegetabellen in ein Teil kopieren; einem Teil kann aber jeweils nur eine Biegetabelle zugewiesen sein. Alle KEs, die der zugewiesenen Biegetabelle zugeordnet sind, werden bei der Regenerierung aktualisiert. Sie können auch ein KE-spezifisches Biegeaufmaß erzeugen, indem Sie während der Laschenerzeugung eine andere Biegetabelle zuweisen.
|
|
Für Biegungen mit unterschiedlichen Radien, wie Kegel oder Zylinder, verwenden Sie Y-Faktor oder K-Faktor, um die entwickelte Länge zu berechnen.
|
Es gibt drei Standardbiegetabellen für die 90°-Biegungen, die im Machinery's Handbook, 28. Auflage, enthalten sind:
|
Tabelle
|
Material
|
Y-Faktor
|
K-Faktor
|
|---|---|---|---|
|
Tabelle 1
|
Weichmessing und -kupfer
|
0.55
|
0.35
|
|
Tabelle 2
|
Hartmessing und -kupfer, Flussstahl, Aluminium
|
0.64
|
0.41
|
|
Tabelle 3
|
Hartkupfer, Bronze, kaltgewalzter Stahl, Federstahl
|
0.71
|
0.45
|
Sie können auch benutzerdefinierte Biegetabellen für die Unterstützung zusätzlicher Materialtypen sowie Methoden zur Berechnung der entwickelten Länge definieren. Wenn Sie eine eigene Biegetabellen-Bibliothek erstellen, legen Sie den Dateipfad anhand der Konfigurationsoption pro_sheet_met_dir <vollständiger Verzeichnispfad> fest. Die folgenden Informationen sind in einer Biegetabelle enthalten:
• Formel (Formula) – Verwaltet die Werte für das Biegeaufmaß oder die Entwicklungslänge mit Berechnungen und Logikanweisungen. Die Formel L = (Π/2 x R + Y-Faktor x T) Θ/90 wird nur für Radius- und Dickewerte verwendet, die sich außerhalb des Bereichs der Tabellendaten befinden.
• Tabellendaten (Table Data) – Listet Radius- und Blechdickenwerte mit dem entsprechenden Biegeaufmaß bzw. der entwickelten Länge auf. Eine Biegetabelle muss mindestens eine Spalte und eine Zeile mit tabulierten Daten enthalten. Biegeaufmaßdaten müssen nicht in jede Tabellenzelle eingegeben werden. Alle nicht in der Tabelle gefundenen Werte werden interpoliert. Wenn Sie nur die Biegetabellenformeln anwenden möchten, schließen Sie Daten ein, die nicht in der Konstruktion verwendet werden (Radius = 1000, Dicke = 1000). Geben Sie für 90°-Biegungen immer Tabellendaten an. Für andere Biegungen als 90° Biegungen werden die Werte mit Θ/90 multipliziert, wobei Θ der spezifische Biegewinkel in Grad ist.
• Materialdaten (Materials Data) – Listet die Materialien auf, auf die die Biegetabelle angewendet werden kann. Sie erhalten eine Warnung, wenn der Materialtyp eines Bauteils nicht in der Liste enthalten ist. Die von Ihnen verwendeten Materialien müssen zwischen STARTMATERIAL und ENDMATERIAL aufgelistet sein. Material wird in der ersten Spalte in Großbuchstaben eingegeben (ein Material pro Zeile).
|
|
In der Materialdatenliste muss die Groß-/Kleinschreibung beachtet werden. Stellen Sie sicher, dass der Materialtyp des Teils einem Typ in der Materialdatenliste entspricht.
|
• Konvertierungsgleichung (Conversion Equation) – Verwendet die Biegeaufmaßwerte aus der Biegetabelle, um die entwickelte Länge zu berechnen. So führt z.B. die Gleichung L = 2 * (T + R)-A Anpassungen an den Werten für das Biegeaufmaß durch, wie im nachfolgenden Beispiel gezeigt. Wenn sich die angegebenen Werte für Dicke und Biegeradius innerhalb des Bereichs der Tabellendaten befinden, jedoch nicht in der Tabelle angezeigt werden, wird das entsprechende Biegeaufmaß durch Interpolation der Werte für das Biegeaufmaß der Tabelle berechnet. In der unten erläuterten Interpolationsmethode zur Berechnung des Biegeaufmaßes wird dies verdeutlicht. Wird keine Konvertierungsgleichung angegeben, dann ist die entwickelte Länge gleich dem Biegeaufmaß. Befinden sich die Radius- und Dickewerte außerhalb des Bereichs der Tabellendaten, dann wird die Biegetabelle ignoriert und die von Creo Parametric definierte Formel verwendet.
Das folgende Beispiel zeigt eine Gleichung für spezifische Biegewinkelbereiche:
Wenn WINKEL (ANGLE) > 0 oder WINKEL (ANGLE) < = 90 wird ein bekannter Parameter zur Berechnung der entwickelten Länge verwendet.
SFLAT = X + Y - A
Bekannt:
X = T + R + b
SFLAT = a + b + L
Durch Ersetzung:
a + b + L = (T + R + a) — A
ODER
Die Konvertierungsgleichung:
L = 2 * (T + R) — A
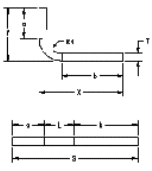
Dabei gilt:
T = Dicke
A = Biegewinkel
R = Biegeradius
A = Biegeaufmaß
SFLAT = X + Y - A, wobei SFLAT die gesamte Abisolierlänge ist.
Die bekannten Parameter, die zur Berechnung der entwickelten Länge verwendet werden, lauten:
X = T + R +b
Y = T + R + a
SFLAT = a + b + L
Durch Ersetzung:
a + b + L = (T + R + b) + (T + R + a) - A
ODER
L = 2 * (T + R)-A – die Gleichung zur KONVERTIERUNG.
Das folgende Programm zeigt z.B., wie eine Formel und eine Konvertierungsgleichung zur Interpolation verwendet werden.
FORMULA
IF R<=2
IF ANGLE > 0 & ANGLE < 90
L = (ANGLE * PI/180) * (R + T/2)
L = (ANGLE * PI/180) * (R + T/2)
ENDIF
IF ANGLE >= 90 & ANGLE < 180
L = (ANGLE * PI/180) * (R + T/3)
ENDIF
ENDIF
IF R>2
L = (ANGLE * PI/180) * (R)
ENDIF
END FORMULA
!
CONVERSION
IF ANGLE > 0 & ANGLE <=90
L = 2 * (T + R) - 0,4285 * A
ELSE
L = 2 * (T + R) - .3567917 * A
ENDIF
END CONVERSION
Im Anschluss folgt die Gleichung für die Interpolationsmethode, die zur Berechnung des Biegeaufmaßes verwendet wird.
A1,1*(Ty-T0)*(RY-R0) + A0,1*(T1-Ty)*(Ry-R0) + A1,0*(TY-T0)*(R1-RY) + A0,0*(T1-TY)*(R1-RY)
Ay = --------------------------------------------------------------------------------------------------
(T1-T0)*(R1-R0)
Dabei gilt:
A0,0 ist das Aufmaß für T0,R0
A1,0 ist das Aufmaß für T1,R0
A0,1 ist das Aufmaß für T0,R1
A1,1 ist das Aufmaß für T1,R1
Im Beispiel oben gilt: T0 < Ty < T1 und R0 < Ry < R1.
Bei T0 = T1 = Ty können Sie die folgende Formel verwenden:
A1,1 (Ry-R0) + A1,0 (R1-Ry)
Ay = -----------------------------
(R1 - R0)
Im Beispiel oben gilt: A1,0 = A0,0 und A1,1 = A0,1.
Bei R0 = R1 = Ry können Sie die folgende Formel verwenden:
A1,1 (Ty -T0) + A0,1 (T1-Ty)
Ay = ------------------------------
(T1 -T0)
Im Beispiel oben gilt: A0,0 = A1,1 = A1,0
Dabei gilt:
T = Dicke
R = Radius