辐射熱傳建模
在熱流體系統中,固體表面和/或流體流可能會因為輻射而被加熱或冷卻。在 CFA 模型中,將透過求解辐射傳輸方程式 (RTE) 並求出總能量守恆方程式的辐射源項來解釋辐射熱傳。Creo Flow Analysis 中所選的模型,即表面對表面 (S2S) 輻射模型,是一種廣泛使用的建模方法。
辐射傳輸方程式
當輻射光線以特定方向穿過吸收、發射與散射介質層時,輻射光線會因為背離輻射光線方向的吸收與散射現象而失去能量。輻射光線還會透過在朝向輻射光線方向的發射與散射現象,從介質中的光源獲得能量。若光線在介質無限層上的總能量平衡,即會得到一個微分方程式,稱為辐射傳輸方程式 (RTE)。
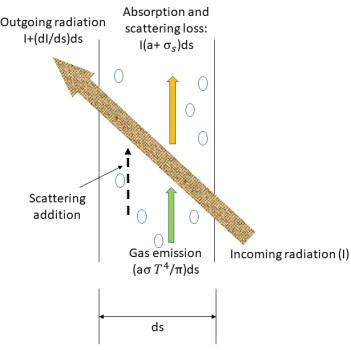
為了導出辐射傳輸方程式,可以考慮強度為 I 的入射輻射光線穿過一介質 (例如氣體),在 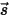 方向上的增量厚度為 ds,如圖所示。位置
方向上的增量厚度為 ds,如圖所示。位置 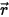 ⃗ 處和方向
⃗ 處和方向 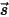 上的入射光線會透過介質層以四種方式發生改變,其作用在於增強 (能量獲得 +) 或減弱 (能量損失) 輻射強度
上的入射光線會透過介質層以四種方式發生改變,其作用在於增強 (能量獲得 +) 或減弱 (能量損失) 輻射強度 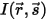 :
:
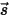 方向上的增量厚度為 ds,如圖所示。位置
方向上的增量厚度為 ds,如圖所示。位置 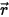 ⃗ 處和方向
⃗ 處和方向 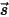 上的入射光線會透過介質層以四種方式發生改變,其作用在於增強 (能量獲得 +) 或減弱 (能量損失) 輻射強度
上的入射光線會透過介質層以四種方式發生改變,其作用在於增強 (能量獲得 +) 或減弱 (能量損失) 輻射強度 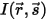 :
:• 吸收 - 介質 (例如氣體) 會吸收穿過其中的一小部份輻射能量。若吸收係數為 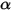 ,則透過吸收而損失的輻射能量為:
,則透過吸收而損失的輻射能量為:
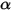 ,則透過吸收而損失的輻射能量為:
,則透過吸收而損失的輻射能量為: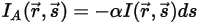
方程式 2.282
• 散射 - 當光線穿過介質 (例如氣體) 時,介質會散射一小部份輻射能量到另一方向 (背離方向 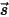 )。若散射係數為
)。若散射係數為 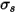 ,則透過散射而損失的輻射能量為:
,則透過散射而損失的輻射能量為:
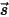 )。若散射係數為
)。若散射係數為 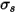 ,則透過散射而損失的輻射能量為:
,則透過散射而損失的輻射能量為: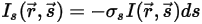
方程式 2.283
• 發射 - 介質會作為灰體,根據其局部溫度 (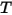 ) 與光線的發射特性來發射光線之輻射能量。根據斯特凡-波茲曼定律及發射與吸收之間的互易性 (方程式 2.274 與方程式 2.279),由介質發射出的輻射率為:
) 與光線的發射特性來發射光線之輻射能量。根據斯特凡-波茲曼定律及發射與吸收之間的互易性 (方程式 2.274 與方程式 2.279),由介質發射出的輻射率為: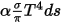
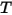 ) 與光線的發射特性來發射光線之輻射能量。根據斯特凡-波茲曼定律及發射與吸收之間的互易性 (方程式 2.274 與方程式 2.279),由介質發射出的輻射率為:
) 與光線的發射特性來發射光線之輻射能量。根據斯特凡-波茲曼定律及發射與吸收之間的互易性 (方程式 2.274 與方程式 2.279),由介質發射出的輻射率為: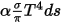
此外,假設 n 為介質的折射率 (定義為光在真空中行進之速度與其在指定介質中行進之速度的比值),則透過輻射光線獲得的實際能量為:
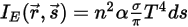
方程式 2.284
• 其他輻射源的散射 - 介質層中其他輻射源的一小部份會被散射為輻射光線,需端視位置和方向向量 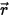 與
與 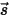 而定。引入
而定。引入 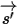
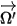 來表示輻射束的方向和立體角,以及
來表示輻射束的方向和立體角,以及 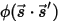 來表示相位函數之後,在各個方向上傳播之光線散射到
來表示相位函數之後,在各個方向上傳播之光線散射到 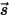 ⃗方向的強度分量如下:
⃗方向的強度分量如下:
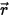 與
與 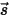 而定。引入
而定。引入 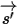
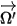 來表示輻射束的方向和立體角,以及
來表示輻射束的方向和立體角,以及 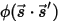 來表示相位函數之後,在各個方向上傳播之光線散射到
來表示相位函數之後,在各個方向上傳播之光線散射到 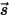 ⃗方向的強度分量如下:
⃗方向的強度分量如下: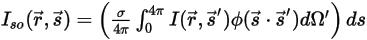
方程式 2.285
請注意,在方程式 2.285 中,略過了散射過程。
若入射輻射能量為 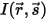 ,出射輻射能量為
,出射輻射能量為 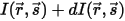 ,則方向
,則方向 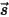 ⃗ 上的辐射能量平衡具有如下形式:
⃗ 上的辐射能量平衡具有如下形式:
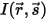 ,出射輻射能量為
,出射輻射能量為 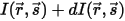 ,則方向
,則方向 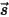 ⃗ 上的辐射能量平衡具有如下形式:
⃗ 上的辐射能量平衡具有如下形式: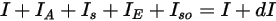
方程式 2.286
將方程式 2.282 至方程式 2.285 代入方程式 2.286,然後除以 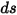 ,即得到如下所示的辐射傳輸方程式 (RTE):
,即得到如下所示的辐射傳輸方程式 (RTE):
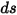 ,即得到如下所示的辐射傳輸方程式 (RTE):
,即得到如下所示的辐射傳輸方程式 (RTE):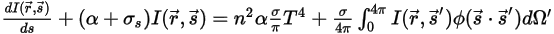
方程式 2.287
RTE 是固定方向 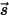 上輻射強度
上輻射強度 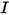 的一階積分微分方程式。若要在某一域內求解此方程式,需要給出此域內的溫度場,還需要給出內部與外部表面上
的一階積分微分方程式。若要在某一域內求解此方程式,需要給出此域內的溫度場,還需要給出內部與外部表面上 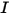 的邊界條件,以及兩種不同介質之間的介面。
的邊界條件,以及兩種不同介質之間的介面。
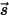 上輻射強度
上輻射強度 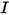 的一階積分微分方程式。若要在某一域內求解此方程式,需要給出此域內的溫度場,還需要給出內部與外部表面上
的一階積分微分方程式。若要在某一域內求解此方程式,需要給出此域內的溫度場,還需要給出內部與外部表面上 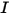 的邊界條件,以及兩種不同介質之間的介面。
的邊界條件,以及兩種不同介質之間的介面。局部介質溫度是透過求解總能量 (包括輻射源) 守恆方程式得到的,如熱模組中所述。但是,對於熱輻射,邊界處理較為複雜,且需端視輻射模型而定。一般而言,邊界可以是發射、反射與吸收能量的不透明介質,也可以是能夠透射能量的半透明介質。反射與透射可以是漫射和/或鏡面反射。例如,在灰體輻射的發射與反射不透明邊界上,根據反射類型,光線強度可以表示如下:
◦ 存在漫辐射與反射的不透明邊界:
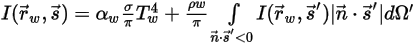
方程式 2.288
◦ 存在漫輻射與鏡面反射的不透明邊界:
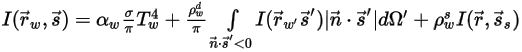
方程式 2.289
其中,
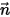 ⃗ ⃗ | 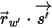 位置處法向於表面的單位向量 位置處法向於表面的單位向量 |
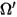 | 漫反射光線之方向與立體角 (在各個方向上均勻反射) |
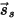 | 鏡面反射光線之方向 (根據入射角實現完美反射) |
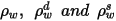 | 表面反射度、漫反射度以及鏡面反射度,分別具有下列關係: 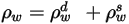 方程式 2.290 |
在指定的邊界條件下,方程式 2.287 用於控制指定方向上輻射強度的傳輸。對於灰體輻射,應在球面內的各個不同方向上求解方程式 2.287。對於非灰體輻射,其強度還與波長相關。因此,需要在整個波段範圍內的各個方向上進行求解。很顯然,直接求解辐射傳輸方程式會非常耗時。因此,在許多工程模擬中,最好使用已進行一定簡化處理但比較接近的模型來解釋方向與光譜相依性。在 CFD 模擬中,通常會採用下列輻射模型,詳細描述可在下列參照中找到。
參考資料:R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Rosseland 輻射模型
參考資料:R, Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ P-1 輻射模型
參考資料:R. Siegel and J. R. Howell, Thermal Radiation Heat Transfer, Hemisphere Publishing Corporation, Washington DC, 1992.
▪ 離散傳輸輻射模型
參照:N. G. Shah, A New Method of Computation of Radiant Heat Transfer in Combustion Chambers”, PhD thesis, Imperial College of Science and Technology, London, England, 1979.
參考資料:M. G. Carvalho, T. Farias, and P. Fontes, "Predicting Radiative Heat Transfer in Absorbing, Emitting, and Scattering Media Using the Discrete Transfer Method", In W. A. Fiveland et al., editor, Fundamentals of Radiation Heat Transfer, volume 160, pages 17-26.ASME HTD, 1991.
▪ 表面對表面 (S2S) 輻射模型
參考資料:R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ 離散座標 (DO) 輻射模型
參考資料:G. D. Raithby and E. H. Chui, "A Finite-Volume Method for Predicting a Radiant Heat Transfer in Enclosures with Participating Media", J. Heat Transfer, 112:415-423, 1990.
參考資料:E. H. Chui and G. D. Raithby, "Computation of Radiant Heat Transfer on a Non-Orthogonal Mesh Using the Finite-Volume Method", Numerical Heat Transfer, Part B, 23:269-288, 1993.
每個模型在精度與成本方面都有其自身的優點和限制。例如,雖然 Rosseland 模型無法求解入射輻射的傳輸方程式,但它是運作速度最快的輻射模型,並且需要的額外記憶體最少。由於 Rosseland 的辐射傳輸方程式過度簡化,因此,該模型僅能用於具有光學厚度 (光學厚度為介質中入射輻射功率與透射輻射功率之比值的自然對數) 的介質。
離散座標 (DO) 輻射模型會將方程式 2.287 轉換為以空間座標 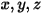 表示的輻射強度傳輸方程式,並針對與向量方向
表示的輻射強度傳輸方程式,並針對與向量方向 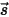 相關聯的有限個離散立體角進行求解。所選立體角的數量直接決定了精度與計算成本。DO 建模方法也與用於流體流動與能量方程式的方法相同。目前,該模型是涵蓋整個光學厚度範圍的最為一般的輻射模型,適合解決從表面對表面輻射到參與輻射 (例如燃燒系統) 等問題。但是,DO 模型針對非灰體輻射的計算成本很高。
相關聯的有限個離散立體角進行求解。所選立體角的數量直接決定了精度與計算成本。DO 建模方法也與用於流體流動與能量方程式的方法相同。目前,該模型是涵蓋整個光學厚度範圍的最為一般的輻射模型,適合解決從表面對表面輻射到參與輻射 (例如燃燒系統) 等問題。但是,DO 模型針對非灰體輻射的計算成本很高。
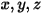 表示的輻射強度傳輸方程式,並針對與向量方向
表示的輻射強度傳輸方程式,並針對與向量方向 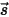 相關聯的有限個離散立體角進行求解。所選立體角的數量直接決定了精度與計算成本。DO 建模方法也與用於流體流動與能量方程式的方法相同。目前,該模型是涵蓋整個光學厚度範圍的最為一般的輻射模型,適合解決從表面對表面輻射到參與輻射 (例如燃燒系統) 等問題。但是,DO 模型針對非灰體輻射的計算成本很高。
相關聯的有限個離散立體角進行求解。所選立體角的數量直接決定了精度與計算成本。DO 建模方法也與用於流體流動與能量方程式的方法相同。目前,該模型是涵蓋整個光學厚度範圍的最為一般的輻射模型,適合解決從表面對表面輻射到參與輻射 (例如燃燒系統) 等問題。但是,DO 模型針對非灰體輻射的計算成本很高。在上述輻射模型中,表面對表面 (S2S) 輻射模型特別適合對封閉體辐射傳輸進行建模,而不需考量參與介質。典型範例有辐射空間加熱器,以及汽車發動機罩和車身底部系統。在這些情況下,參與輻射的輻射模型有時不奏效。儘管視因子計算本身可以是 CPU 密集型,但相較於 DO 輻射模型,S2S 模型每次迭代所需的時間更短、執行速度更快。在 Creo Flow Analysis 中,目前選擇的辐射熱傳模型是 S2S 輻射模型。
表面對表面 (S2S) 輻射模型
表面對表面輻射模型解釋了在沒有參與介質的情況下灰體漫射表面所構成之封閉體中的輻射交換。表面對表面辐射能量交換取決於兩個主要因素:所牽涉表面的辐射特徵,以及幾何參數,後者包括表面積與形狀,及與其他位置之間的相對位置 (分隔距離與方位)。在 S2S 輻射模型中,表面辐射熱傳被視為灰體漫射輻射模型,而幾何參數由名為視因子的幾何函數予以解釋。
• 灰體漫射輻射
S2S 輻射模型假設表面為灰體,且具有漫射特性 (灰體輻射)。對於灰體表面,表面的發射率 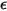 與吸收率
與吸收率 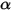 二者皆與出射光線與入射光線的波長無關。根據 Kirchhoff 熱輻射定律 (如方程式 2.274 所表示),發射率等於吸收率:
二者皆與出射光線與入射光線的波長無關。根據 Kirchhoff 熱輻射定律 (如方程式 2.274 所表示),發射率等於吸收率:
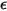 與吸收率
與吸收率 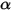 二者皆與出射光線與入射光線的波長無關。根據 Kirchhoff 熱輻射定律 (如方程式 2.274 所表示),發射率等於吸收率:
二者皆與出射光線與入射光線的波長無關。根據 Kirchhoff 熱輻射定律 (如方程式 2.274 所表示),發射率等於吸收率: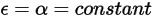
方程式 2.291
此外,假設存在漫射表面,則此表面上不會發生鏡面反射,並且此表面上入射輻射的反射度 (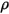 ) 相對於立體角而言具有同向性。根據方程式 2.290,表面反射度的計算方式如下:
) 相對於立體角而言具有同向性。根據方程式 2.290,表面反射度的計算方式如下:
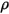 ) 相對於立體角而言具有同向性。根據方程式 2.290,表面反射度的計算方式如下:
) 相對於立體角而言具有同向性。根據方程式 2.290,表面反射度的計算方式如下: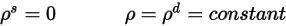
方程式 2.292
其中,
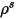 | 表面鏡面反射 |
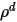 | 漫反射度 |
對於透明或半透明表面,透射率 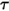 亦與波長無關:
亦與波長無關:
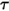 亦與波長無關:
亦與波長無關: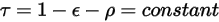
方程式 2.293
灰體漫射表面對表面模型假設表面之間的辐射能量交換幾乎不受分隔它們之介質的影響。因此,如果將一定量的辐射能量 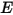 入射於每單位面積的表面上 (輻照度),則反射、吸收與透射的辐射能量分量分別為
入射於每單位面積的表面上 (輻照度),則反射、吸收與透射的辐射能量分量分別為 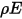 、
、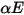 與
與 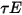 。對於大多數應用,表面對於紅外波譜中的熱輻射是不透明的,進而可將辐射表面視為不透明表面。因此,可以忽略透射率
。對於大多數應用,表面對於紅外波譜中的熱輻射是不透明的,進而可將辐射表面視為不透明表面。因此,可以忽略透射率 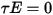 。根據方程式 2.273 與方程式 2.274,表面反射度
。根據方程式 2.273 與方程式 2.274,表面反射度 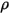 可表示如下:
可表示如下:
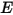 入射於每單位面積的表面上 (輻照度),則反射、吸收與透射的辐射能量分量分別為
入射於每單位面積的表面上 (輻照度),則反射、吸收與透射的辐射能量分量分別為 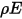 、
、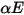 與
與 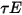 。對於大多數應用,表面對於紅外波譜中的熱輻射是不透明的,進而可將辐射表面視為不透明表面。因此,可以忽略透射率
。對於大多數應用,表面對於紅外波譜中的熱輻射是不透明的,進而可將辐射表面視為不透明表面。因此,可以忽略透射率 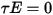 。根據方程式 2.273 與方程式 2.274,表面反射度
。根據方程式 2.273 與方程式 2.274,表面反射度 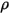 可表示如下:
可表示如下: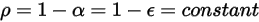
方程式 2.294
假設存在表面灰體漫射輻射,S2S 建模方程式會根據每個表面上的能量守恆來建構。
• S2S 建模方程式
S2S 模型的主要假設:封閉系統中辐射熱傳僅發生在灰體漫射表面之間 (灰體輻射)。可以忽略用於分隔曲面的介質中輻射的吸收、發射或散射。因此,針對數值分析,僅考量表面對表面輻射輻射。
離開指定表面的辐射能量通量由直接發射與反射之能量構成。反射的能量通量與來自外界的入射能量通量有關,從而可以用離開其他所有表面的能量通量來表示。若要計算表面的淨辐射能量流,為了便於計算,可以定義輻射度 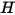 ,即每單位面積發射功率 (發射度)
,即每單位面積發射功率 (發射度) 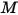 與表面每單位面積所接收輻射功率之反射分量 (輻照度)
與表面每單位面積所接收輻射功率之反射分量 (輻照度) 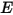 的總和:
的總和:
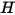 ,即每單位面積發射功率 (發射度)
,即每單位面積發射功率 (發射度) 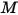 與表面每單位面積所接收輻射功率之反射分量 (輻照度)
與表面每單位面積所接收輻射功率之反射分量 (輻照度) 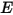 的總和:
的總和: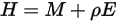
方程式 2.295
對於不透明表面 (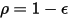 ),輻射度如下:
),輻射度如下:
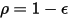 ),輻射度如下:
),輻射度如下: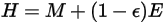
方程式 2.296
因此,根據 S2S 模型中的假設,可建構下列線性方程組來計算封閉系統中每個表面上的輻射度。假設 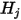 表示任意表面
表示任意表面 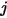 的輻射度,
的輻射度,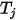 是表面溫度,且
是表面溫度,且 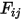 是表面
是表面 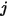 與
與  之間的視因子,則表面
之間的視因子,則表面  的輻射度如下:
的輻射度如下:
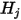 表示任意表面
表示任意表面 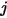 的輻射度,
的輻射度,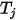 是表面溫度,且
是表面溫度,且 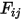 是表面
是表面 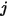 與
與  之間的視因子,則表面
之間的視因子,則表面  的輻射度如下:
的輻射度如下: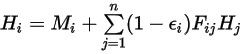
方程式 2.297
其中 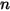 是參與辐射熱傳的表面數量。引入 Kronecker 符號
是參與辐射熱傳的表面數量。引入 Kronecker 符號 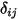 並對灰體輻射套用斯特凡-波茲曼定律 (方程式 2.278) 之後,可以重新整理方程式 2.297 並導出 S2S 建模方程式:
並對灰體輻射套用斯特凡-波茲曼定律 (方程式 2.278) 之後,可以重新整理方程式 2.297 並導出 S2S 建模方程式:
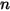 是參與辐射熱傳的表面數量。引入 Kronecker 符號
是參與辐射熱傳的表面數量。引入 Kronecker 符號 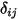 並對灰體輻射套用斯特凡-波茲曼定律 (方程式 2.278) 之後,可以重新整理方程式 2.297 並導出 S2S 建模方程式:
並對灰體輻射套用斯特凡-波茲曼定律 (方程式 2.278) 之後,可以重新整理方程式 2.297 並導出 S2S 建模方程式: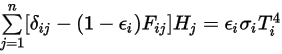
方程式 2.298
使用預先計算的視因子 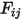 ,求解方程式 2.298 的線性方程組,可得到參與表面的
,求解方程式 2.298 的線性方程組,可得到參與表面的 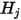 。然後,便可輕鬆計算出每個表面上的淨輻射熱流。對於表面
。然後,便可輕鬆計算出每個表面上的淨輻射熱流。對於表面  ,淨辐射熱流
,淨辐射熱流 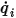 即每單位面積出射輻射 (
即每單位面積出射輻射 (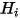 ) 與入射輻射 (
) 與入射輻射 (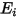 ) 之間的差值。根據方程式 2.278 和方程式 2.296,可以導出下列通量公式:
) 之間的差值。根據方程式 2.278 和方程式 2.296,可以導出下列通量公式:
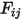 ,求解方程式 2.298 的線性方程組,可得到參與表面的
,求解方程式 2.298 的線性方程組,可得到參與表面的 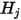 。然後,便可輕鬆計算出每個表面上的淨輻射熱流。對於表面
。然後,便可輕鬆計算出每個表面上的淨輻射熱流。對於表面  ,淨辐射熱流
,淨辐射熱流 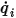 即每單位面積出射輻射 (
即每單位面積出射輻射 (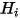 ) 與入射輻射 (
) 與入射輻射 (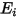 ) 之間的差值。根據方程式 2.278 和方程式 2.296,可以導出下列通量公式:
) 之間的差值。根據方程式 2.278 和方程式 2.296,可以導出下列通量公式: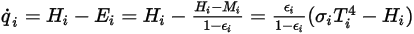
方程式 2.299
對於指定的表面積 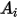 ,離開表面
,離開表面 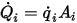 的淨輻射熱流計算如下:
的淨輻射熱流計算如下:
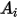 ,離開表面
,離開表面 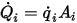 的淨輻射熱流計算如下:
的淨輻射熱流計算如下: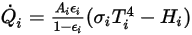
方程式 2.300
S2S 模型以方程式 2.298 形式的線性方程組組成。套用此模型的優點在於,對於指定的視因子與溫度,可藉由求解線性方程組計算系統來計算淨熱流 (透過套用數值演算法)。但是,套用提議的表面對表面模型時主要困難在於計算 n 個參與表面的 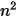 個視因子。此計算過程可能會非常耗時,尤其是隨著表面數量的增加,耗時可能會更多。
個視因子。此計算過程可能會非常耗時,尤其是隨著表面數量的增加,耗時可能會更多。
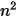 個視因子。此計算過程可能會非常耗時,尤其是隨著表面數量的增加,耗時可能會更多。
個視因子。此計算過程可能會非常耗時,尤其是隨著表面數量的增加,耗時可能會更多。視因子的計算
在 S2S 建模方程式 2.298 中,視因子 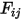 是指離開表面
是指離開表面  與撞擊表面
與撞擊表面 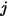 之輻射的占比。如圖 2.37 所示,假設
之輻射的占比。如圖 2.37 所示,假設 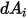 是表面
是表面  的微分面積,
的微分面積,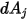 是表面
是表面 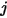 的微分面積,且
的微分面積,且 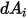 與
與 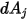 之間的距離是
之間的距離是 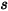 ,則在距離
,則在距離 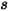 下,從
下,從 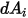 到
到 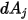 的視因子
的視因子 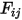 的表示如下所示:
的表示如下所示:
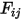 是指離開表面
是指離開表面  與撞擊表面
與撞擊表面 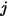 之輻射的占比。如圖 2.37 所示,假設
之輻射的占比。如圖 2.37 所示,假設 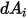 是表面
是表面  的微分面積,
的微分面積,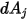 是表面
是表面 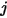 的微分面積,且
的微分面積,且 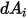 與
與 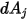 之間的距離是
之間的距離是 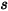 ,則在距離
,則在距離 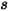 下,從
下,從 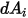 到
到 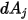 的視因子
的視因子 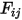 的表示如下所示:
的表示如下所示: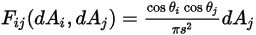
方程式 2.301
其中 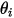 與
與 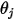 是表面法向與兩個微分面積之間的光線所成的角度。
是表面法向與兩個微分面積之間的光線所成的角度。
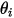 與
與 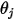 是表面法向與兩個微分面積之間的光線所成的角度。
是表面法向與兩個微分面積之間的光線所成的角度。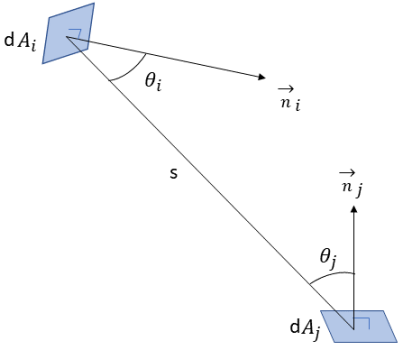
圖 2.37
如果 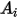 與
與 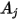 分別是表面
分別是表面  與
與 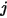 的指定面積,則從表面
的指定面積,則從表面  到表面
到表面 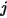 的視因子即方程式 2.301 對表面
的視因子即方程式 2.301 對表面  與
與 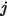 的平均面積積分:
的平均面積積分:
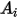 與
與 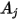 分別是表面
分別是表面  與
與 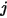 的指定面積,則從表面
的指定面積,則從表面  到表面
到表面 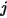 的視因子即方程式 2.301 對表面
的視因子即方程式 2.301 對表面  與
與 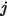 的平均面積積分:
的平均面積積分: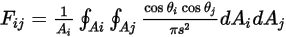
方程式 2.302
請注意,僅當兩個表面對彼此皆可見,或視因子為非零時,才會發生表面對表面輻射。針對 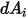 與
與 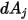 之間的可見度,引入 Kronecker 符號
之間的可見度,引入 Kronecker 符號 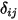 :
:
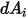 與
與 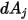 之間的可見度,引入 Kronecker 符號
之間的可見度,引入 Kronecker 符號 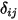 :
: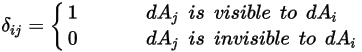
方程式 2.303
可以將方程式 2.302 重寫為:
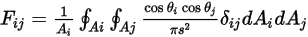
方程式 2.304
對於任何兩個對彼此皆可見的表面,指定表面  僅會將出射輻射能量的一部份輻射到表面
僅會將出射輻射能量的一部份輻射到表面 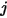 ,如圖 2.378 所示。因此,無因次視因子
,如圖 2.378 所示。因此,無因次視因子 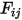 表示離開表面
表示離開表面  與到達表面
與到達表面 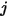 之能量的占比。這些特性會顯示在下列清單中:
之能量的占比。這些特性會顯示在下列清單中:
 僅會將出射輻射能量的一部份輻射到表面
僅會將出射輻射能量的一部份輻射到表面 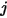 ,如圖 2.378 所示。因此,無因次視因子
,如圖 2.378 所示。因此,無因次視因子 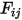 表示離開表面
表示離開表面  與到達表面
與到達表面 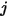 之能量的占比。這些特性會顯示在下列清單中:
之能量的占比。這些特性會顯示在下列清單中: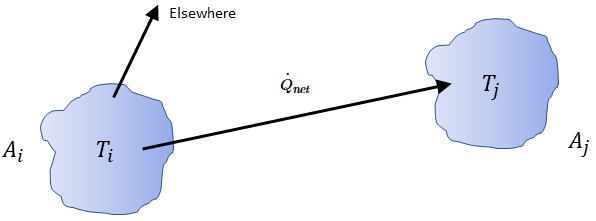
圖 2.378
• 視因子的總和 - 由於離開表面的輻射是守恆的,因此來自指定表面  之所有視因子的總和恒等於 1。對於
之所有視因子的總和恒等於 1。對於 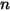 個表面構成的封閉系統,可以得到
個表面構成的封閉系統,可以得到
 之所有視因子的總和恒等於 1。對於
之所有視因子的總和恒等於 1。對於 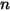 個表面構成的封閉系統,可以得到
個表面構成的封閉系統,可以得到
方程式 2.305
• 自身可見表面 - 由於輻射沿直線行進,因此,凸表面上的輻射光線無法在離開表面後再次撞擊同一表面。因此,凸表面自身不可見:
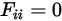
方程式 2.306
對於凹表面,來自表面上某一個位置的出射光線稍後會撞擊同一表面的不同位置。因此,凹表面對於自身是可見的:
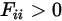
方程式 2.307
• 疊加 - 對於 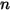 表面系統,如果指定的表面
表面系統,如果指定的表面  將能量輻射到
將能量輻射到 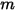 個表面 (
個表面 (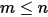 ),則表面
),則表面  與
與 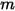 個表面之間的視因子等於表面
個表面之間的視因子等於表面  與
與 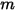 個表面之各個表面之間的視因子之和:
個表面之各個表面之間的視因子之和:
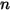 表面系統,如果指定的表面
表面系統,如果指定的表面  將能量輻射到
將能量輻射到 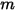 個表面 (
個表面 (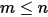 ),則表面
),則表面  與
與 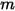 個表面之間的視因子等於表面
個表面之間的視因子等於表面  與
與 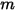 個表面之各個表面之間的視因子之和:
個表面之各個表面之間的視因子之和: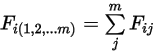
方程式 2.308
如果未針對幾何提供指定的圖表或圖形,此時疊加規則或求和規則很有用。疊加規則可供您使用已知的幾何之和或之差來表示正在追蹤的幾何。
• 互易性 - 方程式 2.304 將視因子 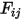 定義為離開表面
定義為離開表面  與到達表面
與到達表面 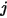 之辐射能量的占比。同樣地,視因子
之辐射能量的占比。同樣地,視因子 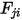 即指離開表面
即指離開表面 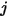 與到達表面
與到達表面  之能量的占比,其表示如下:
之能量的占比,其表示如下:
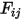 定義為離開表面
定義為離開表面  與到達表面
與到達表面 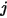 之辐射能量的占比。同樣地,視因子
之辐射能量的占比。同樣地,視因子 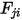 即指離開表面
即指離開表面 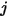 與到達表面
與到達表面  之能量的占比,其表示如下:
之能量的占比,其表示如下: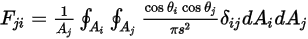
方程式 2.309
如果比較方程式 2.309 與方程式 2.304,可得到下列關係:
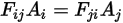
方程式 2.310
方程式 2.310 稱為視因子的互易性。此互易定理可讓您直接計算其中一個視因子對。
叢集
當輻射表面的數量非常大時,使用 S2S 輻射模型進行運算的成本很昂貴。欲縮短計算時間與降低儲存需求,可以透過對一定數量的鄰接邊界單元面進行分組來建立表面叢集,由此減少輻射表面的數量。然後,計算表面叢集的輻射度 (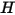 )。之後,再將這些值分配給每個叢集內的邊界單元面來計算壁溫度。由於輻射源項是高度非線性的 (與溫度的四次方成正比),請確定計算表面叢集的平均溫度,並使通量與源項在形成叢集的邊界面之間適當分佈。
)。之後,再將這些值分配給每個叢集內的邊界單元面來計算壁溫度。由於輻射源項是高度非線性的 (與溫度的四次方成正比),請確定計算表面叢集的平均溫度,並使通量與源項在形成叢集的邊界面之間適當分佈。
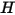 )。之後,再將這些值分配給每個叢集內的邊界單元面來計算壁溫度。由於輻射源項是高度非線性的 (與溫度的四次方成正比),請確定計算表面叢集的平均溫度,並使通量與源項在形成叢集的邊界面之間適當分佈。
)。之後,再將這些值分配給每個叢集內的邊界單元面來計算壁溫度。由於輻射源項是高度非線性的 (與溫度的四次方成正比),請確定計算表面叢集的平均溫度,並使通量與源項在形成叢集的邊界面之間適當分佈。表面叢集溫度是透過邊界面溫度的面積平均法求解得到的,如下列方程式所示:
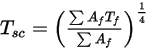
方程式 2.311
其中 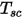 是表面叢集的溫度,
是表面叢集的溫度,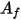 與
與 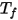 分別是 CFA 模擬中邊界單元面的面積與溫度。將針對表面叢集內的所有面執行求和運算。
分別是 CFA 模擬中邊界單元面的面積與溫度。將針對表面叢集內的所有面執行求和運算。
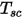 是表面叢集的溫度,
是表面叢集的溫度,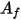 與
與 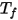 分別是 CFA 模擬中邊界單元面的面積與溫度。將針對表面叢集內的所有面執行求和運算。
分別是 CFA 模擬中邊界單元面的面積與溫度。將針對表面叢集內的所有面執行求和運算。