壁物理
壁的对数律:
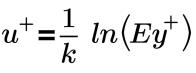
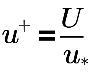
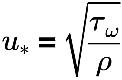
其中,
u+ | 无量纲速度 |
U | 局部 (单元中心) 速度 |
u* | 摩擦速度 |
τω | 壁剪切 |
ρ | 流体速度 |
E | 恒定系数 |
k | 冯卡曼常数 (0.41) |
y+ | 无量纲壁面与单元距离 |
壁函数和定律
壁函数可用于在无滑移边界 (壁) 处不存在极高密度网格分布时,对湍流边界层的近壁行为进行建模。文献中存在大量不同的壁函数,建议研究哪些壁函数适合于特定应用。壁函数用法为边界层理论主题 Schlichting (Boundary Layer Theory, 6th Edition, 1968 ISBN 07-055329-7)。
相邻流体中壁与点之间的无量纲距离 y+ 的定义如下所示:
其中,
摩擦速度 | |
v | 运动黏度 |
• 粘滞子层 0 < y+< 5
• 缓冲区层 5 < y+< 30
• 惯性层 30 < y+< 200
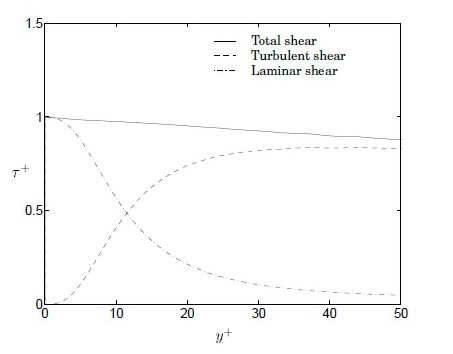
我们开发了多个壁函数,以用于支持所述的湍流黏度模型:
• “标准”(Standard) - 由 Launder 和 Spalding 提出,可定义近壁湍流平均速度剖面。使用“标准”(Standard) 壁函数的平均速度分布的壁定律如下所示:
在惯性子层和粘性子层中:
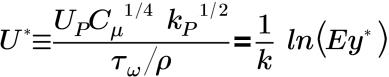
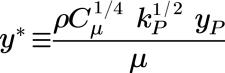
其中,
k=0.4187 | 冯卡曼常数 |
E=9.793 | 经验常数 |
UP | 点 P 处的流体的平均速度 |
kP | 点 P 处的湍流动能 |
yP | 点 P 与壁之间的距离 |
μ | 流体的动态黏度 |
“标准”(Standard) 壁函数适用于工业应用,并且还会在关于流体流动的文档中进行说明。该函数是在假设湍流动能产生量 K 与湍流能量耗散率保持局部平衡的情况下获得的。当预测流体具有较小压力梯度以及可忽略的加速或减速效果,但没有分离和回流时,“标准”(Standard) 壁函数最准确。
• “非平衡 (Kim)”(Nonequilibrium(Kim)) - 由 Kim 提出,可定义近壁湍流平均速度剖面。使用“非平衡 (Kim)”(Nonequilibrium(Kim)) 壁函数的平均速度分布的壁定律如下所示:
在惯性子层中:
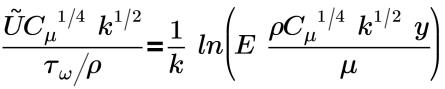
k=0.4187 | 冯卡曼常数 |
E=9.793 | 经验常数 |
UP | 点 P 处的流体的平均速度 |
kP | 点 P 处的流体的湍流动能平均速度 |
yP | 点 P 处的流体的湍流动能平均速度以及点 P 与壁之间的距离 |
μ | 点 P 处的流体的流体湍流动能平均速度动态黏度 |
Cμ | 0.09 |
“非平衡 (Kim)”(Nonequilibrium(Kim)) 壁函数可假定湍流动能产生率不等于耗散率。“非平衡 (Kim)”(Nonequilibrium(Kim)) 壁函数可考虑压力梯度效应。该函数使用双层模型处理粘性子层和全湍流惯性层。“非平衡 (Kim)”(Nonequilibrium(Kim)) 壁函数使用增强的壁处理方式,以在壁缓冲区 (3 < y+ < 10) 中使用混合函数,从而在粘性子层中的线性定律与惯性子层中的对数定律之间进行平滑过渡。
• “统一 (Shih)”(Unified(Shih)) - 由 Shih 提出,可跨边界层定义湍流平均速度剖面。使用“统一 (Shih)”(Unified(Shih)) 壁函数的平均速度分布的壁定律如下所示:
在整个边界层中,其中 f1(Yτ+) 和 f2(Yρ+) 为逐段拟合函数:
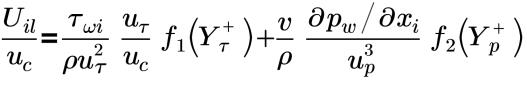
“统一 (Shih)”壁函数在粘性子层、缓冲层和惯性子层 (统一) 中有效。“统一 (Shih)”壁函数非常适用于具有顺压与逆压梯度的流体,以及具有加速度、减速度和回流的近壁面复杂流体。该壁函数使用三层模型处理粘性子层、缓冲层和惯性子层。
壁粗糙度模型
“壁粗糙度模型”(Wall Roughness Model) 指的是在壁上通过表面光洁度测量仪测得的粗糙度。
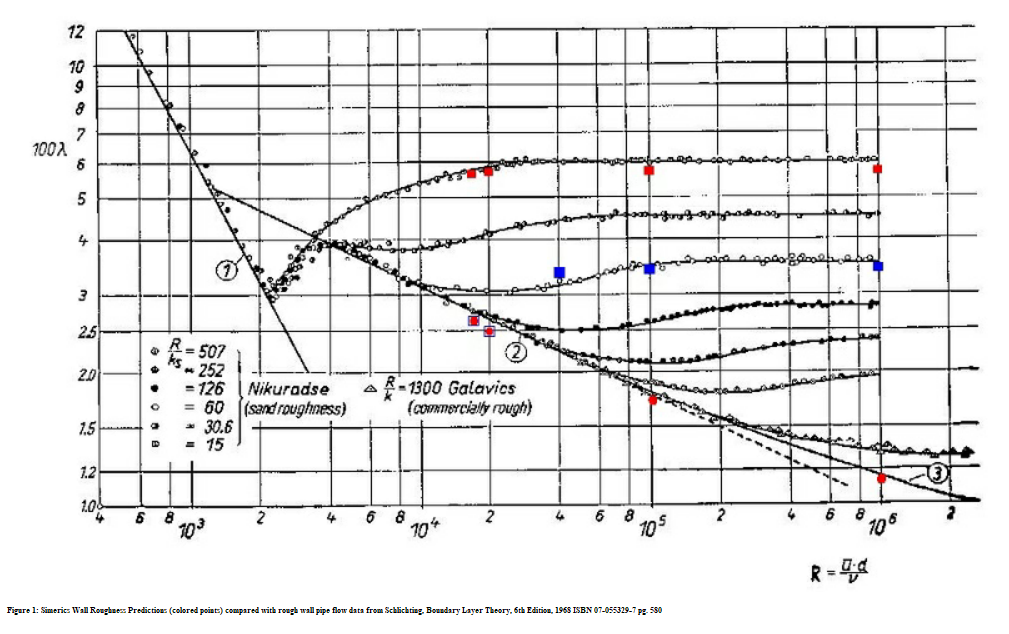
Creo Flow Analysis 壁粗糙度预测 (色点) 与粗壁管道流动数据进行比较 Schlichting, Boundary Layer Theory, 6th Edition, 1968 ISBN 07-055329-7 pg.580。