欧拉模型和控制方程
本部分介绍了流体体积 (VOF) 和多相混合模型的控制方程,可用于对多相流中的湍流和边界进行建模。
一般多相控制方程
在欧拉-欧拉 方法中,假定多相系统中的不同相或组分在数学上为互相贯穿的连续体,且具有相同的流动压力。由于物理空间或体积为所有相共用,因此我们引入相体积分数这一概念来描述相传输。假定相体积分数是空间和时间的连续函数,且其总和等于一。通过对每个相应用守恒定律推导出一个控制方程组,并利用理论或经验本构关系使该控制方程组封闭。欧拉-欧拉 方法定期使用的模型有两种类型:
• 非均匀或欧拉 多相流模型 - 直接对包括动量、能量、湍流和组分的相在内的每个相求解控制方程,以及体积分数方程。依据物理子模型对相间相互作用即动量、质量、组分和热的相间传递进行建模。
使用一般相标量 ϕq (其中 q 表示第 q 相) 表示时,q 相的广义方程具有以下形式:
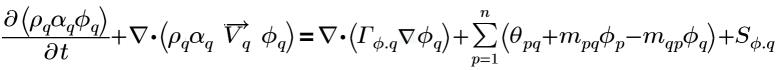
方程 2.54
其中,
ρq | q 密度 |
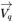 | 速度 |
Sϕq | 源项 |
Tϕq | 扩散系数 |
αq | 第 q 相的体积分数 |
以及 ϕq 表示多相系统的因变量:
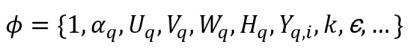
方程 2.55
其中,
Uq, Vq, Wq | 相速度分量 |
Hq | 相总焓 |
Yqi | 第 q 相中组分 "i" 的质量分数 |
k | 湍流动能 |
ε | k-ε 模型的湍流动能耗散率 |
在方程 2.54 中,右侧第二项表示相间交换。具体来说,
p | 第 p 相 |
n | 多相系统的相数 |
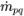 | 从第 q 相到第 p 相的质量传递 |
θpq | 传输量 (包括动量、能量和组分) 的直接相交换 |
利用相间组分、质量、动量和热交换的子模型,您可以从此处的广义传输方程推导出完整的流动控制方程组。
• 均匀多相模型 - 非均匀模型的简化和经济替代方案。均匀建模方法即对流动、能量和湍流的相控制方程求平均,以获得一个混合传输方程组,同时还会求解相体积分数。对于混合标量 ϕm,广义控制方程具有以下表达式:
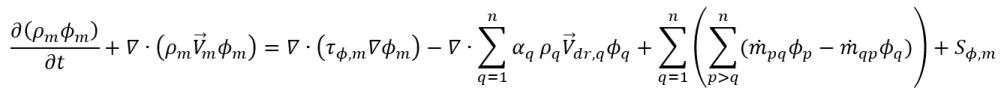
方程 2.56
其中,
m | 混合相 |
带有 m 下标的所有变量 | 混合相或相的平均值 |
以及 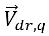 是 q 相速度和混合相速度的差值:
是 q 相速度和混合相速度的差值:
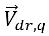 是 q 相速度和混合相速度的差值:
是 q 相速度和混合相速度的差值: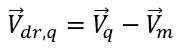
均匀多相模型是相间传递率较大的欧拉-欧拉多相流的极限情况。基本假定是所有相均具有相同的压力场。进一步假定所有相均具有公共的速度、温度和湍流场,在这种假定下,均匀模型进一步简化了完全非均匀欧拉 多相流模型。此方法易于实施且计算起来比较经济,是完整欧拉 多相流模型的一种很好的替代方法。在物理上,无需动量和能量方程的相间交换模型,均匀模型即可像完整的多相流模型一样,在自由表面流 (VOF)、空化或其他高度混合的多相流等情况下表现得很出色。
在 Creo Flow Analysis 中,当前多相模块仅采用均匀建模方法。重点关注对自由表面流 (流体体积模型) 和均匀液气两相流 (混合模型) 的建模。原则上,您可以应用 n 相流的建模功能。
VOF 和混合多相模型
流体体积 (VOF) 和混合多相模型均采用均匀建模方法。通过方程 2.54 求得每个相的体积分数传输方程。使用方程 2.56 以及质量、动量和能量守恒定律推导出混合相的动量和能量控制方程。控制方程组在本部分中进行了介绍。
• q 相体积分数方程
在方程 2.54 中,设 ϕq=1,将获得如下 q 相体积分数方程:
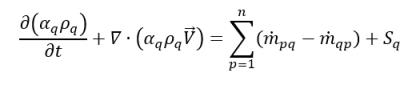
方程 2.57
其中,质量交换率项 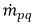 和
和 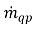 分别代表 q 相的源和汇的大小。在相面质量传递过程中,这两项中的其中一项通常为零。请参阅如下示例:
分别代表 q 相的源和汇的大小。在相面质量传递过程中,这两项中的其中一项通常为零。请参阅如下示例:
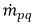 和
和 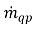 分别代表 q 相的源和汇的大小。在相面质量传递过程中,这两项中的其中一项通常为零。请参阅如下示例:
分别代表 q 相的源和汇的大小。在相面质量传递过程中,这两项中的其中一项通常为零。请参阅如下示例:在蒸发过程中,q 液相失去质量: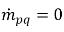 和
和 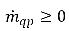 ,而对于 q 汽相:
,而对于 q 汽相: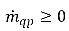 和
和 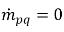 。
。
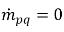 和
和 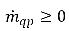 ,而对于 q 汽相:
,而对于 q 汽相: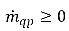 和
和 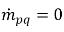 。
。对于 n 相系统,相体积分数的总和满足物理约束:
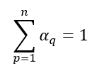
方程 2.58
或满足总质量守恒定律:
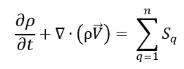
方程 2.59
其中混合量的定义如下所示:
◦ 体积平均混合密度
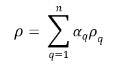
方程 2.60
◦ 质量平均混合速度
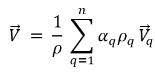
方程 2.61
• 混合相动量方程 - 通过对系统中所有相的各个动量方程求和,得到混合相的动量方程。从方程 2.56 中设置 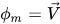 ,可得到
,可得到
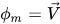 ,可得到
,可得到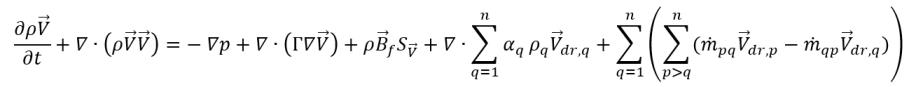
方程 2.62
其中混合量的定义如下所示:
◦ 体积平均混合黏度:

方程 2.63
使用混合相动力黏度 μ 和湍流黏度 μt 计算方程 2.62 中的扩散系数 Γ。右侧的后两项分别表示直接动量传递和由质量传递诱发的动量交换。它们由相漂移速度决定,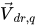 的定义如下:
的定义如下:
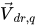 的定义如下:
的定义如下:
方程 2.69
在均匀建模方法中,您可以采用代数模型对此漂移速度进行建模。但是,在当前 VOF 和混合模型中,假定相间无滑动:
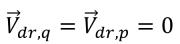
因此,动量交换项均为零。
◦ 混合能量方程
无速度滑动时,混合相的能量方程采用以下形式:
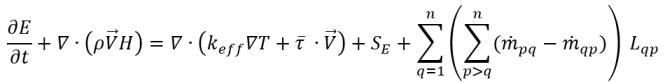
方程 2.70
其中混合量的定义如下所示:
▪ 体积平均热导系数
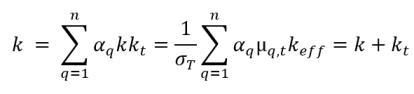
方程 2.71
▪ 质量平均混合能量和焓
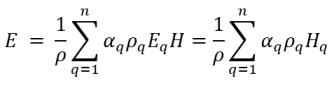
方程 2.72
在混合能量方程 2.70 中,粘滞发热项 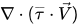 按单相流计算;SE 是总外部或用户热源。
按单相流计算;SE 是总外部或用户热源。
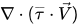 按单相流计算;SE 是总外部或用户热源。
按单相流计算;SE 是总外部或用户热源。右侧的最后一项为质量传递引起的界面热传递。假定相具有相同的温度,则 Lgp 取决于求解能量方程中 Hq 和 Hp 的定义。
如热模块中所述,材料的静态焓由两部分组成:标准状态参考焓和显焓。如果假定相 q 为液体,相 p 为蒸汽,则相总静态焓如下所示:
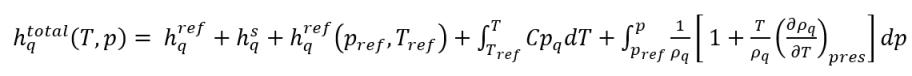
方程 2.73
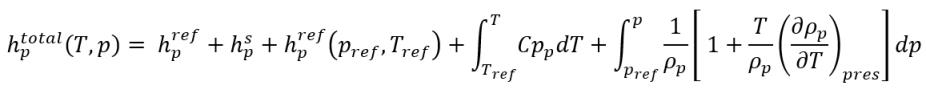
方程 2.74
其中,
pref | 参考压力 |
Tref | 参考温度 |
hq,ref | 相 q 标准状态参考焓 |
hp,ref | 相 p 标准状态参考焓 |
参考焓差
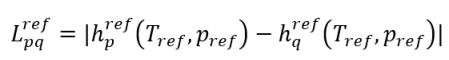
方程 2.75
为参考温度 Tref 和压力 pref 下的潜热。
▪ 包含标准参考焓:
在方程 2.70 中,如果焓 H 为总混合焓,则得到
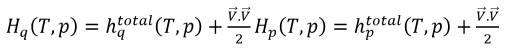
方程 2.76
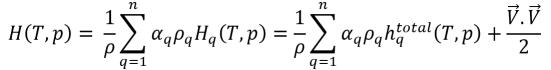
方程 2.77
则由于相形成焓或潜热所引起的差异,能量方程中已包括 Lpq。该数量设置为零:
Lpq=0
且由于质量传递所引起的热传递,方程 2.70 中右侧最后一项在混合能量方程中为零。
▪ 排除标准参考焓:
在 CFD 求解器中,不会直接求解总焓。而是仅相对于饱和温度的显焓会包含在求解的焓和内能中:
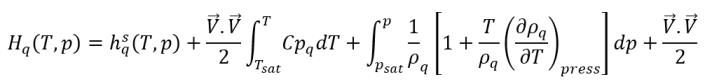
方程 2.79
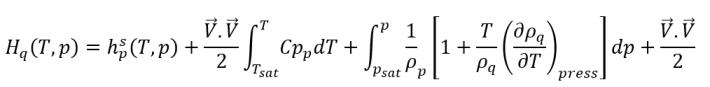
方程 2.80
则 Lpq 不为零。它应为潜热:
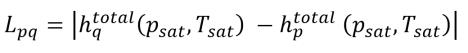
方程 2.81
其中,
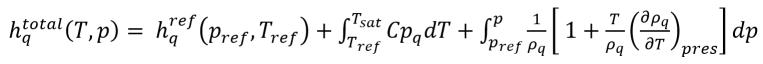
方程 2.82
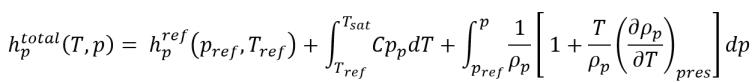
方程 2.83
在 Creo Flow Analysis 中,默认情况下将自动考虑标准状态参考焓。无需用户输入。
湍流模型
• 混合 k-ε 湍流模型
在流体体积 (VOF) 和混合多相模型中,采用扩展的单相湍流模型来解释湍流对混合相的影响。在 Creo Flow Analysis 中,将湍流模块中所述的湍流模型和近壁面处理扩展至多相流。采用混合流动后,标准和 RNG k-ε 模型将具有与单相湍流模型相同的一般形式:
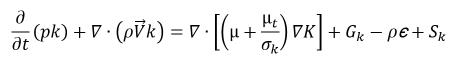
方程 2.84
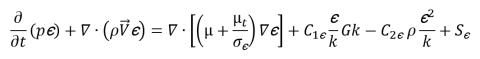
方程 2.85
其中,混合物密度 ρ、速度 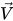 和分子黏度 μ 通过分别使用方程 2.60、2.61 和 2.63 中的关系以及各自的相值计算得出:Sk 和 Sε 同时包括可能的外部源和用户源以及相间作用源。混合物的湍流黏度 μt 直接从下列表达式计算得出:
和分子黏度 μ 通过分别使用方程 2.60、2.61 和 2.63 中的关系以及各自的相值计算得出:Sk 和 Sε 同时包括可能的外部源和用户源以及相间作用源。混合物的湍流黏度 μt 直接从下列表达式计算得出:
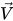 和分子黏度 μ 通过分别使用方程 2.60、2.61 和 2.63 中的关系以及各自的相值计算得出:Sk 和 Sε 同时包括可能的外部源和用户源以及相间作用源。混合物的湍流黏度 μt 直接从下列表达式计算得出:
和分子黏度 μ 通过分别使用方程 2.60、2.61 和 2.63 中的关系以及各自的相值计算得出:Sk 和 Sε 同时包括可能的外部源和用户源以及相间作用源。混合物的湍流黏度 μt 直接从下列表达式计算得出: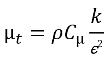
方程 2.86
而所产生的湍流动能则通过混合湍流黏度和速度梯度计算得出:
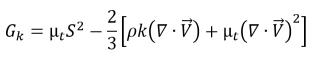
方程 2.87
其中 S 为应变平均混合率的模量,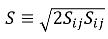
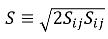
相 q 的湍流黏度可按如下所示计算:
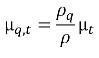
方程 2.87
• 湍流扩散效应
对于多相湍流流动,计算瞬时界面拖动项的平均值时会产生湍流扩散力,其作用与相扩散类似。不均匀欧拉 多流体模型通常将此湍流效应视为附加相间力,取决于相动量方程中的相体积分数梯度。但是,也可以通过直接将此湍流效应视为相体积分数方程中的湍流扩散项来对其进行建模。通过分割 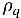 并将所有源分组为
并将所有源分组为 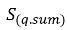 (相间质量传输和外部质量源的总和),湍流流动中将包含以下相 q 体积分数控制方程:
(相间质量传输和外部质量源的总和),湍流流动中将包含以下相 q 体积分数控制方程:
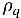 并将所有源分组为
并将所有源分组为 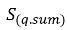 (相间质量传输和外部质量源的总和),湍流流动中将包含以下相 q 体积分数控制方程:
(相间质量传输和外部质量源的总和),湍流流动中将包含以下相 q 体积分数控制方程: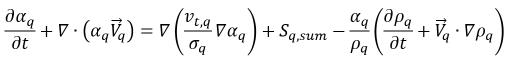
其中右侧第一项是相 q 中的湍流扩散项,必须符合以下约束,以满足总质量守恒:
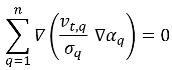
湍流扩散项通常作为一个选项实施。默认情况下,不包括此项。
多相边界建模
在流体体积 (VOF) 和混合多相模型中,流量和能量方程中的边界条件与单相流中的边界条件相同。这些内容将在流动和热模块中介绍。对于相体积分数,在下列情况下仅应用固定值和零梯度:
• n 相入口边界
对于 (n-1) 个相,入口体积分数是预先确定的,而第 n相是通过下列物理约束获得的:
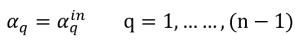
方程 2.88
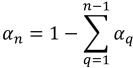
方程 2.89
并且每相的体积分数必须为非负数。
• 出口/对称/壁面边界
对于 (n–1) 个相,零梯度条件适用于所有出口、对称和壁边界,而第 n相是通过下列物理约束获得的:
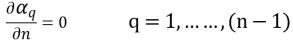
方程 2.90
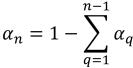
方程 2.91
上述控制方程、湍流模型和边界条件构成均匀 VOF 和混合多相模型的基础。如果没有外部或用户源项和相间质量传递,它们会构成一个封闭的方程组,且可以使用基于压力的有限体积多相求解器进行数值求解。在许多实际应用中,特定子模型 (如表面张力 VOF 模型和相间质量传递模型) 对于准确捕捉各自的物理现象和过程至关重要。建议直接将子模型包括在内置的模型中,而不是将其集中到外部或用户源。