About Internal Curves
Internal curves are curves that define a cross-sectional shape of a surface. Any number of internal curves can be added to a surface defined by boundaries, according to the following rules:
• You cannot add a COS as an internal curve.
• Internal curves cannot intersect consecutive (contignuous) boundaries in boundary surfaces, as shown in the following diagram.
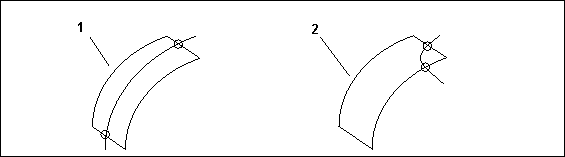
1. Correct
2. Incorrect
• Generally, internal curves must have soft points wherever they intersect the surface boundaries or other internal curves, as shown in the following diagram.
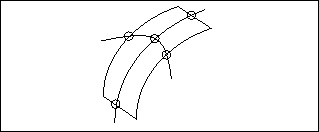
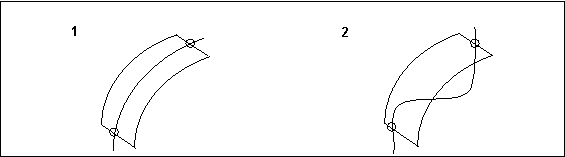
• If two internal curves cross the same borders in a boundary surface, they cannot intersect within the surface, as shown in the following diagram.
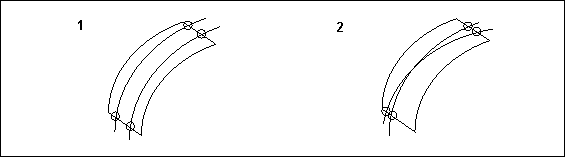
1. Correct
2. Incorrect
• The internal curve must intersect both borders of the surface, as shown in the following diagram.
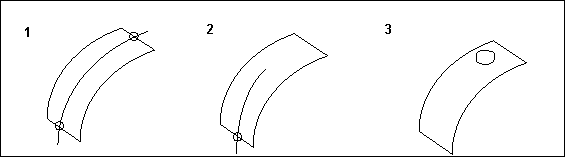
1. Correct
2. Incorrect
3. Incorrect
• An internal curve cannot intersect the surface boundary at more than two points, as shown in the following diagram.
1. Correct
2. Incorrect
• Internal curves in triangular surfaces may or may not intersect the natural boundary.
◦ An internal curve that intersects the natural boundary must pass through the degenerate vertex.
◦ An internal curve that does not intersect the natural boundary must intersect the other two boundaries.