Example: Geometric Tolerance Layout
Creo Parametric specifies a GTOL for an individual feature by means of a feature control frame (a rectangle) divided into compartments containing the GTOL symbol followed by the tolerance value. Where applicable, it also follows the tolerance with a material condition symbol.
If a GTOL is related to a datum, it places the reference datum name in a compartment following the tolerance value. Where applicable, it follows the datum reference letter with a material condition symbol.
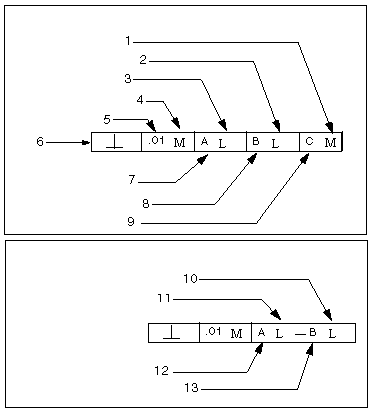
1. Matl Cond, Tertiary
2. Matl Cond, Secondary
3. Matl Cond, Primary
4. Matl Cond, Tolerance
5. Value
6. Type
7. Datum Ref, Primary
8. Datum Ref, Secondary
9. Datum Ref, Tertiary
10. Matl Cond, Primary, Compound
11. Matl Cond, Primary, Basic
12. Datum Ref, Primary, Basic
13. Datum Ref, Primary, Compound