물리
다성분 흐름의 경우 혼합물 속도, 압력, 온도, 터뷸런스 및 기타 물리적 수량에 대한 스칼라 전송 방정식을 계산합니다. 여러 컴포넌트가 있는 경우 추가 방정식을 풀어 유체 혼합물 내에서 컴포넌트를 어떻게 전송할 것인지 결정해야 합니다.
여러 화학종의 설명(컴포넌트)
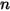 컴포넌트 흐름에서 컴포넌트
컴포넌트 흐름에서 컴포넌트  의 콘텐츠를 수량화할 수 있는 여러 가지 관련 변수가 있습니다.
의 콘텐츠를 수량화할 수 있는 여러 가지 관련 변수가 있습니다.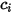 | 컴포넌트  의 몰 농도 의 몰 농도 |
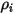 | 컴포넌트  의 질량 농도 의 질량 농도 |
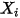 | 컴포넌트  의 몰 분율 의 몰 분율 |
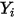 | 컴포넌트  의 질량 분율 의 질량 분율 |
4개의 수량은 다음과 같이 관련되어 있습니다.
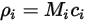
방정식 2.314
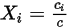
방정식 2.315
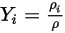
방정식 2.316
여기서 각 항목은 다음을 나타냅니다.
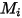 | 컴포넌트  의 분자 무게 의 분자 무게 |
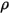 | 혼합물 밀도 |
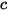 | 시스템에 있는 모든 컴포넌트의 몰 농도 합계: |
및
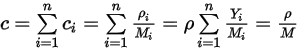
방정식 2.317
여기서 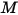 은 혼합물 분자 무게입니다.
은 혼합물 분자 무게입니다.
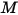 은 혼합물 분자 무게입니다.
은 혼합물 분자 무게입니다.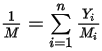
방정식 2.318
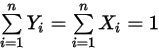
방정식 2.319
CFA 풀이 시스템에서는 편미분 전송 방정식을 직접 풀어 임의 컴포넌트 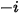 ,
, 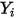 의 질량 분율을 구합니다. 다른 변수
의 질량 분율을 구합니다. 다른 변수 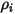 ,
, 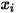 및
및 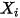 는 사후 처리에 사용하는 보조 변수입니다.
는 사후 처리에 사용하는 보조 변수입니다.
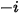 ,
, 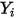 의 질량 분율을 구합니다. 다른 변수
의 질량 분율을 구합니다. 다른 변수 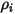 ,
, 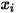 및
및 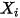 는 사후 처리에 사용하는 보조 변수입니다.
는 사후 처리에 사용하는 보조 변수입니다.지배 방정식
다성분 흐름에서 혼합물의 벌크 동작은 단일 속도, 압력, 온도 및 터뷸런스 필드를 사용하여 모델링됩니다. 화학종의 혼합 및 전송을 위해 각 컴포넌트에는 질량 보존에 대한 고유한 관리 방정식이 있습니다. 벌크 흐름에 있는 여러 컴포넌트의 영향은 컴포넌트 특성과 국소 질량 분율을 사용하여 밀도, 점도 같은 혼합물 특성의 변화를 통해 느낄 수 있습니다.
• 질량 분율 방정식
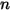 컴포넌트 혼합물 흐름에 대해 화학 반응이 없는 경우 임의 컴포넌트
컴포넌트 혼합물 흐름에 대해 화학 반응이 없는 경우 임의 컴포넌트  의 전송은 다음 방정식에 의해 제어됩니다.
의 전송은 다음 방정식에 의해 제어됩니다.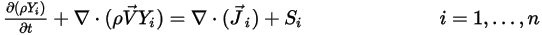
방정식 2.320
여기서 각 항목은 다음을 나타냅니다.
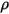 및 및 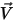 | 혼합물 밀도 및 속도 |
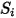 | 모든 사용자 정의 소스 |
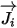 | 질량 확산 항 |
층류 흐름의 경우 속도 벡터 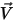 및 질량 분율
및 질량 분율 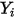 는 순간 변수입니다. 난류의 경우, 다성분 흐름이 가변 밀도 또는 압축성 흐름으로 간주되기 때문에 이러한 속도 벡터는 파브르 평균 수량입니다.
는 순간 변수입니다. 난류의 경우, 다성분 흐름이 가변 밀도 또는 압축성 흐름으로 간주되기 때문에 이러한 속도 벡터는 파브르 평균 수량입니다.
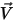 및 질량 분율
및 질량 분율 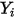 는 순간 변수입니다. 난류의 경우, 다성분 흐름이 가변 밀도 또는 압축성 흐름으로 간주되기 때문에 이러한 속도 벡터는 파브르 평균 수량입니다.
는 순간 변수입니다. 난류의 경우, 다성분 흐름이 가변 밀도 또는 압축성 흐름으로 간주되기 때문에 이러한 속도 벡터는 파브르 평균 수량입니다.방정식 2.320에서 혼합물 수량 및 질량 확산 항은 다음과 같이 정의됩니다.
◦ 혼합 밀도 - 모든 컴포넌트 밀도의 질량 평균 값입니다.
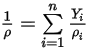
방정식 2.321
기체 화학종 혼합물의 경우 혼합물 밀도는 방정식 2.318을 통해 계산되는 혼합 분자 무게 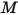 에 기초한 이상 기체 법칙을 사용하여 계산됩니다.
에 기초한 이상 기체 법칙을 사용하여 계산됩니다.
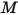 에 기초한 이상 기체 법칙을 사용하여 계산됩니다.
에 기초한 이상 기체 법칙을 사용하여 계산됩니다.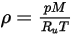
방정식 2.322
여기서 각 항목은 다음을 나타냅니다.
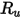 | 보편 기체 상수 |
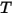 | 혼합물 온도 |
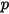 | 절대 압력 |
작동 압력(상수)을 사용하는 경우 방정식 2.322는 소위 말하는 비압축성 이상 기체 법칙으로 축소됩니다. 이는 작동 압력에 비해 게이지 압력이 종종 무시할 수 있는 화학종의 혼합 및 운반에 적절한 가정입니다.
◦ 혼합 속도 - 모든 컴포넌트 속도의 질량 평균 값입니다.
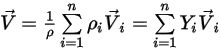
방정식 2.323
그러나 하나의 속도만 해결되므로 혼합 속도와 모든 컴포넌트 속도가 동일한 값을 갖는다고 가정합니다.
◦ 질량 확산 흐름 - 컴포넌트  의 질량 확산 흐름은 다음과 같이 층류 및 터뷸런스 확산 항 두 부분으로 구성됩니다.
의 질량 확산 흐름은 다음과 같이 층류 및 터뷸런스 확산 항 두 부분으로 구성됩니다.
 의 질량 확산 흐름은 다음과 같이 층류 및 터뷸런스 확산 항 두 부분으로 구성됩니다.
의 질량 확산 흐름은 다음과 같이 층류 및 터뷸런스 확산 항 두 부분으로 구성됩니다.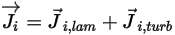
방정식 2.324
방정식 2.324에서 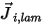 은 농도와 온도의 변화로 인해 발생하는 컴포넌트
은 농도와 온도의 변화로 인해 발생하는 컴포넌트  의 층류 확산 흐름입니다. 기본적으로 Creo Flow Analysis는 희석 근사 또는 픽의 법칙을 사용하여 농도 변화로 인한 질량 확산을 모델링합니다. 층류 확산 흐름에는 다음과 같은 공식이 있습니다.
의 층류 확산 흐름입니다. 기본적으로 Creo Flow Analysis는 희석 근사 또는 픽의 법칙을 사용하여 농도 변화로 인한 질량 확산을 모델링합니다. 층류 확산 흐름에는 다음과 같은 공식이 있습니다.
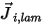 은 농도와 온도의 변화로 인해 발생하는 컴포넌트
은 농도와 온도의 변화로 인해 발생하는 컴포넌트  의 층류 확산 흐름입니다. 기본적으로 Creo Flow Analysis는 희석 근사 또는 픽의 법칙을 사용하여 농도 변화로 인한 질량 확산을 모델링합니다. 층류 확산 흐름에는 다음과 같은 공식이 있습니다.
의 층류 확산 흐름입니다. 기본적으로 Creo Flow Analysis는 희석 근사 또는 픽의 법칙을 사용하여 농도 변화로 인한 질량 확산을 모델링합니다. 층류 확산 흐름에는 다음과 같은 공식이 있습니다.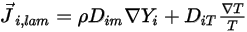
방정식 2.325
여기서 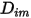 은 혼합물 내의 컴포넌트
은 혼합물 내의 컴포넌트  에 대한 질량 확산 계수이고
에 대한 질량 확산 계수이고 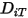 은 열(소레) 확산 계수입니다.
은 열(소레) 확산 계수입니다.
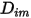 은 혼합물 내의 컴포넌트
은 혼합물 내의 컴포넌트  에 대한 질량 확산 계수이고
에 대한 질량 확산 계수이고 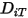 은 열(소레) 확산 계수입니다.
은 열(소레) 확산 계수입니다.난류의 경우, 방정식 2.320에서의 이류를 평균화하는 파브르에서 유도된 변동 항은 터뷸런스 확산으로 모델링됩니다.
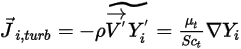
방정식 2.326
여기서 각 항목은 다음을 나타냅니다.
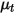 | 터뷸런스 점도 |
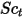 | 터뷸런스 슈미트 수 기본값: 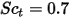 |
터뷸런스 확산은 일반적으로 층류 확산을 압도합니다. 난류에서 세부 층류 확산 특성의 사양은 일반적으로 터뷸런스 대응 항목보다 덜 중요합니다.
혼합물 흐름에 대한 질량 연속 방정식을 유도하려면 모든 컴포넌트 질량 분율 방정식을 더하고 방정식 2.319를 적용합니다.
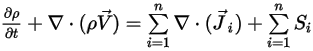
방정식 2.327
혼합물 흐름의 총 질량 보존을 만족시키기 위해 모든 컴포넌트에 대한 확산 항의 합은 0이어야 합니다.
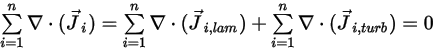
방정식 2.328
방정식 2.319 및 방정식 2.326에서 터뷸런스 확산 항은 항상 0으로 결정됩니다. 따라서 완전한 난류인 경우 일반적으로 방정식 2.328이 자동으로 충족되는 것으로 간주됩니다. 그러나 층류 흐름에 대해 또는 난류에서 층류 확산을 무시할 수 없는 경우 방정식 2.328은 다음과 같은 형태로 감소합니다.
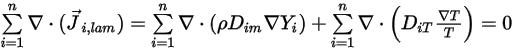
방정식 2.329
그런 다음 두 개의 개별 제약 조건을 적용하여 방정식 2.329를 충족합니다.
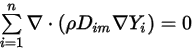
방정식 2.330
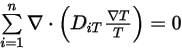
방정식 2.331
다성분 흐름의 연속성 방정식의 최종 형태는 다음과 같습니다.
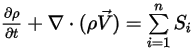
방정식 2.332
• 확산 계수
◦ 질량 확산 계수 - 층류 흐름에서의 질량 확산 흐름 공식인 방정식 2.325는 혼합물의 구성이 변경되지 않거나 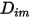 구성에 독립적인 경우에만 유효합니다. 이는
구성에 독립적인 경우에만 유효합니다. 이는 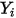 가 캐리어 기체를 제외한 모든 컴포넌트에 대해 매우 작은 경우 희석 혼합물에서 허용되는 근사값입니다. 다성분 층류 흐름에서 희석되지 않은 혼합물의 경우 다음 공식을 사용하여
가 캐리어 기체를 제외한 모든 컴포넌트에 대해 매우 작은 경우 희석 혼합물에서 허용되는 근사값입니다. 다성분 층류 흐름에서 희석되지 않은 혼합물의 경우 다음 공식을 사용하여 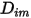 을 계산합니다.
을 계산합니다.
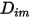 구성에 독립적인 경우에만 유효합니다. 이는
구성에 독립적인 경우에만 유효합니다. 이는 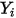 가 캐리어 기체를 제외한 모든 컴포넌트에 대해 매우 작은 경우 희석 혼합물에서 허용되는 근사값입니다. 다성분 층류 흐름에서 희석되지 않은 혼합물의 경우 다음 공식을 사용하여
가 캐리어 기체를 제외한 모든 컴포넌트에 대해 매우 작은 경우 희석 혼합물에서 허용되는 근사값입니다. 다성분 층류 흐름에서 희석되지 않은 혼합물의 경우 다음 공식을 사용하여 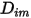 을 계산합니다.
을 계산합니다.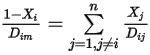
방정식 2.333
여기서 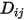 는 컴포넌트
는 컴포넌트 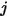 내에 있는 컴포넌트
내에 있는 컴포넌트  의 바이너리 질량 확산 계수로 지정하거나 계산해야 합니다.
의 바이너리 질량 확산 계수로 지정하거나 계산해야 합니다.
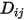 는 컴포넌트
는 컴포넌트 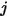 내에 있는 컴포넌트
내에 있는 컴포넌트  의 바이너리 질량 확산 계수로 지정하거나 계산해야 합니다.
의 바이너리 질량 확산 계수로 지정하거나 계산해야 합니다.◦ 지정된 값 - 바이너리 질량 확산 계수 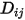 는 열 전송이 고려되는 경우 온도의 상수 또는 함수입니다. 값을 직접 지정하거나 지정된 슈미트 수에서 가져올 수 있습니다.
는 열 전송이 고려되는 경우 온도의 상수 또는 함수입니다. 값을 직접 지정하거나 지정된 슈미트 수에서 가져올 수 있습니다.
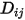 는 열 전송이 고려되는 경우 온도의 상수 또는 함수입니다. 값을 직접 지정하거나 지정된 슈미트 수에서 가져올 수 있습니다.
는 열 전송이 고려되는 경우 온도의 상수 또는 함수입니다. 값을 직접 지정하거나 지정된 슈미트 수에서 가져올 수 있습니다.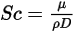
방정식 2.334
여기서 각 항목은 다음을 나타냅니다.
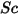 | 슈미트 수 |
슈미트 수는 분자(질량) 확산 속도에 대한 점성 확산 속도의 비율로 정의됩니다.
하나의 값 또는 하나의 온도 함수가 모든 컴포넌트에 적용되면 방정식 2.333이 다음과 같이 감소됩니다.
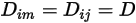
방정식 2.335
방정식 2.335는 농도가 높은 캐리어 흐름에서 낮은 질량 분율로 존재하는 화학종으로 희석된 혼합물을 모델링하는 데 적합한 근사값입니다. 이러한 경우 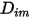 을 직접 상수 또는 온도 함수로 정의합니다.
을 직접 상수 또는 온도 함수로 정의합니다.
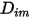 을 직접 상수 또는 온도 함수로 정의합니다.
을 직접 상수 또는 온도 함수로 정의합니다.◦ 운동학적 이론 - 이상 기체의 경우 바이너리 질량 확산 계수 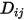 는 운동학적 이론을 사용하여 구할 수도 있습니다.
는 운동학적 이론을 사용하여 구할 수도 있습니다.
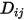 는 운동학적 이론을 사용하여 구할 수도 있습니다.
는 운동학적 이론을 사용하여 구할 수도 있습니다.참고 문헌: H. A. McGee, "Molecular Engineering", McGraw-Hill, New York, 1991.
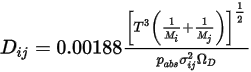
방정식 2.336
여기서 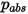 는 절대 압력이며,
는 절대 압력이며, 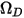 는 시스템에서 분자의 상호 작용을 측정하는 확산 충돌 적분입니다.
는 시스템에서 분자의 상호 작용을 측정하는 확산 충돌 적분입니다. 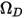 는 수량 함수
는 수량 함수 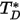 이며 다음과 같이 정의됩니다.
이며 다음과 같이 정의됩니다.
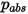 는 절대 압력이며,
는 절대 압력이며, 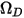 는 시스템에서 분자의 상호 작용을 측정하는 확산 충돌 적분입니다.
는 시스템에서 분자의 상호 작용을 측정하는 확산 충돌 적분입니다. 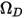 는 수량 함수
는 수량 함수 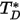 이며 다음과 같이 정의됩니다.
이며 다음과 같이 정의됩니다.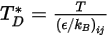
방정식 2.337
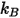 는 볼츠만 상수이며, 이 상수는 범용 기체 상수
는 볼츠만 상수이며, 이 상수는 범용 기체 상수 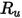 를 숫자로 나눈 값으로 정의됩니다. 혼합물의
를 숫자로 나눈 값으로 정의됩니다. 혼합물의 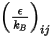 는 형상 평균입니다.
는 형상 평균입니다.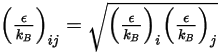
방정식 2.338
바이너리 혼합물의 경우 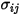 은 개별
은 개별 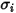 와
와 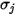 의 산술 평균으로 계산됩니다.
의 산술 평균으로 계산됩니다.
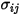 은 개별
은 개별 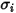 와
와 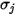 의 산술 평균으로 계산됩니다.
의 산술 평균으로 계산됩니다.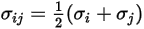
방정식 2.339
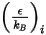 및
및 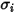 는 혼합물의
는 혼합물의  컴포넌트에 대한 레너드-존스 매개 변수입니다. 특히,
컴포넌트에 대한 레너드-존스 매개 변수입니다. 특히, 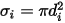 는 직경이
는 직경이 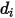 인 구 분자의 충돌 횡단면입니다. 분자는 직경이 두 배나 되는 영역을 스윕하고 충돌하는 분자도 직경이
인 구 분자의 충돌 횡단면입니다. 분자는 직경이 두 배나 되는 영역을 스윕하고 충돌하는 분자도 직경이 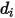 입니다.
입니다. 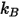 =1.38064852(79) ×10-23(J/K)는 볼츠만 상수입니다.
=1.38064852(79) ×10-23(J/K)는 볼츠만 상수입니다.Creo Flow Analysis에서는 두 개의 레너드-존스 매개 변수를 결정하기 위해 직경 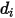 과 에너지
과 에너지 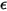 을 지정합니다.
을 지정합니다.
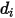 과 에너지
과 에너지 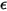 을 지정합니다.
을 지정합니다.◦ 열 확산 계수 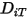 - 열 확산 계수는 상수, 온도의 다항식 함수, 사용자 정의 함수 또는 다음과 같이 아래의 참조에서 파생된 경험 기반의 구성 종속 표현식을 사용하여 정의할 수 있습니다.
- 열 확산 계수는 상수, 온도의 다항식 함수, 사용자 정의 함수 또는 다음과 같이 아래의 참조에서 파생된 경험 기반의 구성 종속 표현식을 사용하여 정의할 수 있습니다.
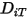 - 열 확산 계수는 상수, 온도의 다항식 함수, 사용자 정의 함수 또는 다음과 같이 아래의 참조에서 파생된 경험 기반의 구성 종속 표현식을 사용하여 정의할 수 있습니다.
- 열 확산 계수는 상수, 온도의 다항식 함수, 사용자 정의 함수 또는 다음과 같이 아래의 참조에서 파생된 경험 기반의 구성 종속 표현식을 사용하여 정의할 수 있습니다.참고 문헌: K. K. Y. Kuo, "Principles of Combustion", John Wiley and Sons, New York, 1986.
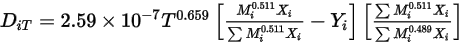
방정식 2.340
이러한 형태의 열 확산 계수는 무거운 분자가 가열된 서피스 쪽으로 더 느리게 확산되고 가벼운 분자가 더 빠르게 확산되도록 합니다.
• 운동량 방정식
질량 특성 및 속도의 경우 모든 컴포넌트의 혼합에 대한 운동량 방정식은 단일 유체 흐름에 대한 표현식과 동일한 표현식을 갖습니다.
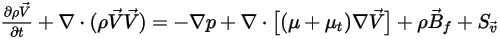
방정식 2.341
여기서는 방정식 2.321, 방정식 2.322 및 방정식 2.323을 사용하여 혼합 밀도와 속도가 계산됩니다. 터뷸런스 점도는 혼합 흐름을 기반으로 한 터뷸런스 모델로부터 직접 계산되므로 그 값은 컴포넌트에 독립적입니다. 층류 점도의 경우 다음과 같이 계산됩니다.
◦ 질량 평균 층류 점도 - 비이상 기체 혼합물의 경우 혼합물의 점도는 순수 화학종(컴포넌트) 점도의 질량 분율 평균을 기준으로 계산됩니다.
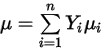
방정식 2.342
◦ 운동학적 이론 - 이상 기체 혼합물의 경우 혼합 점도는 운동학적 이론에 기초하여 계산됩니다. 각 컴포넌트의 역학 점도는 볼츠만 방정식을 기반으로 합니다.
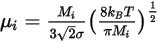
방정식 2.343
질량 확산도의 경우 혼합물의 기체 컴포넌트 점도를 계산하려면 레너드-존스 매개 변수 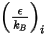 및
및 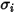 이 필요합니다.
이 필요합니다.
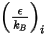 및
및 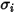 이 필요합니다.
이 필요합니다.이상적인 기체 혼합물에 대한 점도는 다음과 같이 계산됩니다.
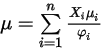
방정식 2.344
여기서 각 항목은 다음을 나타냅니다.
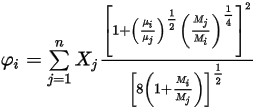
방정식 2.345
• 에너지 방정식
열 모듈에 설명된 대로 모든 구성의 혼합물에 대한 에너지 방정식은 다음과 같이 표현됩니다.
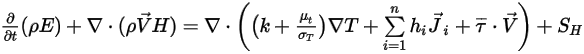
방정식 2.346
여기서 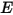 및
및 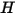 는
는 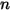 컴포넌트 혼합의 총 내부 에너지 및 총 엔탈피입니다. 혼합물별 열
컴포넌트 혼합의 총 내부 에너지 및 총 엔탈피입니다. 혼합물별 열 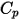 및 정적 엔탈피
및 정적 엔탈피 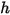 와 함께 각 컴포넌트의 해당 값을 질량 평균에 따라 구합니다.
와 함께 각 컴포넌트의 해당 값을 질량 평균에 따라 구합니다.
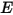 및
및 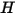 는
는 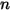 컴포넌트 혼합의 총 내부 에너지 및 총 엔탈피입니다. 혼합물별 열
컴포넌트 혼합의 총 내부 에너지 및 총 엔탈피입니다. 혼합물별 열 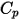 및 정적 엔탈피
및 정적 엔탈피 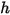 와 함께 각 컴포넌트의 해당 값을 질량 평균에 따라 구합니다.
와 함께 각 컴포넌트의 해당 값을 질량 평균에 따라 구합니다.◦ 질량 평균 혼합 열 용량
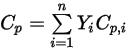
방정식 2.347
◦ 질량-평균 혼합물 에너지 및 엔탈피
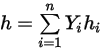
방정식 2.348
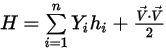
방정식 2.349
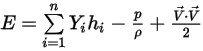
방정식 2.350
컴포넌트의 정적 엔탈피는 표준 상태 참조 엔탈피와 감지 엔탈피의 두 부분으로 구성됩니다. 다성분 흐름의 경우 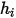 계산 시 엔탈피(절대값 또는 합계 값)의 두 부분을 모두 포함합니다.
계산 시 엔탈피(절대값 또는 합계 값)의 두 부분을 모두 포함합니다.
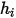 계산 시 엔탈피(절대값 또는 합계 값)의 두 부분을 모두 포함합니다.
계산 시 엔탈피(절대값 또는 합계 값)의 두 부분을 모두 포함합니다.방정식 2.336에서 오른쪽의 첫 번째 항은 에너지의 확산을 나타냅니다. 이는 열 전도, 화학종의 확산으로 인한 에너지 수송 및 점성 가열 세 부분으로 구성됩니다. 혼합물 열 전도의 경우 단일 유체 흐름과 동일한 방식으로 모델링됩니다. Creo Flow Analysis에서 혼합물 열 전도성은 다음과 같이 계산됩니다.
◦ 질량 평균 열 전도성 - 비이상 기체 혼합물의 경우 혼합물의 열 전도성은 순수 화학종 또는 컴포넌트 열 전도성의 단순 질량 분율 평균을 기반으로 계산됩니다.
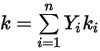
방정식 2.351
이것은 Creo Flow Analysis의 기본 방법입니다.
◦ 운동학적 이론 - 이상 기체 혼합물의 경우, 혼합물의 열 전도성은 운동학적 이론에 기초하여 계산될 수 있습니다. 각 컴포넌트에 대한 열 전도성 형식은 다음과 같습니다.
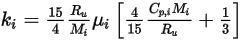
방정식 2.352
여기서 각 항목은 다음을 나타냅니다.
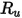 | 보편 기체 상수 |
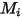 | 분자량 |
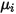 | 컴포넌트의 지정되거나 계산된 점도 |
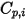 | 컴포넌트의 특정 또는 계산된 열 용량 |
층류 점도가 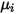 인 경우, 특정 열
인 경우, 특정 열 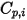 는 운동학적 이론을 사용하여 구할 수 있습니다.
는 운동학적 이론을 사용하여 구할 수 있습니다.
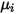 인 경우, 특정 열
인 경우, 특정 열 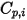 는 운동학적 이론을 사용하여 구할 수 있습니다.
는 운동학적 이론을 사용하여 구할 수 있습니다.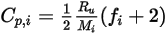
방정식 2.353
여기서 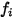 는 기체 컴포넌트
는 기체 컴포넌트  에 대한 에너지 스토리지(자유도)의 모드 수입니다.
에 대한 에너지 스토리지(자유도)의 모드 수입니다.
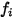 는 기체 컴포넌트
는 기체 컴포넌트  에 대한 에너지 스토리지(자유도)의 모드 수입니다.
에 대한 에너지 스토리지(자유도)의 모드 수입니다.이상 기체 혼합물의 열 전도성은 다음과 같이 계산됩니다.
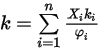
방정식 2.354
여기서 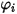 는 방정식 2.335으로 표현됩니다.
는 방정식 2.335으로 표현됩니다.
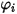 는 방정식 2.335으로 표현됩니다.
는 방정식 2.335으로 표현됩니다.두 번째 확산 항은 다음과 같습니다.
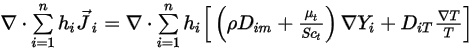
방정식 2.355
위의 항은 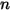 컴포넌트 흐름에서 화학종의 확산으로 인한 엔탈피의 전송을 나타냅니다. 이 항은 엔탈피 필드에 상당한 영향을 줄 수 있으므로 무시해서는 안 됩니다. 루이스 수(질량 확산도
컴포넌트 흐름에서 화학종의 확산으로 인한 엔탈피의 전송을 나타냅니다. 이 항은 엔탈피 필드에 상당한 영향을 줄 수 있으므로 무시해서는 안 됩니다. 루이스 수(질량 확산도 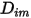 에 대한 열 확산도
에 대한 열 확산도 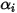 의 비율)가 다음과 같이 표시됩니다.
의 비율)가 다음과 같이 표시됩니다.
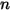 컴포넌트 흐름에서 화학종의 확산으로 인한 엔탈피의 전송을 나타냅니다. 이 항은 엔탈피 필드에 상당한 영향을 줄 수 있으므로 무시해서는 안 됩니다. 루이스 수(질량 확산도
컴포넌트 흐름에서 화학종의 확산으로 인한 엔탈피의 전송을 나타냅니다. 이 항은 엔탈피 필드에 상당한 영향을 줄 수 있으므로 무시해서는 안 됩니다. 루이스 수(질량 확산도 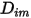 에 대한 열 확산도
에 대한 열 확산도 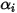 의 비율)가 다음과 같이 표시됩니다.
의 비율)가 다음과 같이 표시됩니다.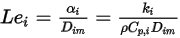
방정식 2.356
어떤 화학종도 1이 아니기 때문에 이 항을 무시하면 중대한 오류가 발생할 수 있습니다.
세 번째 확산 항은 점성 열 기여도 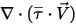 입니다. 단일 유체 흐름에서와 같은 방식으로 처리되지만 혼합 층류 및 터뷸런스 점도를 사용하여 전단
입니다. 단일 유체 흐름에서와 같은 방식으로 처리되지만 혼합 층류 및 터뷸런스 점도를 사용하여 전단 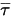 을 계산합니다. 일반 소스 항
을 계산합니다. 일반 소스 항 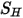 는 모든 컴포넌트에 대한 전체 외부 또는 사용자 열 소스입니다.
는 모든 컴포넌트에 대한 전체 외부 또는 사용자 열 소스입니다.
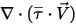 입니다. 단일 유체 흐름에서와 같은 방식으로 처리되지만 혼합 층류 및 터뷸런스 점도를 사용하여 전단
입니다. 단일 유체 흐름에서와 같은 방식으로 처리되지만 혼합 층류 및 터뷸런스 점도를 사용하여 전단 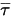 을 계산합니다. 일반 소스 항
을 계산합니다. 일반 소스 항 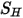 는 모든 컴포넌트에 대한 전체 외부 또는 사용자 열 소스입니다.
는 모든 컴포넌트에 대한 전체 외부 또는 사용자 열 소스입니다.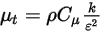
방정식 2.357
또한 터뷸런스 운동 에너지의 생산은 혼합물 터뷸런스 점도 및 속도 변화를 기반으로 계산됩니다.
다성분 경계 모델링
다성분 흐름에서 흐름, 에너지 및 터뷸런스 모델링 방정식에 대한 경계 조건은 흐름(Flow), 열(Heat) 및 터뷸런스(Turbulence) 모듈에서 설명한 단일 위상 흐름에 대한 경계 조건과 동일합니다. 컴포넌트 질량 분율의 경우 경계 조건은 지정된 값, 지정된 체적 유속 및/또는 변화로 구성됩니다.
• n 컴포넌트 유입구 경계
유입구 경계에서, 컴포넌트의 순 전송은 대류 및 확산 기여도로 구성될 수 있습니다. 대류는 지정된 유입구 화학종 질량 분율에 의해 결정됩니다. 확산은 계산된 질량 분율 필드의 변화에 따라 달라집니다. 대류 유입구 속도가 매우 느린 경우 확산으로 인해 유입구를 통해 상당량의 질량이 추가되거나 손실될 수 있습니다. 이러한 이유로 유입구 확산은 기본적으로 포함되지 않지만 옵션으로 활성화할 수 있습니다.

방정식 2.358
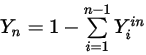
방정식 2.359
또한 각 컴포넌트의 질량 분율은 음수가 아니어야 합니다.
◦ 지정된 체적 유속 - 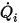 가 컴포넌트
가 컴포넌트  에 대해 미리 지정된 유입구 체적 유속인 경우 각 컴포넌트의 질량 흐름
에 대해 미리 지정된 유입구 체적 유속인 경우 각 컴포넌트의 질량 흐름 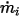 및 유입구
및 유입구 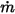 의 전체 질량 흐름은 다음과 같이 표시됩니다.
의 전체 질량 흐름은 다음과 같이 표시됩니다.
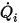 가 컴포넌트
가 컴포넌트  에 대해 미리 지정된 유입구 체적 유속인 경우 각 컴포넌트의 질량 흐름
에 대해 미리 지정된 유입구 체적 유속인 경우 각 컴포넌트의 질량 흐름 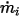 및 유입구
및 유입구 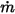 의 전체 질량 흐름은 다음과 같이 표시됩니다.
의 전체 질량 흐름은 다음과 같이 표시됩니다.
방정식 2.360
여기서 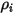 는 컴포넌트
는 컴포넌트  의 입구 밀도입니다.
의 입구 밀도입니다.
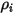 는 컴포넌트
는 컴포넌트  의 입구 밀도입니다.
의 입구 밀도입니다.정의에 따르면 질량 분율은 다음과 같이 계산됩니다.
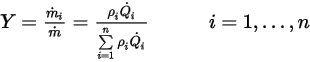
방정식 2.361
◦ 배출구, 대칭, 벽 경계 - 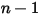 컴포넌트의 경우 모든 배출구, 대칭 및 벽 경계에 변화 0 조건이 적용되는 반면
컴포넌트의 경우 모든 배출구, 대칭 및 벽 경계에 변화 0 조건이 적용되는 반면 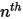 단계는 물리적 제약 조건을 사용하여 구합니다.
단계는 물리적 제약 조건을 사용하여 구합니다.
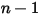 컴포넌트의 경우 모든 배출구, 대칭 및 벽 경계에 변화 0 조건이 적용되는 반면
컴포넌트의 경우 모든 배출구, 대칭 및 벽 경계에 변화 0 조건이 적용되는 반면 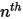 단계는 물리적 제약 조건을 사용하여 구합니다.
단계는 물리적 제약 조건을 사용하여 구합니다.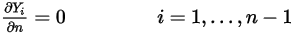
방정식 2.362
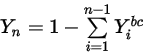
방정식 2.363
여기서 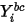 는 방정식 2.347에서 얻은 경계 값입니다.
는 방정식 2.347에서 얻은 경계 값입니다.
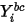 는 방정식 2.347에서 얻은 경계 값입니다.
는 방정식 2.347에서 얻은 경계 값입니다.수치 고려 사항
위의 지배 방정식, 터뷸런스 모델 및 경계 조건이 다성분 혼합 모델의 기초를 형성합니다. 외부 또는 사용자 소스 항 및 화학 반응이 없으면 압력 기반 유한 볼륨 풀이를 사용하여 수치를 계산하는 닫힌 연립 방정식입니다.
모든 컴포넌트에 대해 질량 분율 전송 방정식을 사용하여 풀 수 있습니다. 물리적 제약 조건을 충족시키기 위해 실제 질량 분율은 모든 컴포넌트 값의 합으로 조정됩니다.

방정식 2.364
여기서 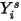 는 방정식 2.320을 풀어 얻은 값입니다. 실제 질량 분율은 다음과 같습니다.
는 방정식 2.320을 풀어 얻은 값입니다. 실제 질량 분율은 다음과 같습니다.
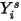 는 방정식 2.320을 풀어 얻은 값입니다. 실제 질량 분율은 다음과 같습니다.
는 방정식 2.320을 풀어 얻은 값입니다. 실제 질량 분율은 다음과 같습니다.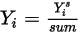
방정식 2.365
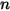 컴포넌트의 혼합물에도 적용된다는 것을 나타냅니다.
컴포넌트의 혼합물에도 적용된다는 것을 나타냅니다. 및 열 확산 계수
및 열 확산 계수 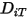 가 필요합니다.
가 필요합니다. 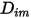 및
및 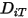 를 결정하는 방법은 다음과 같습니다.
를 결정하는 방법은 다음과 같습니다.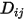 을 사용하여
을 사용하여 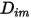 의 개별 질량 확산 계수를 계산합니다.
의 개별 질량 확산 계수를 계산합니다.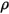 , 분자 점도
, 분자 점도 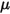 및 속도
및 속도 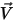 에 따라
에 따라 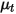 는 다음 표현식에서 직접 계산됩니다.
는 다음 표현식에서 직접 계산됩니다.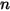 컴포넌트 흐름의 경우,
컴포넌트 흐름의 경우, 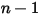 컴포넌트의 유입구 질량 분율은 미리 결정되는 반면,
컴포넌트의 유입구 질량 분율은 미리 결정되는 반면, 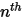 컴포넌트의 질량 분율은 물리적 제약 조건
컴포넌트의 질량 분율은 물리적 제약 조건