Physik
Die Bewegung masseloser Partikel wird auf der Grundlage des gelösten Strömungsfelds, der angegebenen Stromlinienberandung und den Freisetzungsbedingungen verfolgt, um Fluss-Stromlinien zu erzeugen.
Partikelbewegungsgleichung
Zur Verfolgung der Partikelbewegung werden die Bahnkurvengleichungen jedes Partikels analytisch oder numerisch gelöst (integriert). Für ein masseloses Partikel, das sich zusammen mit dem lokalen Strömungsfeld bewegt, wird die Bewegungsgleichung wie folgt umgeformt:
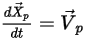
Gleichung 2.419
Dabei ist 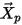 der Positionsvektor des Partikels, und die Partikelgeschwindigkeit
der Positionsvektor des Partikels, und die Partikelgeschwindigkeit 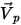 entspricht der Fließgeschwindigkeit an der Position
entspricht der Fließgeschwindigkeit an der Position  . Die Bahnkurve von
. Die Bahnkurve von  in der Strömungsdomäne ist dann eine Fluss-Stromlinie.
in der Strömungsdomäne ist dann eine Fluss-Stromlinie.
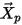 der Positionsvektor des Partikels, und die Partikelgeschwindigkeit
der Positionsvektor des Partikels, und die Partikelgeschwindigkeit 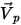 entspricht der Fließgeschwindigkeit an der Position
entspricht der Fließgeschwindigkeit an der Position  . Die Bahnkurve von
. Die Bahnkurve von  in der Strömungsdomäne ist dann eine Fluss-Stromlinie.
in der Strömungsdomäne ist dann eine Fluss-Stromlinie.Randbedingungen
Creo Flow Analysis wendet eine Stromlinien-Randbedingung an, um das Verhalten von Fluss-Stromlinien an einer Berandung zu bestimmen. Wenn sich Stromlinien an einer Berandung der Strömungsdomäne (einschließlich externen Berandungen und Fest-Flüssig-Schnittstellen) befinden, z.B. einer Wand oder einer Einlass-Berandung, kann an der Berandung eines der folgenden Ereignisse eintreten:
• Stromlinien werden reflektiert.
• Stromlinien können durch die Berandung eindringen, hinausgehen oder eindringen und hinausgehen.
• Stromlinien passieren durch eine interne Berandungszone, z.B. Lüfter (Fan) oder poröser Sprung (Porous Jump).
Auf der Basis des Stromlinienverhaltens an den Berandungen werden die Flow-Randbedingungen und Flow-Fest-Schnittstellen wiederum in drei Arten von Randbedingungen für Stromlinien gruppiert: "Offen" (Open), "Symmetrie" (Symmetry) und "Wand" (Wall).
• Offen (Open) – Stromlinien können die Rechendomäne verlassen, in diese eindringen oder diese verlassen und in diese eindringen. Eine offene Berandung ist normalerweise eine Einlass- oder Auslass-Berandung des Flüssigkeitsflusses. Sie kann auch auf Typen von Flow-Randbedingungen wie Wand und Symmetrie angewendet werden. An einer offenen Berandung kann die Stromlinie je nach Partikelgeschwindigkeitsrichtung (Fluss) die Domäne verlassen oder in diese eindringen.
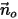 sei der Einheitsnormalenvektor zur offenen Berandung, der weg von der Rechendomäne zeigt. Bei der Partikelberandungsgeschwindigkeit
sei der Einheitsnormalenvektor zur offenen Berandung, der weg von der Rechendomäne zeigt. Bei der Partikelberandungsgeschwindigkeit 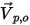 (entspricht der Fließgeschwindigkeit am Punkt) sind die folgenden Stromlinienbedingungen an der offenen Berandung vorhanden:
(entspricht der Fließgeschwindigkeit am Punkt) sind die folgenden Stromlinienbedingungen an der offenen Berandung vorhanden:◦ Wenn 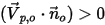 und der Geschwindigkeitsvektor
und der Geschwindigkeitsvektor  von der Rechendomäne zeigt. Dies gibt an, dass das Partikel oder der Fluss durch die Berandung entweicht. Das Partikel geht aus der Strömungsdomäne am Aufprallpunkt auf die Berandung verloren.
von der Rechendomäne zeigt. Dies gibt an, dass das Partikel oder der Fluss durch die Berandung entweicht. Das Partikel geht aus der Strömungsdomäne am Aufprallpunkt auf die Berandung verloren.
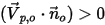 und der Geschwindigkeitsvektor
und der Geschwindigkeitsvektor  von der Rechendomäne zeigt. Dies gibt an, dass das Partikel oder der Fluss durch die Berandung entweicht. Das Partikel geht aus der Strömungsdomäne am Aufprallpunkt auf die Berandung verloren.
von der Rechendomäne zeigt. Dies gibt an, dass das Partikel oder der Fluss durch die Berandung entweicht. Das Partikel geht aus der Strömungsdomäne am Aufprallpunkt auf die Berandung verloren.◦ Wenn 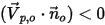 und der Geschwindigkeitsvektor
und der Geschwindigkeitsvektor  hin zur Rechendomäne zeigt. Dies gibt an, dass das Partikel oder der Fluss von der Berandung in die Domäne gelangt. Dieses Partikel wird zusammen mit dem Zufluss freigegeben oder in den Flüssigkeitsfluss von der offenen Berandung injiziert. Das Partikel ist ein Teil der Stromlinienberechnung am Punkt des Aufpralls auf die Berandung.
hin zur Rechendomäne zeigt. Dies gibt an, dass das Partikel oder der Fluss von der Berandung in die Domäne gelangt. Dieses Partikel wird zusammen mit dem Zufluss freigegeben oder in den Flüssigkeitsfluss von der offenen Berandung injiziert. Das Partikel ist ein Teil der Stromlinienberechnung am Punkt des Aufpralls auf die Berandung.
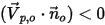 und der Geschwindigkeitsvektor
und der Geschwindigkeitsvektor  hin zur Rechendomäne zeigt. Dies gibt an, dass das Partikel oder der Fluss von der Berandung in die Domäne gelangt. Dieses Partikel wird zusammen mit dem Zufluss freigegeben oder in den Flüssigkeitsfluss von der offenen Berandung injiziert. Das Partikel ist ein Teil der Stromlinienberechnung am Punkt des Aufpralls auf die Berandung.
hin zur Rechendomäne zeigt. Dies gibt an, dass das Partikel oder der Fluss von der Berandung in die Domäne gelangt. Dieses Partikel wird zusammen mit dem Zufluss freigegeben oder in den Flüssigkeitsfluss von der offenen Berandung injiziert. Das Partikel ist ein Teil der Stromlinienberechnung am Punkt des Aufpralls auf die Berandung.• Symmetrie (Symmetry) – Stromlinien werden an der Berandung reflektiert. Für Stromlinien entspricht eine Symmetrieberandung normalerweise der Fluss-Symmetrie. Sie kann auch eine Position für die Freisetzung oder das Entwickeln von Partikeln sein, so wie dies auch bei der offenen Stromlinien-Berandung der Fall ist.
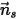 sei der Einheitsvektor normal zur Symmetrie am Punkt
sei der Einheitsvektor normal zur Symmetrie am Punkt 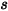 der Symmetrieberandung, der weg von der Symmetrie hin zur Rechendomäne zeigt. Ferner werden
der Symmetrieberandung, der weg von der Symmetrie hin zur Rechendomäne zeigt. Ferner werden 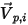 und
und 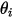 eingeführt, um den Winkel der Partikel-Aufprallgeschwindigkeit (lokale Fließgeschwindigkeit) an der Symmetrie-Partikelberandung anzugeben, wie in der folgenden Abbildung dargestellt. Da das Partikel von der Symmetrieberandung reflektiert wird, bleibt die tangentiale Geschwindigkeit gleich, während die normale Geschwindigkeitskomponente nur das Vorzeichen ändert. Mathematisch wird die Partikel- oder Stromlinien-Symmetrierandungbedingung in folgender Weise ausgedrückt:
eingeführt, um den Winkel der Partikel-Aufprallgeschwindigkeit (lokale Fließgeschwindigkeit) an der Symmetrie-Partikelberandung anzugeben, wie in der folgenden Abbildung dargestellt. Da das Partikel von der Symmetrieberandung reflektiert wird, bleibt die tangentiale Geschwindigkeit gleich, während die normale Geschwindigkeitskomponente nur das Vorzeichen ändert. Mathematisch wird die Partikel- oder Stromlinien-Symmetrierandungbedingung in folgender Weise ausgedrückt: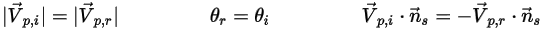
Gleichung 2.420
Dabei gilt:
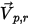 | Geschwindigkeit der Reflexion des Partikels |
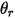 | Winkel an Punkt 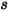 der Symmetrieberandung der Symmetrieberandung |
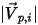 | Geschwindigkeitsbetrag |
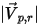 | Geschwindigkeitsbetrag |
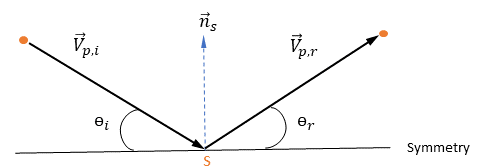
Abbildung
Da sich masselose Partikel mit der lokalen Fließgeschwindigkeit bewegen, die durch Fluss-Simulationen ermittelt wird, ist keine Randbedingung erforderlich, wenn die Gleichung 2.419 an einer Stromlinien-Symmetrieberandung integriert wird.
• Stromlinienrandbedingung "Wand" (Wall)
Für Stromlinien entspricht eine Wand-Stromlinienrandbedingung normalerweise der Flow-Randbedingung "Wand" (Wall). An einer Wand-Stromlinienrandbedingung bewegen sich die masselosen Partikel mit dem Flüssigkeitsfluss. Da die lokale Fließgeschwindigkeit und somit die Partikelgeschwindigkeit mit den entsprechenden wandnahen Modellen ermittelt werden, ist keine explizite Wand-Randbedingung erforderlich, um die Gleichung 2.419 zu lösen.
Wand-Stromlinienrandbedingungen können externe Wände und Flüssig-Fest-Schnittstellen sein. Für die Stromlinien-Randbedingungen "Offen" (Open) und "Symmetrie" (Symmetry) kann eine Wand-Stromlinienrandbedingung auch eine Position für die Partikelfreisetzung sein.
Partikelfreisetzung
Die von einer angegebenen Stromlinien-Berandung freigesetzten Partikel liefern die Anfangsbedingungen und Werte für die Stromlinien. Wie bei der Lagrange-Partikelverfolgung beinhaltet das Verfahren zum Bestimmen der Anfangsbedingungen die Partikelfreisetzung (Richtung, Position, Anzahl der Partikel und Verteilung) von Berandungen (Offen, Symmetrie, Wand und Schnittstelle) und die Zuweisung von Eigenschaften für jedes Partikel.
Bei Stromlinien wird die Anfangsgeschwindigkeit jedes masselosen Partikels 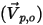 an seiner Freisetzungsposition
an seiner Freisetzungsposition 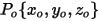 automatisch auf die lokale Fließgeschwindigkeit
automatisch auf die lokale Fließgeschwindigkeit 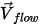 eingestellt. In Creo Flow Analysis wird mit den Optionen für Release Particle die Freisetzung von Stromlinien-Partikeln gesteuert.
eingestellt. In Creo Flow Analysis wird mit den Optionen für Release Particle die Freisetzung von Stromlinien-Partikeln gesteuert.
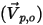 an seiner Freisetzungsposition
an seiner Freisetzungsposition 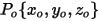 automatisch auf die lokale Fließgeschwindigkeit
automatisch auf die lokale Fließgeschwindigkeit 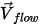 eingestellt. In Creo Flow Analysis wird mit den Optionen für Release Particle die Freisetzung von Stromlinien-Partikeln gesteuert.
eingestellt. In Creo Flow Analysis wird mit den Optionen für Release Particle die Freisetzung von Stromlinien-Partikeln gesteuert.Animation von Stromlinien
Die Bahnkurvengleichung jedes Partikels, Gleichung 2.419, wird gelöst oder numerisch integriert, um die Fluss-Stromlinien als Kurven zu erzeugen und zu visualisieren. Bei den Fluss-Lösungen ist der Partikel- oder Fließgeschwindigkeitswert bekannt, und Sie berechnen die Partikelverschiebung mithilfe der Euler-Vorwärts-Integration der Partikelgeschwindigkeit über die Animationszeitgröße 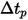 :
:
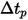 :
:
Gleichung 2.421
Dabei gilt:
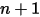 | neue Werte |
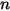 | aktuelle Werte |
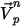 | Partikelgeschwindigkeit (lokaler Fluss) |
Beim ersten Zeitschritt ist 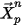 die Freisetzungsposition und
die Freisetzungsposition und 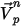 die Freisetzungsgeschwindigkeit:
die Freisetzungsgeschwindigkeit:
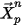 die Freisetzungsposition und
die Freisetzungsposition und 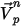 die Freisetzungsgeschwindigkeit:
die Freisetzungsgeschwindigkeit:
Gleichung 2.422
Beachten Sie, dass der benutzerdefinierte Animationszeitschritt 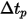 ein reeller Zahlenmultiplikator ist, der zur Animation der Stromlinien verwendet wird. Der Wert 1 gibt an, dass die Animationskurven dieselbe Geschwindigkeit wie die lokale Geschwindigkeit aufweisen. Der Wert von
ein reeller Zahlenmultiplikator ist, der zur Animation der Stromlinien verwendet wird. Der Wert 1 gibt an, dass die Animationskurven dieselbe Geschwindigkeit wie die lokale Geschwindigkeit aufweisen. Der Wert von  ändert die Kurven-Fließgeschwindigkeit in
ändert die Kurven-Fließgeschwindigkeit in 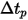 -mal die lokale Fließgeschwindigkeit.
-mal die lokale Fließgeschwindigkeit.
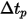 ein reeller Zahlenmultiplikator ist, der zur Animation der Stromlinien verwendet wird. Der Wert 1 gibt an, dass die Animationskurven dieselbe Geschwindigkeit wie die lokale Geschwindigkeit aufweisen. Der Wert von
ein reeller Zahlenmultiplikator ist, der zur Animation der Stromlinien verwendet wird. Der Wert 1 gibt an, dass die Animationskurven dieselbe Geschwindigkeit wie die lokale Geschwindigkeit aufweisen. Der Wert von  ändert die Kurven-Fließgeschwindigkeit in
ändert die Kurven-Fließgeschwindigkeit in 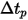 -mal die lokale Fließgeschwindigkeit.
-mal die lokale Fließgeschwindigkeit.Sie können außerdem den Durchmesser der Stromlinienkurven als Liniendicke (Line Thickness) angeben. Die Länge einer Stromlinienkurve ist gleich der lokalen Geschwindigkeit multipliziert mit dem Animationszeitschritt: 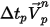 . Sie können die Benutzereingabe Maximale integrale Schritte (Maximum Integral Steps) einführen, um einzuschränken, wie weit der Stromlinien-Algorithmus zur Verfolgung einer Stromlinie verwendet wird, um zu verhindern, dass beim Stromlinienverfolgungsverfahren sehr viel Rechenzeit für die Verfolgung einer Stromlinie aufgewendet wird, die entweder in Schleifen verläuft oder stagniert. Ein kleiner Wert verkürzt die Rechenzeit, wobei ein sehr kleiner Wert eine Stromlinie zu früh beenden kann.
. Sie können die Benutzereingabe Maximale integrale Schritte (Maximum Integral Steps) einführen, um einzuschränken, wie weit der Stromlinien-Algorithmus zur Verfolgung einer Stromlinie verwendet wird, um zu verhindern, dass beim Stromlinienverfolgungsverfahren sehr viel Rechenzeit für die Verfolgung einer Stromlinie aufgewendet wird, die entweder in Schleifen verläuft oder stagniert. Ein kleiner Wert verkürzt die Rechenzeit, wobei ein sehr kleiner Wert eine Stromlinie zu früh beenden kann.
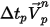 . Sie können die Benutzereingabe Maximale integrale Schritte (Maximum Integral Steps) einführen, um einzuschränken, wie weit der Stromlinien-Algorithmus zur Verfolgung einer Stromlinie verwendet wird, um zu verhindern, dass beim Stromlinienverfolgungsverfahren sehr viel Rechenzeit für die Verfolgung einer Stromlinie aufgewendet wird, die entweder in Schleifen verläuft oder stagniert. Ein kleiner Wert verkürzt die Rechenzeit, wobei ein sehr kleiner Wert eine Stromlinie zu früh beenden kann.
. Sie können die Benutzereingabe Maximale integrale Schritte (Maximum Integral Steps) einführen, um einzuschränken, wie weit der Stromlinien-Algorithmus zur Verfolgung einer Stromlinie verwendet wird, um zu verhindern, dass beim Stromlinienverfolgungsverfahren sehr viel Rechenzeit für die Verfolgung einer Stromlinie aufgewendet wird, die entweder in Schleifen verläuft oder stagniert. Ein kleiner Wert verkürzt die Rechenzeit, wobei ein sehr kleiner Wert eine Stromlinie zu früh beenden kann.