Modellierung der Strahlungswärmeübertragung
In einem thermischen Fluidsystem können die Körperflächen, der Flüssigkeitsfluss oder sowohl die Körperflächen als auch der Flüssigkeitsfluss aufgrund von Strahlung einer Erwärmung oder Kühlung ausgesetzt sein. In CFA-Modellen wird die Strahlungswärmeübertragung durch Lösen der Strahlungstransportgleichung (RTE) und anschließendes Abrufen des Strahlungsquellterms für die Gesamtenergie-Erhaltungsgleichung erläutert. Ein häufig verwendeter Modellierungsansatz, das Surface-to-Surface-Strahlungsmodell (S2S), ist das in Creo Flow Analysis gewählte Modell.
Strahlungstransportgleichung
Wenn ein Strahlungsstrahl eine Schicht eines absorbierenden, emittierenden und streuenden Mediums in einer bestimmten Richtung durchquert, verliert der Strahl Energie sowohl durch Absorption als auch durch Streuung weg vom Strahl. Der Strahl gewinnt auch Energie von Lichtquellen im Medium durch Emission und die Streuung, die hin zum Strahl gerichtet ist. Die Gesamtenergie-Bilanz des Strahls über eine unendliche Schicht des Mediums hinweg resultiert in einer Differentialgleichung, die als Strahlungstransportgleichung (RTE) bezeichnet wird.
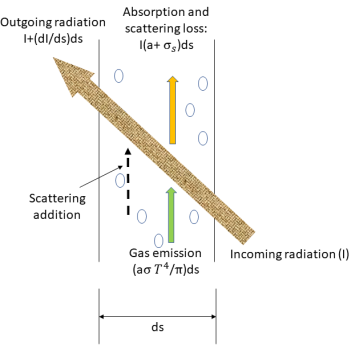
Zur Ableitung der Strahlungstransportgleichung sollten Sie davon ausgehen, dass ein eingehender Strahlungsstrahl mit der Intensität I ein Medium, z.B. ein Gas, mit der inkrementellen Dicke ds in Richtung 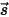 durchläuft, wie in der Abbildung dargestellt. Durch die Mediumschicht hindurch ändern sich die Inzidenz an der Position
durchläuft, wie in der Abbildung dargestellt. Durch die Mediumschicht hindurch ändern sich die Inzidenz an der Position 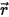 und die Richtung
und die Richtung 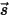 auf vier Arten, durch die die Strahlungsintensität
auf vier Arten, durch die die Strahlungsintensität 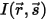 entweder erhöht (Energiegewinn +) oder verringert (Energieverlust –) wird:
entweder erhöht (Energiegewinn +) oder verringert (Energieverlust –) wird:
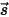 durchläuft, wie in der Abbildung dargestellt. Durch die Mediumschicht hindurch ändern sich die Inzidenz an der Position
durchläuft, wie in der Abbildung dargestellt. Durch die Mediumschicht hindurch ändern sich die Inzidenz an der Position 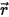 und die Richtung
und die Richtung 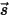 auf vier Arten, durch die die Strahlungsintensität
auf vier Arten, durch die die Strahlungsintensität 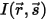 entweder erhöht (Energiegewinn +) oder verringert (Energieverlust –) wird:
entweder erhöht (Energiegewinn +) oder verringert (Energieverlust –) wird:• Absorption – Ein Medium, z.B. Gas, absorbiert einen Anteil der Strahlung, die durch dieses hindurchläuft. Mit dem Absorptionskoeffizienten 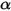 ist die Strahlungsenergie, die durch Absorption verloren geht:
ist die Strahlungsenergie, die durch Absorption verloren geht:
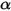 ist die Strahlungsenergie, die durch Absorption verloren geht:
ist die Strahlungsenergie, die durch Absorption verloren geht: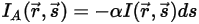
Gleichung 2.282
• Streuung – Ein Medium, z.B. Gas, streut einen Anteil der Strahlungsenergie in eine andere Richtung (weg von der Richtung 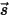 ), wenn der Strahl durch das Medium hindurchläuft. Mit dem Streuungskoeffizienten
), wenn der Strahl durch das Medium hindurchläuft. Mit dem Streuungskoeffizienten 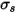 ist die Strahlungsenergie, die durch Streuung verloren geht:
ist die Strahlungsenergie, die durch Streuung verloren geht:
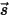 ), wenn der Strahl durch das Medium hindurchläuft. Mit dem Streuungskoeffizienten
), wenn der Strahl durch das Medium hindurchläuft. Mit dem Streuungskoeffizienten 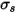 ist die Strahlungsenergie, die durch Streuung verloren geht:
ist die Strahlungsenergie, die durch Streuung verloren geht: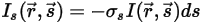
Gleichung 2.283
• Emission – Ein Medium emittiert Strahlungsenergie hin zu dem Strahl als grauer Körper gemäß seiner lokalen Temperatur (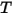 ) und den Emissionseigenschaften des Strahls. Aus dem Stefan-Boltzmann-Gesetz und der Reziprozität von Emission und Absorption, Gleichung 2.274 und Gleichung 2.279, ergibt sich für die vom Medium emittierte Strahlung:
) und den Emissionseigenschaften des Strahls. Aus dem Stefan-Boltzmann-Gesetz und der Reziprozität von Emission und Absorption, Gleichung 2.274 und Gleichung 2.279, ergibt sich für die vom Medium emittierte Strahlung: 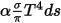
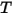 ) und den Emissionseigenschaften des Strahls. Aus dem Stefan-Boltzmann-Gesetz und der Reziprozität von Emission und Absorption, Gleichung 2.274 und Gleichung 2.279, ergibt sich für die vom Medium emittierte Strahlung:
) und den Emissionseigenschaften des Strahls. Aus dem Stefan-Boltzmann-Gesetz und der Reziprozität von Emission und Absorption, Gleichung 2.274 und Gleichung 2.279, ergibt sich für die vom Medium emittierte Strahlung: 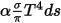
Wenn ferner davon ausgegangen wird, dass n der Brechungsindex des Mediums ist (definiert als das Verhältnis der Lichtgeschwindigkeit im Vakuum zur Lichtgeschwindigkeit im angegebenen Medium), ist die tatsächliche Energie, die der Strahlungsstrahl gewinnt, die folgende:
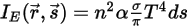
Gleichung 2.284
• Streuung sonstiger Strahlung – Ein Anteil sonstiger Strahlungsquellen in der Schicht des Mediums wird hin zum Strahl gestreut, abhängig von den Positions- und Richtungsvektoren 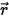 und
und 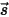 . Wenn
. Wenn 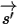
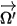 eingeführt wird, um die Richtung und den Raumwinkel des Strahlungsstrahls darzustellen, und wenn
eingeführt wird, um die Richtung und den Raumwinkel des Strahlungsstrahls darzustellen, und wenn 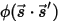 die Phasenfunktion ist, wird der Anteil der Intensität eines Strahls, der in alle Richtungen geht, um in die Richtung
die Phasenfunktion ist, wird der Anteil der Intensität eines Strahls, der in alle Richtungen geht, um in die Richtung 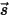 ⃗gestreut zu werden, folgendermaßen ermittelt:
⃗gestreut zu werden, folgendermaßen ermittelt:
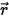 und
und 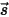 . Wenn
. Wenn 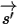
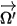 eingeführt wird, um die Richtung und den Raumwinkel des Strahlungsstrahls darzustellen, und wenn
eingeführt wird, um die Richtung und den Raumwinkel des Strahlungsstrahls darzustellen, und wenn 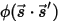 die Phasenfunktion ist, wird der Anteil der Intensität eines Strahls, der in alle Richtungen geht, um in die Richtung
die Phasenfunktion ist, wird der Anteil der Intensität eines Strahls, der in alle Richtungen geht, um in die Richtung 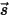 ⃗gestreut zu werden, folgendermaßen ermittelt:
⃗gestreut zu werden, folgendermaßen ermittelt: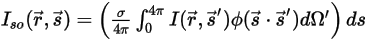
Gleichung 2.285
Beachten Sie, dass die Streuungsprozesse in Gleichung 2.285 ignoriert werden.
Bei eingehender Strahlung 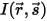 und ausgehender Strahlung
und ausgehender Strahlung 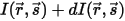 lässt sich die Strahlungsenergiebilanz in Richtung
lässt sich die Strahlungsenergiebilanz in Richtung 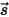 ⃗ in der folgenden Formel ausdrücken:
⃗ in der folgenden Formel ausdrücken:
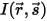 und ausgehender Strahlung
und ausgehender Strahlung 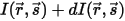 lässt sich die Strahlungsenergiebilanz in Richtung
lässt sich die Strahlungsenergiebilanz in Richtung 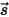 ⃗ in der folgenden Formel ausdrücken:
⃗ in der folgenden Formel ausdrücken: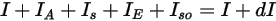
Gleichung 2.286
Durch Substitution von Gleichung 2.282 bis Gleichung 2.285 in Gleichung 2.286 und Division durch 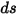 ergibt sich folgende Strahlungstransportgleichung (RTE):
ergibt sich folgende Strahlungstransportgleichung (RTE):
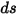 ergibt sich folgende Strahlungstransportgleichung (RTE):
ergibt sich folgende Strahlungstransportgleichung (RTE):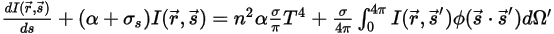
Gleichung 2.287
Die Strahlungstransportgleichung ist eine Integro-Differentialgleichung erster Ordnung für die Strahlungsintensität 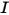 in einer festen Richtung
in einer festen Richtung 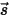 . Um diese Gleichung innerhalb einer Domäne zu lösen, benötigen Sie das Temperaturfeld innerhalb der Domäne sowie darüber hinaus die Randbedingungen für
. Um diese Gleichung innerhalb einer Domäne zu lösen, benötigen Sie das Temperaturfeld innerhalb der Domäne sowie darüber hinaus die Randbedingungen für 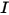 auf den internen und den externen Fläche, ebenso wie die Grenzflächen zwischen zwei verschiedenen Medien.
auf den internen und den externen Fläche, ebenso wie die Grenzflächen zwischen zwei verschiedenen Medien.
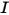 in einer festen Richtung
in einer festen Richtung 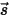 . Um diese Gleichung innerhalb einer Domäne zu lösen, benötigen Sie das Temperaturfeld innerhalb der Domäne sowie darüber hinaus die Randbedingungen für
. Um diese Gleichung innerhalb einer Domäne zu lösen, benötigen Sie das Temperaturfeld innerhalb der Domäne sowie darüber hinaus die Randbedingungen für 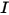 auf den internen und den externen Fläche, ebenso wie die Grenzflächen zwischen zwei verschiedenen Medien.
auf den internen und den externen Fläche, ebenso wie die Grenzflächen zwischen zwei verschiedenen Medien.Die lokale Mediumtemperatur wird durch Lösen der im Modul Heat beschriebenen Gesamtenergie-Erhaltungsgleichung (einschließlich der Strahlungsquellen) ermittelt. Für die Wärmestrahlung ist die Behandlung der Berandungen jedoch komplex und hängt von den Strahlungsmodellen ab. Im Allgemeinen kann eine Berandung ein undurchsichtiges Medium sein, das emittiert, reflektiert und absorbiert, oder ein semi-transparentes Medium, das auch transmittiert. Reflexion und Transmission können diffus oder gerichtet oder sowohl diffus als auch gerichtet sein. Beispielsweise kann bei einer emittierenden und reflektierenden undurchsichtigen Berandung mit grauer Strahlung und je nach Art der Reflexion die Intensität eines Strahls wie folgt ausgedrückt werden:
◦ Undurchsichtige Berandung mit diffuser Emission und Reflexion:
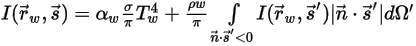
Gleichung 2.288
◦ Undurchsichtige Berandung mit diffuser Emission und Spiegelreflexion:
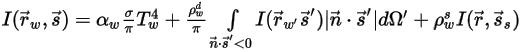
Gleichung 2.289
Dabei gilt:
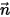 ⃗ ⃗ | Einheitsvektor senkrecht zur Fläche an Position 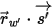 |
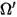 | Richtung und Raumwinkel eines diffus reflektierten Strahls (gleichmäßige Reflexion in alle Richtungen) |
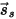 | Richtung des gerichtet reflektierten Strahls (perfekte Reflexion je nach Inzidenz) |
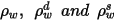 | Flächenreflexion, diffuse Reflexion und gerichtete Reflexion, die in folgender Beziehung stehen: 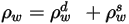 Gleichung 2.290 |
Mit den angegebenen Randbedingungen bestimmt die Gleichung 2.287 den Transport der Strahlungsintensität in einer bestimmten Richtung. Für graue Strahlungen sollte die Gleichung 2.287 in allen verschiedenen Richtungen innerhalb einer Kugel gelöst werden. Für nicht-graue Strahlungen hängt die Intensität auch von den Wellenlängen ab. Daher muss sie in allen Richtungen über das gesamte Spektrum der Wellenlängen hinweg gelöst werden. Natürlich ist die direkte Lösung der Strahlungstransportgleichung sehr zeitaufwendig. In vielen technischen Simulationen ist es daher wünschenswert, etwas vereinfachte, aber annähernde Modelle zu verwenden, um die direktionalen und spektralen Abhängigkeiten zu berücksichtigen. In CFD-Simulationen werden die folgenden Strahlungsmodelle routinemäßig übernommen, die in den Referenzen detailliert beschrieben sind.
Referenzen: R. Siegel und J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Rosseland-Strahlungsmodell
Referenzen: R. Siegel und J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ P-1-Strahlungsmodell
Referenzen: R. Siegel und J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Diskreter-Transfer-Strahlungsmodell
Referenzen: N. G. Shah, "A New Method of Computation of Radiant Heat Transfer in Combustion Chambers", PhD thesis, Imperial College of Science and Technology, London, England, 1979.
Referenzen: M. G. Carvalho, T. Farias und P. Fontes, "Predicting Radiative Heat Transfer in Absorbing, Emitting, and Scattering Media Using the Discrete Transfer Method", In W. A. Fiveland et al., editor, Fundamentals of Radiation Heat Transfer, Volume 160, Seite 17-26. ASME HTD, 1991.
▪ Surface-to-Surface-Strahlungsmodell (S2S)
Referenzen: R. Siegel und J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Diskrete-Ordinaten-Strahlungsmodell (DO)
Referenzen: G. D. Raithby und E. H. Chui, "A Finite-Volume Method for Predicting a Radiant Heat Transfer in Enclosures with Participating Media", J. Heat Transfer, 112:415-423, 1990.
Referenzen: E. H. Chui und G. D. Raithby, "Computation of Radiant Heat Transfer on a Non-Orthogonal Mesh Using the Finite-Volume Method", Numerical Heat Transfer, Teil B, 23:269-288, 1993.
Jedes Modell hat seine eigenen Vorteile und Einschränkungen hinsichtlich Genauigkeit und Kosten. Während das Rosseland-Modell beispielsweise keine Transportgleichung für die auftreffende Strahlung löst, ist es das schnellste Strahlungsmodell und erfordert den geringsten zusätzlichen Speicherplatz. Rosseland kann aufgrund seiner starken Vereinfachung der Strahlungstransportgleichung nur für optisch dicke Medien verwendet werden. (Die optische Dicke ist der natürliche Logarithmus des Verhältnisses zwischen auftreffender und transmittierter Strahlungsleistung in einem Medium.)
Das Strahlungsmodell mit diskreten Ordinaten (DO) wandelt die Gleichung 2.287 in eine Transportgleichung für die Strahlungsintensität in den Raumkoordinaten 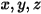 um und löst diese über eine finite Anzahl diskreter Raumwinkel, die der Vektorrichtung
um und löst diese über eine finite Anzahl diskreter Raumwinkel, die der Vektorrichtung 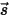 zugeordnet sind. Die Anzahl der ausgewählten Raumwinkel bestimmt direkt die Genauigkeit und die Rechenkosten. Der DO-Modellierungsansatz ist auch mit dem für die Flüssigkeitsfluss- und Energiegleichungen verwendeten Ansatz identisch. Derzeit ist dies das allgemeinste Strahlungsmodell, das sich auf die gesamte Bandbreite optischer Dicken erstreckt und auf Probleme von der Surface-to-Surface-Strahlung bis hin zur beteiligten Strahlung, z.B. bei einem Verbrennungssystem, angewendet werden kann. Die Rechenkosten des DO-Modells sind für nicht-graue Strahlungen hoch.
zugeordnet sind. Die Anzahl der ausgewählten Raumwinkel bestimmt direkt die Genauigkeit und die Rechenkosten. Der DO-Modellierungsansatz ist auch mit dem für die Flüssigkeitsfluss- und Energiegleichungen verwendeten Ansatz identisch. Derzeit ist dies das allgemeinste Strahlungsmodell, das sich auf die gesamte Bandbreite optischer Dicken erstreckt und auf Probleme von der Surface-to-Surface-Strahlung bis hin zur beteiligten Strahlung, z.B. bei einem Verbrennungssystem, angewendet werden kann. Die Rechenkosten des DO-Modells sind für nicht-graue Strahlungen hoch.
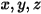 um und löst diese über eine finite Anzahl diskreter Raumwinkel, die der Vektorrichtung
um und löst diese über eine finite Anzahl diskreter Raumwinkel, die der Vektorrichtung 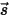 zugeordnet sind. Die Anzahl der ausgewählten Raumwinkel bestimmt direkt die Genauigkeit und die Rechenkosten. Der DO-Modellierungsansatz ist auch mit dem für die Flüssigkeitsfluss- und Energiegleichungen verwendeten Ansatz identisch. Derzeit ist dies das allgemeinste Strahlungsmodell, das sich auf die gesamte Bandbreite optischer Dicken erstreckt und auf Probleme von der Surface-to-Surface-Strahlung bis hin zur beteiligten Strahlung, z.B. bei einem Verbrennungssystem, angewendet werden kann. Die Rechenkosten des DO-Modells sind für nicht-graue Strahlungen hoch.
zugeordnet sind. Die Anzahl der ausgewählten Raumwinkel bestimmt direkt die Genauigkeit und die Rechenkosten. Der DO-Modellierungsansatz ist auch mit dem für die Flüssigkeitsfluss- und Energiegleichungen verwendeten Ansatz identisch. Derzeit ist dies das allgemeinste Strahlungsmodell, das sich auf die gesamte Bandbreite optischer Dicken erstreckt und auf Probleme von der Surface-to-Surface-Strahlung bis hin zur beteiligten Strahlung, z.B. bei einem Verbrennungssystem, angewendet werden kann. Die Rechenkosten des DO-Modells sind für nicht-graue Strahlungen hoch.Unter den oben genannten Strahlungsmodellen eignet sich das Surface-to-Surface-Strahlungsmodell (S2S) besonders gut für die Modellierung des Strahlungstransports im geschlossenen Raum ohne Berücksichtigung der beteiligten Medien. Typische Beispiele sind Strahlungsheizkörper sowie Motorraum- und Unterbodensysteme für Kraftfahrzeuge. In diesen Situationen sind die Strahlungsmodelle für die beteiligte Strahlung manchmal nicht effizient. Im Vergleich zum DO-Strahlungsmodell ist das S2S-Modell pro Iteration viel schneller, obwohl die Berechnung des Ansichtsfaktors selbst CPU-intensiv sein kann. In Creo Flow Analysis ist aktuell als Modell für die Strahlungswärmeübertragung das S2S-Strahlungsmodell ausgewählt.
Surface-to-Surface-Strahlungsmodell (S2S)
Das Surface-to-Surface-Strahlungsmodell berücksichtigt den Strahlungsaustausch in einem geschlossenen Raum mit grauen, diffusen Flächen ohne beteiligte Medien. Der Surface-to-Surface-Strahlungsenergieaustausch hängt von zwei Hauptfaktoren ab: den Strahlungseigenschaften der beteiligten Flächen und den geometrischen Parametern, einschließlich der Flächenbereiche und Formen, und der relativen Position, um einander zu erreichen (Trennabstand und Orientierung). Im S2S-Strahlungsmodell wird die Flächen-Strahlungswärmeübertragung vom grau-diffusen Strahlungsmodell berücksichtigt, während die geometrischen Parameter von einer geometrischen Funktion berücksichtigt werden, die als Ansichtsfaktor bezeichnet wird.
• Grau-diffuse Strahlung
Beim S2S-Strahlungsmodell wird angenommen, dass die Flächen grau und diffus sind (graue Strahlung). Bei einer grauen Fläche sind sowohl Emissionsgrad 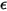 als auch Absorptionsgrad
als auch Absorptionsgrad 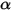 der Flächen unabhängig von der Wellenlänge der ausgehenden und eingehenden Strahlen. Gemäß dem Kirchhoff-Gesetz der Wärmestrahlung ist in Gleichung 2.274 der Emissionsgrad gleich dem Absorptionsgrad:
der Flächen unabhängig von der Wellenlänge der ausgehenden und eingehenden Strahlen. Gemäß dem Kirchhoff-Gesetz der Wärmestrahlung ist in Gleichung 2.274 der Emissionsgrad gleich dem Absorptionsgrad:
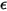 als auch Absorptionsgrad
als auch Absorptionsgrad 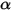 der Flächen unabhängig von der Wellenlänge der ausgehenden und eingehenden Strahlen. Gemäß dem Kirchhoff-Gesetz der Wärmestrahlung ist in Gleichung 2.274 der Emissionsgrad gleich dem Absorptionsgrad:
der Flächen unabhängig von der Wellenlänge der ausgehenden und eingehenden Strahlen. Gemäß dem Kirchhoff-Gesetz der Wärmestrahlung ist in Gleichung 2.274 der Emissionsgrad gleich dem Absorptionsgrad: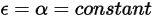
Gleichung 2.291
Ferner kommt es bei der Annahme einer diffusen Fläche zu keiner Spiegelreflexion auf die Fläche und das Reflexionsvermögen (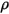 ) der auftreffenden Strahlung an der Fläche ist isotrop bezüglich des Raumwinkels. Aus der Gleichung 2.290 wird das Flächenreflexionsvermögen wie folgt bestimmt:
) der auftreffenden Strahlung an der Fläche ist isotrop bezüglich des Raumwinkels. Aus der Gleichung 2.290 wird das Flächenreflexionsvermögen wie folgt bestimmt:
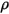 ) der auftreffenden Strahlung an der Fläche ist isotrop bezüglich des Raumwinkels. Aus der Gleichung 2.290 wird das Flächenreflexionsvermögen wie folgt bestimmt:
) der auftreffenden Strahlung an der Fläche ist isotrop bezüglich des Raumwinkels. Aus der Gleichung 2.290 wird das Flächenreflexionsvermögen wie folgt bestimmt: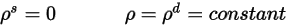
Gleichung 2.292
Dabei gilt:
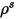 | Flächen gerichtet |
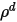 | diffuses Reflexionsvermögen |
Bei einer nicht-undurchsichtigen oder halbtransparenten Fläche ist auch die Transmissivität 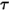 unabhängig von den Wellenlängen:
unabhängig von den Wellenlängen:
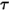 unabhängig von den Wellenlängen:
unabhängig von den Wellenlängen: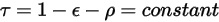
Gleichung 2.293
Beim grau-diffusen Surface-to-Surface-Modell wird angenommen, dass der Austausch von Strahlungsenergie zwischen Flächen durch das Medium, das sie trennt, praktisch nicht beeinflusst wird. Wenn also eine bestimmte Menge Strahlungsenergie 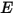 auf eine Fläche pro Flächeneinheit (Bestrahlungsstärke) auftrifft, sind die Teile der Strahlungsenergie, die reflektiert, absorbiert und transmittiert werden,
auf eine Fläche pro Flächeneinheit (Bestrahlungsstärke) auftrifft, sind die Teile der Strahlungsenergie, die reflektiert, absorbiert und transmittiert werden, 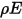 ,
, 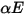 bzw.
bzw. 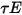 . Da für die meisten Anwendungen die Flächen für Wärmestrahlung im Infrarotspektrum undurchsichtig sind, können die Strahlungsflächen weiterhin als undurchsichtig betrachtet werden. Die Transmissivität kann daher vernachlässigt werden
. Da für die meisten Anwendungen die Flächen für Wärmestrahlung im Infrarotspektrum undurchsichtig sind, können die Strahlungsflächen weiterhin als undurchsichtig betrachtet werden. Die Transmissivität kann daher vernachlässigt werden 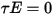 . Aus Gleichung 2.273 und Gleichung 2.274 wird das Flächenreflexionsvermögen
. Aus Gleichung 2.273 und Gleichung 2.274 wird das Flächenreflexionsvermögen 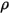 ausgedrückt als:
ausgedrückt als:
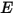 auf eine Fläche pro Flächeneinheit (Bestrahlungsstärke) auftrifft, sind die Teile der Strahlungsenergie, die reflektiert, absorbiert und transmittiert werden,
auf eine Fläche pro Flächeneinheit (Bestrahlungsstärke) auftrifft, sind die Teile der Strahlungsenergie, die reflektiert, absorbiert und transmittiert werden, 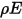 ,
, 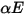 bzw.
bzw. 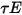 . Da für die meisten Anwendungen die Flächen für Wärmestrahlung im Infrarotspektrum undurchsichtig sind, können die Strahlungsflächen weiterhin als undurchsichtig betrachtet werden. Die Transmissivität kann daher vernachlässigt werden
. Da für die meisten Anwendungen die Flächen für Wärmestrahlung im Infrarotspektrum undurchsichtig sind, können die Strahlungsflächen weiterhin als undurchsichtig betrachtet werden. Die Transmissivität kann daher vernachlässigt werden 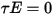 . Aus Gleichung 2.273 und Gleichung 2.274 wird das Flächenreflexionsvermögen
. Aus Gleichung 2.273 und Gleichung 2.274 wird das Flächenreflexionsvermögen 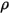 ausgedrückt als:
ausgedrückt als: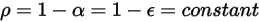
Gleichung 2.294
Unter den Annahmen einer grau-diffusen Strahlung der Flächen wird die S2S-Modellierungsgleichung auf der Basis der Energieerhaltung auf jeder Fläche aufgebaut.
• S2S-Modellierungsgleichung
Die Hauptannahme des S2S-Modells besteht darin, dass in einem geschlossenen System die Strahlungswärmeübertragung nur zwischen grau-diffusen Flächen (graue Strahlung) stattfindet. Die Absorption, Emission oder Streuung von Strahlung im Medium, das die Flächen trennt, kann ignoriert werden. Es wird daher für die numerische Analyse nur die Surface-to-Surface-Strahlung berücksichtigt.
Der Strahlungsenergiefluss, der eine gegebene Fläche verlässt, besteht aus direkt emittierter und reflektierter Energie. Der reflektierte Energiefluss ist abhängig vom auftreffenden Energiefluss aus der Umgebung, der dann in Bezug auf den Energiefluss ausgedrückt werden kann, der alle anderen Flächen verlässt. Um den Strahlungsenergiefluss in einer Fläche zu berechnen, ist es empfehlenswert, die effektive Strahlung 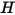 zu definieren, die die Summe der emittierten Leistung pro Flächeneinheit (Emittanz)
zu definieren, die die Summe der emittierten Leistung pro Flächeneinheit (Emittanz) 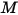 und des reflektierten Teils der Strahlungsleistung ist, die von der Fläche pro Flächeneinheit (Bestrahlungsstärke)
und des reflektierten Teils der Strahlungsleistung ist, die von der Fläche pro Flächeneinheit (Bestrahlungsstärke) 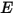 empfangen wird:
empfangen wird:
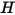 zu definieren, die die Summe der emittierten Leistung pro Flächeneinheit (Emittanz)
zu definieren, die die Summe der emittierten Leistung pro Flächeneinheit (Emittanz) 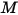 und des reflektierten Teils der Strahlungsleistung ist, die von der Fläche pro Flächeneinheit (Bestrahlungsstärke)
und des reflektierten Teils der Strahlungsleistung ist, die von der Fläche pro Flächeneinheit (Bestrahlungsstärke) 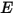 empfangen wird:
empfangen wird: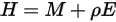
Gleichung 2.295
Bei einer undurchsichtigen Fläche 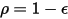 ist folgende effektive Strahlung vorhanden:
ist folgende effektive Strahlung vorhanden:
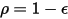 ist folgende effektive Strahlung vorhanden:
ist folgende effektive Strahlung vorhanden: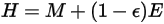
Gleichung 2.296
Unter den Annahmen im S2S-Modell kann daher das folgende System linearer Gleichungen formuliert werden, um die effektive Strahlung auf jeder Fläche in einem geschlossenen System zu berechnen. Unter der Annahme, dass 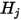 die effektive Strahlung auf einer willkürlichen Fläche
die effektive Strahlung auf einer willkürlichen Fläche 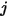 darstellt,
darstellt, 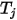 die Oberflächentemperatur ist und
die Oberflächentemperatur ist und 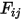 der Ansichtsfaktor zwischen Fläche
der Ansichtsfaktor zwischen Fläche 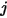 und
und  ist, ergibt sich folgende effektive Strahlung in der Fläche
ist, ergibt sich folgende effektive Strahlung in der Fläche  :
:
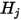 die effektive Strahlung auf einer willkürlichen Fläche
die effektive Strahlung auf einer willkürlichen Fläche 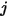 darstellt,
darstellt, 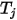 die Oberflächentemperatur ist und
die Oberflächentemperatur ist und 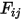 der Ansichtsfaktor zwischen Fläche
der Ansichtsfaktor zwischen Fläche 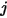 und
und  ist, ergibt sich folgende effektive Strahlung in der Fläche
ist, ergibt sich folgende effektive Strahlung in der Fläche  :
: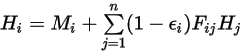
Gleichung 2.297
Dabei ist 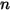 die Anzahl der Flächen, die an der Strahlungswärmeübertragung beteiligt sind. Durch Einführung des Kronecker-Symbols
die Anzahl der Flächen, die an der Strahlungswärmeübertragung beteiligt sind. Durch Einführung des Kronecker-Symbols 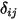 und Anwendung des Stefan-Boltzmann-Gesetzes für graue Strahlung, Gleichung 2.278, können Sie die Gleichung 2.297 umformen und die S2S-Modellierungsgleichung ableiten:
und Anwendung des Stefan-Boltzmann-Gesetzes für graue Strahlung, Gleichung 2.278, können Sie die Gleichung 2.297 umformen und die S2S-Modellierungsgleichung ableiten:
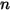 die Anzahl der Flächen, die an der Strahlungswärmeübertragung beteiligt sind. Durch Einführung des Kronecker-Symbols
die Anzahl der Flächen, die an der Strahlungswärmeübertragung beteiligt sind. Durch Einführung des Kronecker-Symbols 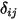 und Anwendung des Stefan-Boltzmann-Gesetzes für graue Strahlung, Gleichung 2.278, können Sie die Gleichung 2.297 umformen und die S2S-Modellierungsgleichung ableiten:
und Anwendung des Stefan-Boltzmann-Gesetzes für graue Strahlung, Gleichung 2.278, können Sie die Gleichung 2.297 umformen und die S2S-Modellierungsgleichung ableiten: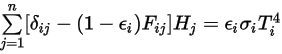
Gleichung 2.298
Mit dem zuvor berechneten Ansichtsfaktor 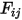 wird das System der linearen Gleichung 2.298 gelöst, um
wird das System der linearen Gleichung 2.298 gelöst, um 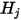 für die beteiligten Flächen zu erhalten. Anschließend lassen sich die Netto-Strahlungswärmeflüsse auf jeder Fläche leicht berechnen. Für die Fläche
für die beteiligten Flächen zu erhalten. Anschließend lassen sich die Netto-Strahlungswärmeflüsse auf jeder Fläche leicht berechnen. Für die Fläche  ist der Netto-Strahlungswärmefluss
ist der Netto-Strahlungswärmefluss 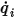 der Unterschied zwischen der ausgehenden (
der Unterschied zwischen der ausgehenden (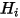 ) und der eingehenden (
) und der eingehenden (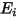 ) Strahlung pro Flächeneinheit. Aus der Gleichung 2.278 und der Gleichung 2.296 können Sie die folgende Fluss-Formel ableiten:
) Strahlung pro Flächeneinheit. Aus der Gleichung 2.278 und der Gleichung 2.296 können Sie die folgende Fluss-Formel ableiten:
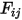 wird das System der linearen Gleichung 2.298 gelöst, um
wird das System der linearen Gleichung 2.298 gelöst, um 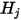 für die beteiligten Flächen zu erhalten. Anschließend lassen sich die Netto-Strahlungswärmeflüsse auf jeder Fläche leicht berechnen. Für die Fläche
für die beteiligten Flächen zu erhalten. Anschließend lassen sich die Netto-Strahlungswärmeflüsse auf jeder Fläche leicht berechnen. Für die Fläche  ist der Netto-Strahlungswärmefluss
ist der Netto-Strahlungswärmefluss 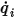 der Unterschied zwischen der ausgehenden (
der Unterschied zwischen der ausgehenden (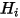 ) und der eingehenden (
) und der eingehenden (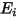 ) Strahlung pro Flächeneinheit. Aus der Gleichung 2.278 und der Gleichung 2.296 können Sie die folgende Fluss-Formel ableiten:
) Strahlung pro Flächeneinheit. Aus der Gleichung 2.278 und der Gleichung 2.296 können Sie die folgende Fluss-Formel ableiten: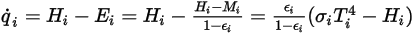
Gleichung 2.299
Für einen gegebenen Flächeninhalt 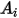 werden die Strahlungswärmeflüsse, die die Fläche
werden die Strahlungswärmeflüsse, die die Fläche 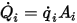 verlassen, wie folgt berechnet:
verlassen, wie folgt berechnet:
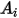 werden die Strahlungswärmeflüsse, die die Fläche
werden die Strahlungswärmeflüsse, die die Fläche 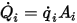 verlassen, wie folgt berechnet:
verlassen, wie folgt berechnet: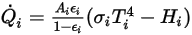
Gleichung 2.300
Das S2S-Modell besteht aus einem System linearer Gleichungen in der Form der Gleichung 2.298. Der Vorteil bei der Anwendung des Modells besteht darin, dass Sie für gegebene Ansichtsfaktoren und Temperaturen die Netto-Wärmeflüsse durch Lösen eines Systems linearer Gleichungen berechnen können, die durch Anwenden numerischer Algorithmen berechnet werden. Die Hauptschwierigkeit bei der Anwendung des vorgeschlagenen Surface-to-Surface-Modells ist jedoch die Berechnung der Ansichtsfaktoren 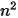 für die Anzahl n der beteiligten Flächen. Es kann sehr zeitaufwendig sein, insbesondere mit zunehmender Anzahl von Flächen.
für die Anzahl n der beteiligten Flächen. Es kann sehr zeitaufwendig sein, insbesondere mit zunehmender Anzahl von Flächen.
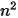 für die Anzahl n der beteiligten Flächen. Es kann sehr zeitaufwendig sein, insbesondere mit zunehmender Anzahl von Flächen.
für die Anzahl n der beteiligten Flächen. Es kann sehr zeitaufwendig sein, insbesondere mit zunehmender Anzahl von Flächen.Berechnung des Ansichtsfaktors
In der S2S-Modellierungsgleichung 2.298 ist der Ansichtsfaktor 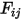 der Anteil der Strahlung, der die Fläche
der Anteil der Strahlung, der die Fläche  verlässt und auf die Fläche
verlässt und auf die Fläche 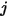 auftrifft. Wie in Abbildung 2.37 dargestellt, wird unter der Annahme, dass
auftrifft. Wie in Abbildung 2.37 dargestellt, wird unter der Annahme, dass 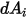 die Differenzfläche auf der Fläche
die Differenzfläche auf der Fläche  und
und 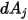 die Differenzfläche auf der Fläche
die Differenzfläche auf der Fläche 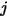 und der Abstand zwischen
und der Abstand zwischen 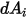 und
und 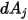
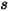 ist, der Ansichtsfaktor
ist, der Ansichtsfaktor 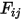 von
von 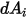 bis
bis 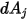 in einem Abstand
in einem Abstand 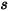 wie folgt ausgedrückt:
wie folgt ausgedrückt:
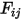 der Anteil der Strahlung, der die Fläche
der Anteil der Strahlung, der die Fläche  verlässt und auf die Fläche
verlässt und auf die Fläche 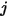 auftrifft. Wie in Abbildung 2.37 dargestellt, wird unter der Annahme, dass
auftrifft. Wie in Abbildung 2.37 dargestellt, wird unter der Annahme, dass 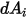 die Differenzfläche auf der Fläche
die Differenzfläche auf der Fläche  und
und 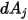 die Differenzfläche auf der Fläche
die Differenzfläche auf der Fläche 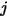 und der Abstand zwischen
und der Abstand zwischen 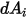 und
und 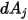
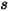 ist, der Ansichtsfaktor
ist, der Ansichtsfaktor 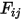 von
von 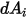 bis
bis 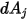 in einem Abstand
in einem Abstand 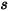 wie folgt ausgedrückt:
wie folgt ausgedrückt: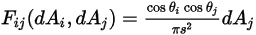
Gleichung 2.301
Dabei sind 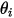 und
und 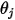 der Winkel zwischen den Flächennormalenrichtungen und einem Strahl zwischen den beiden Differenzflächen.
der Winkel zwischen den Flächennormalenrichtungen und einem Strahl zwischen den beiden Differenzflächen.
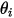 und
und 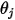 der Winkel zwischen den Flächennormalenrichtungen und einem Strahl zwischen den beiden Differenzflächen.
der Winkel zwischen den Flächennormalenrichtungen und einem Strahl zwischen den beiden Differenzflächen.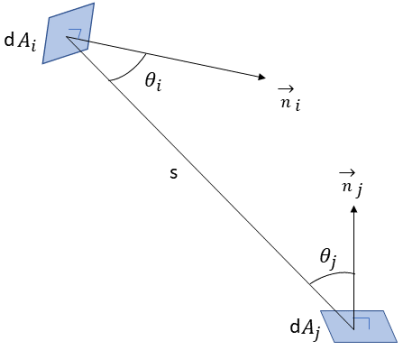
Abbildung 2.37
Wenn 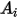 und
und 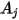 die gegebenen Bereiche der Flächen
die gegebenen Bereiche der Flächen  bzw.
bzw. 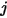 sind, dann ist der Ansichtsfaktor von Fläche
sind, dann ist der Ansichtsfaktor von Fläche  zu Fläche
zu Fläche 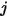 das flächengemittelte Integral von Gleichung 2.301 über die Flächen
das flächengemittelte Integral von Gleichung 2.301 über die Flächen  und
und 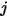 :
:
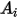 und
und 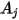 die gegebenen Bereiche der Flächen
die gegebenen Bereiche der Flächen  bzw.
bzw. 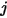 sind, dann ist der Ansichtsfaktor von Fläche
sind, dann ist der Ansichtsfaktor von Fläche  zu Fläche
zu Fläche 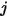 das flächengemittelte Integral von Gleichung 2.301 über die Flächen
das flächengemittelte Integral von Gleichung 2.301 über die Flächen  und
und 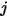 :
: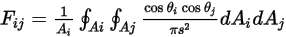
Gleichung 2.302
Beachten Sie, dass Surface-to-Surface-Strahlung nur dann auftritt, wenn die beiden Flächen sichtbar für einander sind oder der Ansichtsfaktor nicht 0 ist. Durch Einführung des Kronecker-Symbols 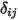 bezüglich der Sichtbarkeit zwischen
bezüglich der Sichtbarkeit zwischen 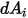 und
und 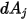 :
:
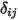 bezüglich der Sichtbarkeit zwischen
bezüglich der Sichtbarkeit zwischen 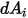 und
und 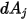 :
: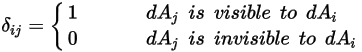
Gleichung 2.303
können Sie die Gleichung 2.302 umformulieren in:
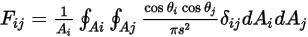
Gleichung 2.304
Bei zwei beliebigen sichtbaren Flächen, die füreinander sichtbar sind, strahlt eine gegebene Fläche  nur einen Teil der ausgehenden Strahlungsenergie an die Fläche
nur einen Teil der ausgehenden Strahlungsenergie an die Fläche 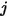 aus, wie in Abbildung 2.378 gezeigt. Daher stellt der dimensionslose Ansichtsfaktor
aus, wie in Abbildung 2.378 gezeigt. Daher stellt der dimensionslose Ansichtsfaktor 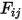 den Teil der Energie dar, der die Fläche
den Teil der Energie dar, der die Fläche  verlässt und die Fläche
verlässt und die Fläche 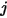 erreicht. Die Merkmale sind in der folgenden Liste aufgeführt:
erreicht. Die Merkmale sind in der folgenden Liste aufgeführt:
 nur einen Teil der ausgehenden Strahlungsenergie an die Fläche
nur einen Teil der ausgehenden Strahlungsenergie an die Fläche 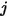 aus, wie in Abbildung 2.378 gezeigt. Daher stellt der dimensionslose Ansichtsfaktor
aus, wie in Abbildung 2.378 gezeigt. Daher stellt der dimensionslose Ansichtsfaktor 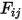 den Teil der Energie dar, der die Fläche
den Teil der Energie dar, der die Fläche  verlässt und die Fläche
verlässt und die Fläche 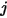 erreicht. Die Merkmale sind in der folgenden Liste aufgeführt:
erreicht. Die Merkmale sind in der folgenden Liste aufgeführt: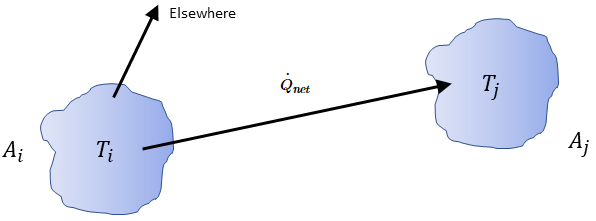
Abbildung 2.378
• Summierung von Ansichtsfaktoren – Da Strahlung, die eine Fläche verlässt, erhalten bleibt, ist die Summe aller Ansichtsfaktoren einer gegebenen Fläche  gleich 1. Für das System eingeschlossener Flächen
gleich 1. Für das System eingeschlossener Flächen 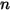 gilt:
gilt:
 gleich 1. Für das System eingeschlossener Flächen
gleich 1. Für das System eingeschlossener Flächen 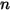 gilt:
gilt:
Gleichung 2.305
• Sich selbst sehende Flächen – Da Strahlung in geraden Linien verläuft, kann kein Strahlungsstrahl von einer konvexen Fläche die Fläche verlassen und dann später wieder auf dieselbe Fläche auftreffen. Daher können die konvexen Flächen sich nicht selbst sehen:
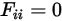
Gleichung 2.306
Bei konkaven Flächen kann der ausgehende Strahl von einer Position auf der Fläche später an einer anderen Position auf dieselbe Fläche auftreffen. Daher kann die konkave Fläche für sich selbst sichtbar sein:
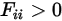
Gleichung 2.307
• Überlagerung – Wenn für ein Flächensystem 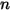 eine gegebene Fläche
eine gegebene Fläche  auf die Anzahl
auf die Anzahl 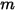 von Flächen (
von Flächen (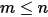 ) ausstrahlt, entspricht der Ansichtsfaktor zwischen der Fläche
) ausstrahlt, entspricht der Ansichtsfaktor zwischen der Fläche  und der Anzahl
und der Anzahl 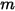 von Flächen der Summe der Ansichtsfaktoren zwischen der Fläche
von Flächen der Summe der Ansichtsfaktoren zwischen der Fläche  und jeder der Anzahl
und jeder der Anzahl 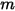 von Flächen:
von Flächen:
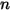 eine gegebene Fläche
eine gegebene Fläche  auf die Anzahl
auf die Anzahl 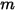 von Flächen (
von Flächen (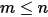 ) ausstrahlt, entspricht der Ansichtsfaktor zwischen der Fläche
) ausstrahlt, entspricht der Ansichtsfaktor zwischen der Fläche  und der Anzahl
und der Anzahl 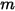 von Flächen der Summe der Ansichtsfaktoren zwischen der Fläche
von Flächen der Summe der Ansichtsfaktoren zwischen der Fläche  und jeder der Anzahl
und jeder der Anzahl 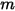 von Flächen:
von Flächen: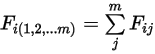
Gleichung 2.308
Die Überlagerungsregel oder Summierungsregel ist nützlich, wenn eine Geometrie mit den gegebenen Diagrammen oder Graphen nicht verfügbar ist. Mit der Überlagerungsregel können Sie die gesuchte Geometrie unter Verwendung der Summe oder Differenz der bekannten Geometrien ausdrücken.
• Reziprozität – Gleichung 2.304 definiert den Ansichtsfaktor 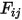 als Anteil der Strahlungsenergie, die die Fläche
als Anteil der Strahlungsenergie, die die Fläche  verlässt und die Fläche
verlässt und die Fläche 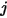 erreicht. Ebenso wird der Ansichtsfaktor
erreicht. Ebenso wird der Ansichtsfaktor 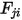 , der der Teil der Energie ist, der die Fläche
, der der Teil der Energie ist, der die Fläche 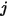 verlässt und die Fläche
verlässt und die Fläche  erreicht, ausgedrückt als:
erreicht, ausgedrückt als:
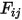 als Anteil der Strahlungsenergie, die die Fläche
als Anteil der Strahlungsenergie, die die Fläche  verlässt und die Fläche
verlässt und die Fläche 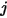 erreicht. Ebenso wird der Ansichtsfaktor
erreicht. Ebenso wird der Ansichtsfaktor 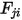 , der der Teil der Energie ist, der die Fläche
, der der Teil der Energie ist, der die Fläche 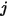 verlässt und die Fläche
verlässt und die Fläche  erreicht, ausgedrückt als:
erreicht, ausgedrückt als: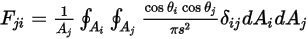
Gleichung 2.309
Wenn Sie die Gleichung 2.309 mit der Gleichung 2.304 vergleichen, erhalten Sie die folgende Beziehung:
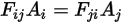
Gleichung 2.310
Gleichung 2.310 wird als die Reziprozität der Ansichtsfaktoren bezeichnet. Mit dem Reziprozitätstheorem können Sie nur einen der Ansichtsfaktoren des Paars direkt berechnen.
Clusterbildung
Das S2S-Strahlungsmodell ist rechnerisch aufwendig, wenn die Anzahl der strahlenden Flächen groß ist. Sie können die Anzahl der strahlenden Flächen reduzieren, um die Rechenzeit und die Speicheranforderung zu reduzieren, indem Sie eine bestimmte Anzahl der benachbarten Berandungszellenflächen gruppieren, um Flächen-Cluster zu erzeugen. Die effektive Strahlung (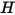 ) wird dann für Flächen-Cluster berechnet. Diese Werte werden dann auf die Berandungszellenflächen in jedem Cluster verteilt, um die Wandtemperaturen zu berechnen. Da die Strahlungsquellenterme in hohem Maße nicht-linear sind (proportional zur vierten Potenz der Temperatur), achten Sie darauf, die Durchschnittstemperatur der Flächen-Cluster zu berechnen und die Fluss- und Quellterme angemessen auf die Berandungsseitenflächen zu verteilen, die die Cluster bilden.
) wird dann für Flächen-Cluster berechnet. Diese Werte werden dann auf die Berandungszellenflächen in jedem Cluster verteilt, um die Wandtemperaturen zu berechnen. Da die Strahlungsquellenterme in hohem Maße nicht-linear sind (proportional zur vierten Potenz der Temperatur), achten Sie darauf, die Durchschnittstemperatur der Flächen-Cluster zu berechnen und die Fluss- und Quellterme angemessen auf die Berandungsseitenflächen zu verteilen, die die Cluster bilden.
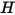 ) wird dann für Flächen-Cluster berechnet. Diese Werte werden dann auf die Berandungszellenflächen in jedem Cluster verteilt, um die Wandtemperaturen zu berechnen. Da die Strahlungsquellenterme in hohem Maße nicht-linear sind (proportional zur vierten Potenz der Temperatur), achten Sie darauf, die Durchschnittstemperatur der Flächen-Cluster zu berechnen und die Fluss- und Quellterme angemessen auf die Berandungsseitenflächen zu verteilen, die die Cluster bilden.
) wird dann für Flächen-Cluster berechnet. Diese Werte werden dann auf die Berandungszellenflächen in jedem Cluster verteilt, um die Wandtemperaturen zu berechnen. Da die Strahlungsquellenterme in hohem Maße nicht-linear sind (proportional zur vierten Potenz der Temperatur), achten Sie darauf, die Durchschnittstemperatur der Flächen-Cluster zu berechnen und die Fluss- und Quellterme angemessen auf die Berandungsseitenflächen zu verteilen, die die Cluster bilden.Die Flächen-Cluster-Temperatur wird durch eine Flächenmittelung der Berandungsseitenflächen-Temperatur ermittelt, wie in der folgenden Gleichung gezeigt:
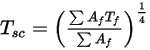
Gleichung 2.311
Dabei ist 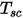 die Temperatur des Flächen-Clusters und
die Temperatur des Flächen-Clusters und 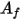 und
und 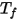 sind der Flächenbereich und die Temperatur der Berandungszelle in CFA-Simulationen. Die Summierung wird über alle Flächen innerhalb eines Flächen-Clusters übertragen.
sind der Flächenbereich und die Temperatur der Berandungszelle in CFA-Simulationen. Die Summierung wird über alle Flächen innerhalb eines Flächen-Clusters übertragen.
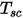 die Temperatur des Flächen-Clusters und
die Temperatur des Flächen-Clusters und 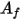 und
und 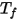 sind der Flächenbereich und die Temperatur der Berandungszelle in CFA-Simulationen. Die Summierung wird über alle Flächen innerhalb eines Flächen-Clusters übertragen.
sind der Flächenbereich und die Temperatur der Berandungszelle in CFA-Simulationen. Die Summierung wird über alle Flächen innerhalb eines Flächen-Clusters übertragen.