Partikel-Erosionsmodellierung
Erosion ist ein Phänomen, das Materialverlust durch wiederholtes Aufprallen von festen Partikeln auf einer Fläche verursacht. Erosion schädigt Rohre, Ventile und andere Durchflüsse. Daher ist es wichtig, die Erosionsrate zu untersuchen und Bereiche in den Durchflüssen zu identifizieren, die anfällig für Erosion sind.
Die CFA-basierte Erosionsmodellierung umfasst die folgenden Schritte:
1. Strömungsfelddaten wie die Geschwindigkeit werden durch Lösen der Navier-Stokes-Gleichungen ermittelt.
2. Partikel werden innerhalb des Strömungsfelds freigesetzt und einzeln verfolgt, um Informationen wie die Aufprallgeschwindigkeit und den Aufprallwinkel zu ermitteln.
3. Die Aufprallinformationen von Partikeln werden in einer Erosionsgleichung verwendet, um das Erosionsverhältnis/die Erosionsrate oder den Flächenmassenverlust durch die aufprallenden Partikel zu berechnen.
Erosionsgleichungen untersuchen die Auswirkungen verschiedener Parameter auf die Erosion, beispielsweise:
Referenzen: Mazdak Parsi et al. "A comprehensive review of solid particle erosion modeling for oil and gas wells and pipelines applications" (2014)
• Partikeleigenschaften wie Größe, Form, Dichte, Härte usw.
• Partikel-Aufprallinformationen wie die Partikel-Aufprallgeschwindigkeit 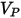 , den Aufprallwinkel
, den Aufprallwinkel 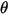 , die Partikel-Partikel-Interaktion usw.
, die Partikel-Partikel-Interaktion usw.
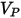 , den Aufprallwinkel
, den Aufprallwinkel 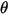 , die Partikel-Partikel-Interaktion usw.
, die Partikel-Partikel-Interaktion usw.• Ziel-Wandeigenschaften wie Materialdichte, Härte usw.
Die Erosionsgleichungen berechnen das Erosionsverhältnis 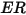 , definiert als die Menge an Wandmaterialverlust (aufgrund des Aufpralls von festen Partikeln) dividiert durch die Masse der aufprallenden festen Partikel.
, definiert als die Menge an Wandmaterialverlust (aufgrund des Aufpralls von festen Partikeln) dividiert durch die Masse der aufprallenden festen Partikel.
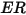 , definiert als die Menge an Wandmaterialverlust (aufgrund des Aufpralls von festen Partikeln) dividiert durch die Masse der aufprallenden festen Partikel.
, definiert als die Menge an Wandmaterialverlust (aufgrund des Aufpralls von festen Partikeln) dividiert durch die Masse der aufprallenden festen Partikel.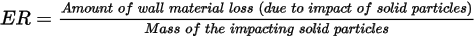
Creo Flow Analysis verwendet die in den folgenden Abschnitten ausführlich beschriebenen Erosionsmodelle:
Referenzen: Mazdak Parsi etc. "CFD simulation of sand particle erosion in gas-dominant multiphase flow" (2015)
Finne-Modell
Die Erosionsgleichung von Finne lautet folgendermaßen:
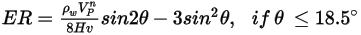
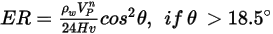
Dabei gilt:
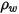 | Wandmaterialdichte (kg/m3) |
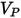 | Partikel-Aufprallgeschwindigkeit (m/s) |
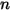 | Geschwindigkeitsexponent (gleich 2 für die meisten industriellen Anwendungen) |
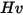 | Vicker-Härte (PA) |
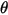 | Aufprallwinkel (Grad) |
Dieses Modell unterschätzt die Materialentfernung für Partikel-Aufprallwinkel größer als 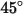 , und für einen normalen Aufprall wird keine Erosion vorausgesagt. , und für einen normalen Aufprall wird keine Erosion vorausgesagt. |
Zhang-Modell
Die Erosionsgleichung von Zhang lautet wie folgt:
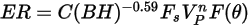
Dabei gilt:
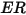 | Erosionsverhältnis |
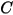 | 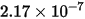 |
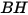 | Brinell-Härte des Wandmaterials (PA) |
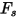 | Partikelformfaktor |
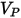 | Partikel-Aufprallgeschwindigkeit (m/s) |
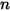 | Geschwindigkeitsexponent (gleich 2,41) |
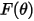 | Aufprallwinkelfunktion |
Der Partikelformfaktor 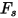 hat die folgenden Werte für verschiedene Typen von Sandpartikeln:
hat die folgenden Werte für verschiedene Typen von Sandpartikeln:
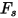 hat die folgenden Werte für verschiedene Typen von Sandpartikeln:
hat die folgenden Werte für verschiedene Typen von Sandpartikeln:Wert | Sandpartikeltyp |
|---|---|
1.0 | spitz oder kantig |
0.53 | halbrund |
0.2 | vollständig gerundet |
Die Aufprallwinkelfunktion wird wie folgt angegeben:
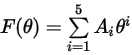
In der folgenden Tabelle sind die Werte von 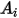 aufgeführt:
aufgeführt:
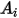 aufgeführt:
aufgeführt: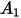 | 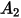 | 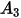 | 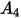 | 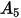 |
|---|---|---|---|---|
5.40 | -10.11 | 10.93 | -6.33 | 1.42 |
Oka-Modell
Die Erosionsgleichung von Oka et al. lautet wie folgt:
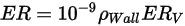
Gleichung 2.406
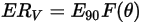
Gleichung 2.407
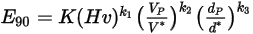
Gleichung 2.408
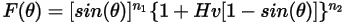
Gleichung 2.409
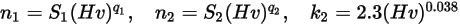
Gleichung 2.410
Dabei gilt:
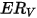 | Volumetrische Erosionsrate (mm3/kg) |
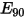 | Erosionsschaden bei einem normalen Aufprallwinkel (mm3/kg) |
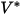 | Referenz-Aufprallgeschwindigkeit (m/s) |
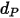 | Partikeldurchmesser (m) |
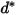 | Referenz-Partikeldurchmesser (m) |
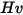 | Vicker-Härte (GPa) |
Die Werte der verschiedenen Koeffizienten, die in Gleichung 2.406, Gleichung 2.407, Gleichung 2.408, Gleichung 2.409 und Gleichung 2.410 verwendet werden, sind in der folgenden Tabelle angegeben:
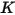 | 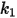 | 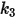 | 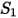 | 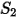 | 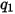 | 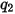 |
|---|---|---|---|---|---|---|
60 | -0.12 | 0.19 | 0.71 | 2.4 | 0.14 | -0.94 |
DNV-Modell
Die Erosionsgleichung von DNV lautet wie folgt:
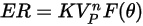
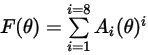
Dabei gilt:
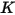 | 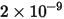 |
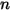 (Geschwindigkeitsexponent) (Geschwindigkeitsexponent) | 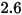 |
In der folgenden Tabelle sind die Werte von 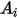 aufgeführt:
aufgeführt:
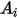 aufgeführt:
aufgeführt: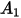 | 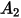 | 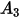 | 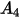 | 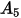 | 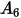 | 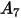 | 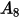 |
|---|---|---|---|---|---|---|---|
9.370 | -42.295 | 110.864 | -175.804 | 170.137 | -98.398 | 31.211 | -4.170 |
Mansouri-Modell
Mansouri hat folgende Erosionsgleichung entwickelt:
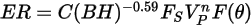
Gleichung 2.413
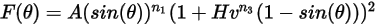
Gleichung 2.414
Dabei gilt:
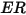 | Erosionsverhältnis |
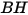 | Brinell-Härte des Wandmaterials (Pa) |
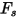 | Partikelformfaktor |
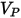 | Partikel-Aufprallgeschwindigkeit (m/s) |
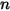 | Geschwindigkeitsexponent |
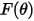 | Aufprallwinkelfunktion |
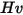 | Vicker-Härte (Pa) |
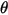 | Aufprallwinkel (Grad) |
In der folgenden Tabelle sind die Werte der verschiedenen Parameter angegeben, die in Gleichung 2.413 und Gleichung 2.414 der Erosionsgleichung von Mansouri (2015) verwendet werden.
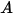 | 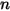 | 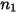 | 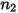 | 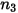 | 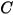 |
|---|---|---|---|---|---|
0.6947 | 2.41 | 0.2 | 0.85 | 0.65 | 4.49e-07 |
Grant-Tabakoff-Modell
Die Erosionsgleichung des Grant-Tabakoff-Modells lautet wie folgt:
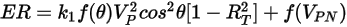
Gleichung 2.415
Dabei gilt:
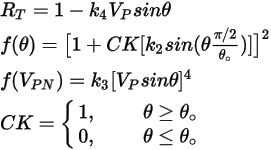
Gleichung 2.416
Dabei gilt:
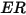 | Erosionsverhältnis |
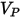 | Partikel-Aufprallgeschwindigkeit (m/s) |
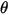 | Aufprallwinkel (Grad) |
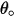 | Winkel der maximalen Erosion (Grad) |
Die Erosionsrate 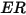 in Gleichung 2.415 ist definiert als die Materialmenge (in Milligramm), die pro Masseneinheit (Gramm) der aufprallenden Partikel entfernt wird. Die Geschwindigkeitseinheit ist ft/s.
in Gleichung 2.415 ist definiert als die Materialmenge (in Milligramm), die pro Masseneinheit (Gramm) der aufprallenden Partikel entfernt wird. Die Geschwindigkeitseinheit ist ft/s.
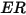 in Gleichung 2.415 ist definiert als die Materialmenge (in Milligramm), die pro Masseneinheit (Gramm) der aufprallenden Partikel entfernt wird. Die Geschwindigkeitseinheit ist ft/s.
in Gleichung 2.415 ist definiert als die Materialmenge (in Milligramm), die pro Masseneinheit (Gramm) der aufprallenden Partikel entfernt wird. Die Geschwindigkeitseinheit ist ft/s.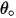 ist der Winkel der maximalen Erosion. Beispiel:
ist der Winkel der maximalen Erosion. Beispiel: 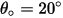 für aluminiumbasierte Legierungen.
für aluminiumbasierte Legierungen.Die Werte der verschiedenen Koeffizienten für das Grant-Tabakoff-Modell sind in der folgenden Tabelle aufgeführt:
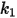 | 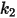 | 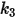 | 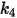 |
3.67e-06 | 0.585 | 6e-12 | 0.0016 |