Diskretes Partikelmodell
Im diskreten Partikelmodell wird die Strömung der dispergierten Phase modelliert, indem eine festgelegte Anzahl von Partikeln durch die kontinuierliche Flüssigkeitsphase verfolgt wird. In Creo Flow Analysis umfasst das Modell die folgenden Annahmen und Einschränkungen:
• Bestimmte Anzahl sphärischer Partikel durch die kontinuierliche Flüssigkeitsflussphase. Die Partikel sind als Mit Masse (Has Mass) oder Masselos (Massless) definiert.
• Ein angegebener Radius bei der Freisetzungsposition und -zeit bestimmt die Größe des Partikels, die unverändert bleibt. Die Partikel-Partikel-Interaktion ist vernachlässigbar.
• Partikel interagieren mit dem Flüssigkeitsstrom und den Wandberandungen. Das Volumen eines Partikels verdrängt keine Flüssigkeit (geringe Volumenanteile in der Partikelphase) bzw. stört nicht die Geometrie. (Ein übergroßes Partikel passt durch einen kleineren Spalt.)
• Zwischen der kontinuierlichen Flüssigkeitsphase und den Partikeln erfolgt keine Wärme- und Massenübertragung. Als Partikeltemperatur wird die lokale Temperatur des Flüssigkeitsstroms angenommen.
Unter diesen Annahmen wird die Bewegung jedes einzelnen Partikels mit dem Lagrange-Ansatz verfolgt. Eine Verfolgung wird durchgeführt, indem ein System gewöhnlicher Differentialgleichungen in der Zeit für jedes Partikel gebildet wird, das aus Gleichungen für Position und Geschwindigkeit besteht. Diese Gleichungen werden dann integriert, um die Reaktion der Partikel beim Durchlaufen der Strömungsdomäne zu berechnen. Die Merkmale des Partikelmodellierungsansatzes in Creo Flow Analysis folgen:
• Das diskrete Partikelmodell folgt dem Euler-Lagrange-Ansatz. Die Flüssigkeitsphase wird als Kontinuum behandelt, indem die Kontinuitäts- und Navier-Stokes-Gleichungen gelöst werden. Die dispergierte Phase wird gelöst, indem die Bewegung jedes einzelnen Partikels mithilfe eines Lagrange-Ansatzes verfolgt wird. Der von den Partikeln eingenommene Volumenanteil ist nicht in der Berechnung der kontinuierlichen Phase enthalten.
• Partikel, für die Massenlos (Massless) eingestellt ist, bewegen sich mit dem Flüssigkeitsfluss oder folgen den Stromlinien des Strömungsfelds. Die Partikelgröße oder der Partikelradius wirkt sich nicht auf den Fluss oder die Partikel aus und sind nur zur Anzeige verfügbar.
• Für Partikel, für die Mit Masse (Has Mass) eingestellt wurde, wird die Masse durch die Werte bestimmt, die Sie für den angegebenen Partikelradius oder -durchmesser und die Partikeldichte angeben. Die auf ein Partikel wirkenden Kräfte, die die Bewegung von Partikeln bestimmen, umfassen die Partikel-Fluid-Widerstandskraft (Trägheitskraft) und Gravitation. Die Turbulenzdispersionskräfte an Partikeln werden nicht berücksichtigt. Die Größe der Partikel beeinflusst die Partikel-Fluid-Zugkräfte und das Postprocessing.
• Der Impulsaustausch zwischen der Flüssigkeitsphase und den diskreten Partikelphasen wird durch Folgendes modelliert:
◦ Unidirektionale Kopplung – Nur die Flüssigkeitsphase wirkt sich auf die Bewegungen von Partikeln aus.
◦ Bidirektionale Kopplung – Partikel wirken sich durch Partikel-Fluid-Zugkräfte auch auf den Flüssigkeitsfluss aus.
• Wand-Partikel-Interaktionen werden mit Partikel-Wandmodellen wie Haftung, perfekte Ablenkung und partielle Ablenkung modelliert.
• Während die Flüssigkeitsphase stetig und unstet sein kann, ist die Partikelverfolgung ein transienter Prozess, der die Integration von Partikelpfaden durch die diskrete Domäne umfasst. Bei diesem Ansatz werden einzelne Partikel zu unterschiedlichen Zeitpunkten von bestimmten Positionen freigesetzt oder injiziert. Jedes Partikel wird von seiner Freisetzungsposition bis zum Ziel verfolgt, wo es aus der Domäne entweicht oder bestimmte Integrationsgrenzen erfüllt. Schließlich wird ein Durchschnitt aller Partikelspuren erlangt, und die Partikel-Flüssigkeits-Interaktionen werden als Quellterme der Flüssigkeitsphasen-Impulsgleichungen berechnet.
• Der von Partikeln zurückgelegte Pfad wird mithilfe der zugehörigen Streichlinienverfolgungsmethode im Modul Partikel (Particle) angezeigt.
Partikelbewegungstheorie
Beim Lagrange-Ansatz wird die Partikelbewegung durch den Kraftausgleich am Partikel und die Bedingungen bestimmt, unter denen das Partikel freigesetzt wird (Anfangsbedingungen). Die Bewegungsgleichungen werden für Partikel zuerst auf der Basis des Kraftausgleichs gebildet, um die diskrete Partikelphase zu modellieren. Anschließend geben Sie die Randbedingungen und die Anfangsbedingungen für Partikel an. Schließlich wird die Integration der Partikelbewegungsgleichung für die Partikelverfolgung durchgeführt.
Bewegungsgleichungen für Partikel
• Partikelkraftausgleich
Bei einem diskreten Partikel, das sich in einem kontinuierlichen Flüssigkeitsmedium bewegt, wird die Partikelbewegung durch die auf das Partikel wirkende Nettokraft bestimmt. Nach dem zweiten Newtonschen Gesetz kann der Kraftausgleich im Partikel in der folgenden Lagrange-Formel ausgedrückt werden:
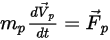
Gleichung 2.366
Dabei gilt:
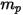 | Partikelmasse (kg) |
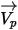 | Partikelgeschwindigkeit m/s |
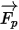 | auf das Partikel ausgeübte Nettokraft (N), die sich auf die Partikelbeschleunigung auswirkt |
Wenn in einem kartesischen Koordinatensystem Folgendes gilt:
Punkt 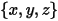 | Position des Partikels |
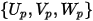 | Geschwindigkeitskomponenten des Partikels |
ist gemäß dem Lagrange-Ansatz die Partikelgeschwindigkeit 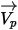 wie folgt definiert:
wie folgt definiert:
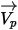 wie folgt definiert:
wie folgt definiert: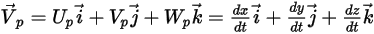
Gleichung 2.367
Bei einem sphärischen Partikel, das ein Volumen 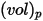 mit der Dichte
mit der Dichte 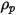 und dem Durchmesser
und dem Durchmesser 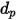 einnimmt (Creo Flow Analysis akzeptiert den Radius als Eingabe), wird die Partikelmasse
einnimmt (Creo Flow Analysis akzeptiert den Radius als Eingabe), wird die Partikelmasse 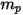 wie folgt berechnet:
wie folgt berechnet:
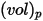 mit der Dichte
mit der Dichte 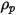 und dem Durchmesser
und dem Durchmesser 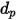 einnimmt (Creo Flow Analysis akzeptiert den Radius als Eingabe), wird die Partikelmasse
einnimmt (Creo Flow Analysis akzeptiert den Radius als Eingabe), wird die Partikelmasse 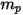 wie folgt berechnet:
wie folgt berechnet: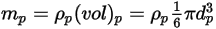
Gleichung 2.368
Zur Nettokraft 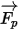 tragen Faktoren wie die Flüssigkeit-zu-Partikel-Widerstandskraft, der Gravitationseffekt und die Kräfte aufgrund der Domänenrotation (Zentripetalkraft und Corioliskraft) bei. Zusätzliche beitragende Faktoren sind weitere Kräfte bedingt durch die Geschwindigkeitsdifferenz zwischen dem Partikel und der Flüssigkeit und die Verdrängung der Flüssigkeit durch das Partikel. In Creo Flow Analysis kann
tragen Faktoren wie die Flüssigkeit-zu-Partikel-Widerstandskraft, der Gravitationseffekt und die Kräfte aufgrund der Domänenrotation (Zentripetalkraft und Corioliskraft) bei. Zusätzliche beitragende Faktoren sind weitere Kräfte bedingt durch die Geschwindigkeitsdifferenz zwischen dem Partikel und der Flüssigkeit und die Verdrängung der Flüssigkeit durch das Partikel. In Creo Flow Analysis kann 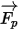 wie folgt ausgedrückt werden:
wie folgt ausgedrückt werden:
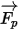 tragen Faktoren wie die Flüssigkeit-zu-Partikel-Widerstandskraft, der Gravitationseffekt und die Kräfte aufgrund der Domänenrotation (Zentripetalkraft und Corioliskraft) bei. Zusätzliche beitragende Faktoren sind weitere Kräfte bedingt durch die Geschwindigkeitsdifferenz zwischen dem Partikel und der Flüssigkeit und die Verdrängung der Flüssigkeit durch das Partikel. In Creo Flow Analysis kann
tragen Faktoren wie die Flüssigkeit-zu-Partikel-Widerstandskraft, der Gravitationseffekt und die Kräfte aufgrund der Domänenrotation (Zentripetalkraft und Corioliskraft) bei. Zusätzliche beitragende Faktoren sind weitere Kräfte bedingt durch die Geschwindigkeitsdifferenz zwischen dem Partikel und der Flüssigkeit und die Verdrängung der Flüssigkeit durch das Partikel. In Creo Flow Analysis kann 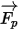 wie folgt ausgedrückt werden:
wie folgt ausgedrückt werden: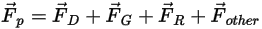
Gleichung 2.369
Dabei gilt:
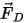 | Widerstandskraft (N) |
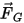 | Gravitationskraft (N) |
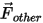 | andere Kräfte wie virtuelle Massenkraft, Druckgradientkraft, vom Benutzer festgelegte Auftriebskraft (n) |
Standardmäßig wird nur die Widerstandskraft auf das Partikel berücksichtigt.
Substituiert man Gleichung 2.369 in Gleichung 2.366 und dividiert dann 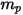 , hat die gelöste Kraftausgleichsgleichung für ein Partikel die folgende Formel:
, hat die gelöste Kraftausgleichsgleichung für ein Partikel die folgende Formel:
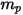 , hat die gelöste Kraftausgleichsgleichung für ein Partikel die folgende Formel:
, hat die gelöste Kraftausgleichsgleichung für ein Partikel die folgende Formel: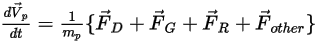
Gleichung 2.370
Der Beitrag jeder einzelnen Kraft muss berechnet werden, um Gleichung 2.370 zu schließen. Nachfolgend sind die Submodelle oder Formeln aufgeführt, die in Creo Flow Analysis übernommen wurden:
◦ Widerstandskraft auf Partikel
Die auf ein Partikel wirkende aerodynamische Widerstandskraft ist proportional zur Phasenschlupfgeschwindigkeit, der Differenz zwischen der Fluid- und der Partikelgeschwindigkeit. Unter der Annahme, dass die Flüssigkeitsgeschwindigkeit an dem Ort, an dem sich das Partikel zu einem bestimmten Zeitpunkt befindet, gleich 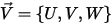 ist, lässt sich die Widerstandskraft wie folgt ausdrücken:
ist, lässt sich die Widerstandskraft wie folgt ausdrücken:
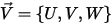 ist, lässt sich die Widerstandskraft wie folgt ausdrücken:
ist, lässt sich die Widerstandskraft wie folgt ausdrücken: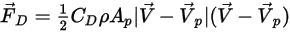
Gleichung 2.371
Dabei gilt:
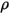 | Flüssigkeitsphasendichte |
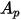 | in Fließrichtung projizierte Fläche des Partikels |
Für ein sphärisches Partikel mit dem Durchmesser 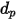 ist
ist 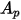 die maximale Querschnittsfläche:
die maximale Querschnittsfläche:
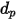 ist
ist 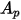 die maximale Querschnittsfläche:
die maximale Querschnittsfläche: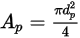
Gleichung 2.372
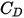 ist der Widerstandskoeffizient, der von der relativen Reynolds-Zahl
ist der Widerstandskoeffizient, der von der relativen Reynolds-Zahl 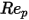 abhängt:
abhängt: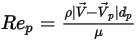
Gleichung 2.373
Dabei ist 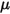 die dynamische Viskosität der Flüssigkeit (PA-s).
die dynamische Viskosität der Flüssigkeit (PA-s).
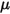 die dynamische Viskosität der Flüssigkeit (PA-s).
die dynamische Viskosität der Flüssigkeit (PA-s).Der Widerstandskoeffizient 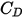 wird eingeführt, um experimentelle Ergebnisse des viskosen Widerstands einer Vollkugel zu berücksichtigen. Es werden verschiedene Modelle oder empirische Korrelationen entwickelt, um die Widerstandsfunktion
wird eingeführt, um experimentelle Ergebnisse des viskosen Widerstands einer Vollkugel zu berücksichtigen. Es werden verschiedene Modelle oder empirische Korrelationen entwickelt, um die Widerstandsfunktion 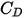 (
(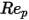 ) zur Schätzung des Flüssigkeit-Partikel-Austauschs zu bestimmen. Für glatte sphärische Partikel stellen neben vielen Modellen die Korrelation nach Morsi und Alexander die vollständigste
) zur Schätzung des Flüssigkeit-Partikel-Austauschs zu bestimmen. Für glatte sphärische Partikel stellen neben vielen Modellen die Korrelation nach Morsi und Alexander die vollständigste 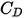 -Funktion dar.
-Funktion dar.
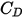 wird eingeführt, um experimentelle Ergebnisse des viskosen Widerstands einer Vollkugel zu berücksichtigen. Es werden verschiedene Modelle oder empirische Korrelationen entwickelt, um die Widerstandsfunktion
wird eingeführt, um experimentelle Ergebnisse des viskosen Widerstands einer Vollkugel zu berücksichtigen. Es werden verschiedene Modelle oder empirische Korrelationen entwickelt, um die Widerstandsfunktion 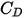 (
(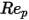 ) zur Schätzung des Flüssigkeit-Partikel-Austauschs zu bestimmen. Für glatte sphärische Partikel stellen neben vielen Modellen die Korrelation nach Morsi und Alexander die vollständigste
) zur Schätzung des Flüssigkeit-Partikel-Austauschs zu bestimmen. Für glatte sphärische Partikel stellen neben vielen Modellen die Korrelation nach Morsi und Alexander die vollständigste 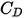 -Funktion dar.
-Funktion dar.Referenzen: S. A. Morsi und A. J. Alexander, "An Investigation of Particle Trajectories in Two-Phase Flow Systems", J. Fluid Mech., 55(2) 193–208, 26. September 1972.
Diese hat den allgemeinen Ausdruck:
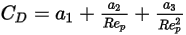
Gleichung 2.374
Dabei sind 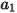 ,
, 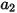 und
und 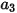 Modellkonstanten, deren Werte von der relativen Reynolds-Zahl abhängen, wie in der folgenden Tabelle dargestellt:
Modellkonstanten, deren Werte von der relativen Reynolds-Zahl abhängen, wie in der folgenden Tabelle dargestellt:
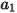 ,
, 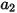 und
und 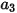 Modellkonstanten, deren Werte von der relativen Reynolds-Zahl abhängen, wie in der folgenden Tabelle dargestellt:
Modellkonstanten, deren Werte von der relativen Reynolds-Zahl abhängen, wie in der folgenden Tabelle dargestellt: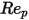 | 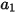 | 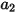 | 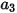 |
0 < 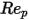 <=0.1 <=0.1 | 0 | 24 | 0 |
0.1 < 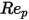 <=1 <=1 | 3.690 | 22.73 | 0.0903 |
1< 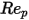 <=10 <=10 | 1.222 | 29.1667 | -3.8889 |
10 < 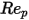 <=100 <=100 | 0.6167 | 46.50 | -116.67 |
100 < 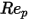 <=1000 <=1000 | 0.3644 | 98.33 | -2778 |
1000 < 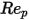 <=5000 <=5000 | 0.357 | 148.62 | -47500 |
5000 < 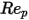 <=10000 <=10000 | 0.46 | -490.546 | 578700 |
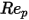 >10000 >10000 | 0.5191 | -1662.5 | 5416700 |
Die Tabelle zeigt, dass bei sehr niedrigen Partikel-Reynolds-Zahlen (viskose Strömung), 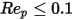 , der Widerstandskoeffizient für den Fluss an sphärischen Partikeln zum Gesetz von Stokes zurückkehrt:
, der Widerstandskoeffizient für den Fluss an sphärischen Partikeln zum Gesetz von Stokes zurückkehrt:
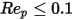 , der Widerstandskoeffizient für den Fluss an sphärischen Partikeln zum Gesetz von Stokes zurückkehrt:
, der Widerstandskoeffizient für den Fluss an sphärischen Partikeln zum Gesetz von Stokes zurückkehrt:
Gleichung 2.375
Wenn dagegen 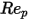 ausreichend groß ist, sodass die Trägheitseffekte die viskosen Effekte beherrschen, ist der Flüssigkeit-Partikel-Fluss im Trägheits- oder Newton-System. In der Tabelle ist zu beobachten, dass der Widerstandskoeffizient weniger abhängig von der relativen Reynolds-Zahl wird. Auch wird häufig eine Konstante des Werts
ausreichend groß ist, sodass die Trägheitseffekte die viskosen Effekte beherrschen, ist der Flüssigkeit-Partikel-Fluss im Trägheits- oder Newton-System. In der Tabelle ist zu beobachten, dass der Widerstandskoeffizient weniger abhängig von der relativen Reynolds-Zahl wird. Auch wird häufig eine Konstante des Werts 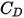 anstelle des vollständigen Modells von Morsi und Alexander verwendet:
anstelle des vollständigen Modells von Morsi und Alexander verwendet:
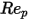 ausreichend groß ist, sodass die Trägheitseffekte die viskosen Effekte beherrschen, ist der Flüssigkeit-Partikel-Fluss im Trägheits- oder Newton-System. In der Tabelle ist zu beobachten, dass der Widerstandskoeffizient weniger abhängig von der relativen Reynolds-Zahl wird. Auch wird häufig eine Konstante des Werts
ausreichend groß ist, sodass die Trägheitseffekte die viskosen Effekte beherrschen, ist der Flüssigkeit-Partikel-Fluss im Trägheits- oder Newton-System. In der Tabelle ist zu beobachten, dass der Widerstandskoeffizient weniger abhängig von der relativen Reynolds-Zahl wird. Auch wird häufig eine Konstante des Werts 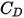 anstelle des vollständigen Modells von Morsi und Alexander verwendet:
anstelle des vollständigen Modells von Morsi und Alexander verwendet: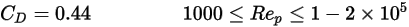
Gleichung 2.376
Im Übergangsbereich zwischen dem viskosen und dem Trägheitssystem, 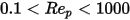 , sind für sphärische Partikel sowohl viskose Effekte als auch Trägheitseffekte wichtig. Daher ist der Widerstandskoeffizient eine komplexe Funktion der relativen Reynolds-Zahl, die anhand des Modells von Morsi und Alexander oder von anderen Korrelationen geschätzt werden kann. Beispiel: Nach dem Modell von Schiller und Naumann gilt:
, sind für sphärische Partikel sowohl viskose Effekte als auch Trägheitseffekte wichtig. Daher ist der Widerstandskoeffizient eine komplexe Funktion der relativen Reynolds-Zahl, die anhand des Modells von Morsi und Alexander oder von anderen Korrelationen geschätzt werden kann. Beispiel: Nach dem Modell von Schiller und Naumann gilt:
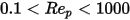 , sind für sphärische Partikel sowohl viskose Effekte als auch Trägheitseffekte wichtig. Daher ist der Widerstandskoeffizient eine komplexe Funktion der relativen Reynolds-Zahl, die anhand des Modells von Morsi und Alexander oder von anderen Korrelationen geschätzt werden kann. Beispiel: Nach dem Modell von Schiller und Naumann gilt:
, sind für sphärische Partikel sowohl viskose Effekte als auch Trägheitseffekte wichtig. Daher ist der Widerstandskoeffizient eine komplexe Funktion der relativen Reynolds-Zahl, die anhand des Modells von Morsi und Alexander oder von anderen Korrelationen geschätzt werden kann. Beispiel: Nach dem Modell von Schiller und Naumann gilt:Referenzen: L. Schiller und Z. Naumann, "Z. Ver. Deutsch. Ing. 77. 318. 1935.
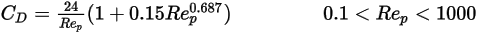
Gleichung 2.377
Die Partikel-Relaxationszeit 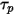 wird eingeführt, um den Ausdruck des Widerstandskraftterms in Gleichung 2.370 zu vereinfachen:
wird eingeführt, um den Ausdruck des Widerstandskraftterms in Gleichung 2.370 zu vereinfachen:
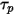 wird eingeführt, um den Ausdruck des Widerstandskraftterms in Gleichung 2.370 zu vereinfachen:
wird eingeführt, um den Ausdruck des Widerstandskraftterms in Gleichung 2.370 zu vereinfachen: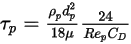
Gleichung 2.378
Wenn Gleichung 2.368, Gleichung 2.371, Gleichung 2.372, Gleichung 2.373 und Gleichung 2.378 kombiniert werden, hat die Widerstandskraft pro Einheit der Partikelmasse folgende Formel:
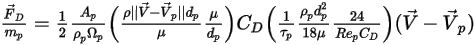
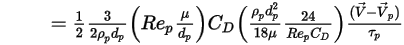
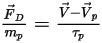
Gleichung 2.379
Daher wird die standardmäßige Partikel-Kraftausgleichsgleichung (nur die Widerstandskraft wird berücksichtigt) folgendermaßen ausgedrückt:
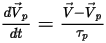
Gleichung 2.380
• Einbeziehung des Gravitationsterms
Standardmäßig wird der Gravitationsterm nicht in die Partikel-Kraftausgleichsgleichung einbezogen. Der Gravitationsterm kann in Creo Flow Analysis aktiviert werden. Bei einem Partikel, das in den Flüssigkeitsfluss eingetaucht ist, führt die Gravitation zu einer Auftriebskraft, die gleich dem Gewicht der durch das Partikel verdrängten Flüssigkeit ist. Angenommen 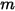 ist die Flüssigkeitsmasse, die durch das Partikel verdrängt wird, und
ist die Flüssigkeitsmasse, die durch das Partikel verdrängt wird, und 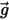 der Gravitationsvektor, ergibt sich die resultierende Kraft wie folgt:
der Gravitationsvektor, ergibt sich die resultierende Kraft wie folgt:
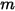 ist die Flüssigkeitsmasse, die durch das Partikel verdrängt wird, und
ist die Flüssigkeitsmasse, die durch das Partikel verdrängt wird, und 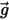 der Gravitationsvektor, ergibt sich die resultierende Kraft wie folgt:
der Gravitationsvektor, ergibt sich die resultierende Kraft wie folgt: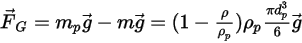
Gleichung 2.381
Oder die Kraft pro Einheit Partikelmasse ist gegeben als:
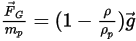
Gleichung 2.382
Und die Kraftausgleichsgleichung hat die folgende Form:
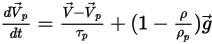
Gleichung 2.383
• Rotationskraft an Partikeln
Bei Flüssigkeitsflüssen des Modells in einem rotierenden Referenzbezugssystem ist der rotationsinduzierte zusätzliche Kraftterm 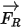 ein wesentlicher Bestandteil der Partikelbeschleunigung. Er umfasst die Wirkung der Coriolis- und Zentripetalkraft:
ein wesentlicher Bestandteil der Partikelbeschleunigung. Er umfasst die Wirkung der Coriolis- und Zentripetalkraft:
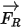 ein wesentlicher Bestandteil der Partikelbeschleunigung. Er umfasst die Wirkung der Coriolis- und Zentripetalkraft:
ein wesentlicher Bestandteil der Partikelbeschleunigung. Er umfasst die Wirkung der Coriolis- und Zentripetalkraft: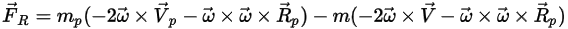
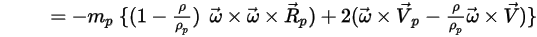
Gleichung 2.384
Oder die Rotationskraft pro Einheit Partikelmasse ist gegeben als:
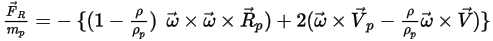
Gleichung 2.385
Dabei gilt:
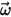 | Winkelgeschwindigkeit des rotierenden Referenzbezugssystems |
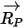 | Vektor, der das Achsenzentrum und die Partikelposition verbindet |
Wenn dieser Kraftterm hinzugefügt wird, lautet die Partikelbilanzgleichung:
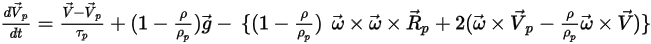
Gleichung 2.386
Gleichung 2.386 steuert die Bewegung eines Partikels in einem Lagrange-System, wenn die Strömung in einem rotierenden Referenzbezugssystem gelöst wird.
Randbedingungen und Anfangsbedingungen für Partikel
Beim Lagrange-Ansatz ist die Partikelverfolgung ein transientes Verfahren. Daher werden die Randbedingungen und Anfangsbedingungen benötigt, um die Bahnkurve der Partikel zu berechnen. Randbedingungen definieren die Partikelreaktion an den Berandungen der Rechendomäne, insbesondere der Partikel-Wand-Interaktionen. Die Anfangsbedingungen bestimmen die Partikelfreisetzung aus Berandungen, einschließlich Freisetzungsposition, -frequenz, -geschwindigkeit, Partikeltyp und -größe (Radius) und Anzahl der Partikel.
Randbedingungen
Creo Flow Analysis liefert eine Randbedingung für die diskrete Phase, um die Reaktion von Partikeln an einer Berandung zu bestimmen. Wenn ein Partikel eine Berandung der Strömungsdomäne (einschließlich physikalische Berandung und Fest-Flüssig-Schnittstelle) erreicht, z.B. eine Wand oder eine Einlassberandung, tritt eines der folgenden Ereignisse ein:
• Partikel reflektiert durch eine elastische oder inelastische Kollision.
• Partikel entweicht durch die Berandung und geht am Punkt des Aufpralls auf die Berandung aus der Berechnung verloren.
• Partikel wird an der Wand gefangen und geht am Punkt des Aufpralls auf die Berandung aus der Berechnung verloren.
• Partikel passiert eine interne Berandungszone, z.B. Lüfter (Fan) oder poröser Sprung (Porous Jump).
• Die Partikel-Rand-Interaktion wird durch benutzerdefinierte Methoden bestimmt, um die Partikelreaktion beim Auftreffen auf die Berandung zu modellieren.
Auf der Basis der Partikelreaktion an Berandungen werden die Flow-Randbedingungen und -Schnittstellen in drei Arten von Randbedingungen für diskrete Partikel neu gruppiert: Offen (Open), Symmetrie (Symmetry) und Wand (Wall).
• Diskrete Partikelrandbedingung "Offen" (Open)
Partikel oder Stromlinien können die Rechendomäne verlassen. Eine offene Berandung ist eine Einlass- oder Auslassberandung der Flüssigkeitsphase im Euler-System. Sie kann auch auf Flow-Randbedingungen wie Wand und Symmetrie angewendet werden. An einer offenen Partikelberandung tritt das Partikel je nach Partikelgeschwindigkeitsrichtung in die Domäne ein oder verlässt diese.
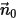 sei der Einheitsnormalenvektor zur offenen Berandung, der weg von der Rechendomäne zeigt, mit der Partikelberandungsgeschwindigkeit
sei der Einheitsnormalenvektor zur offenen Berandung, der weg von der Rechendomäne zeigt, mit der Partikelberandungsgeschwindigkeit 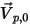 . Wenn
. Wenn 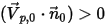 , zeigt der Geschwindigkeitsvektor
, zeigt der Geschwindigkeitsvektor  weg von der Rechendomäne. Das gibt an, dass das Partikel durch die Berandung entweicht und am Punkt des Aufpralls auf der Berandung aus der Berechnung verlorengeht.
weg von der Rechendomäne. Das gibt an, dass das Partikel durch die Berandung entweicht und am Punkt des Aufpralls auf der Berandung aus der Berechnung verlorengeht.• Partikelrandbedingung "Symmetrie" (Symmetry)
Wenn ein Partikel oder eine Streichlinie in der Rechendomäne auf eine diskrete Symmetrieberandung trifft, reflektiert die Randbedingung diese wieder zurück in die Domäne. Bei der diskreten Partikelphase entspricht eine Partikelrandbedingung "Symmetrie" (Symmetry) typischerweise einer Flow-Symmetrie im Euler-System. Sie kann auch ein Ort für die Partikelfreisetzung sein.
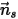 sei der Einheitsvektor normal zur Symmetrie am Punkt
sei der Einheitsvektor normal zur Symmetrie am Punkt 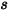 der Symmetrie, der weg von der Symmetrie zur Rechendomäne zeigt.
der Symmetrie, der weg von der Symmetrie zur Rechendomäne zeigt. 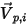 und
und 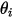 werden eingeführt, um den Partikel-Aufprallgeschwindigkeitswinkel an der Symmetrie-Partikelberandung anzugeben, wie in der folgenden Abbildung dargestellt. Da das Partikel von der Symmetrie reflektiert wird, bleibt seine gesamte kinetische Energie erhalten: Die tangentiale Geschwindigkeit bleibt gleich, während die normale Geschwindigkeitskomponente nur das Vorzeichen ändert. Die Partikelrandbedingung "Symmetrie" (Symmetry) wird ausgedrückt als:
werden eingeführt, um den Partikel-Aufprallgeschwindigkeitswinkel an der Symmetrie-Partikelberandung anzugeben, wie in der folgenden Abbildung dargestellt. Da das Partikel von der Symmetrie reflektiert wird, bleibt seine gesamte kinetische Energie erhalten: Die tangentiale Geschwindigkeit bleibt gleich, während die normale Geschwindigkeitskomponente nur das Vorzeichen ändert. Die Partikelrandbedingung "Symmetrie" (Symmetry) wird ausgedrückt als: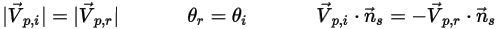
Gleichung 2.387
Dabei gilt:
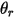 | Winkel am Punkt 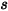 : der Symmetrie (Grad) : der Symmetrie (Grad) |
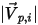 | Betrag der Partikel-Aufprallgeschwindigkeit (m/s) |
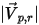 | Betrag der reflektierten Partikelgeschwindigkeit (m/s) |
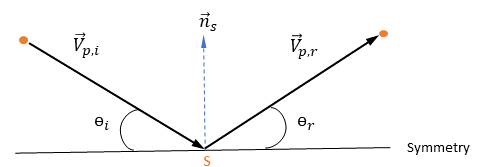
• Partikelrandbedingung "Wand" (Wall)
Bei Flüssigkeitströpfchen hängt die Tröpfchen-Wand-Interaktion von der Wandtemperatur, dem Wandmaterial und der Wandrauheit, dem Aufprallwinkel und der Aufprallgeschwindigkeit, dem Vorhandensein eines Wandfilms und verschiedenen anderen Parametern ab. Anschließend werden verschiedene Untermodelle verwendet, um die verschiedenen Systeme von Wand-Partikel-Interaktionen zu reproduzieren und die Auswirkungen von Strömungsparametern und Wand-Randbedingungen zu berücksichtigen.
Im aktuellen diskreten Partikelmodell wird davon ausgegangen, dass die Form, die Größe und die Masse der Partikel unverändert bleiben. Außerdem werden die Flüssigkeit und die Partikel als im thermischen Gleichgewicht stehend betrachtet. Daher beschreibt ein einfacher Ansatz den Prozess von Partikeln (mit Masse), die mit Wänden kollidieren: Während des Kollisionsprozesses tauschen Partikel Impuls nur mit der Wand aus, und die Partikel interagieren in einer von drei Arten und Weisen mit der Wand. Die drei Arten und Weisen sind "Perfekte Ablenkung", "Haftung" und "Partielle Ablenkung".
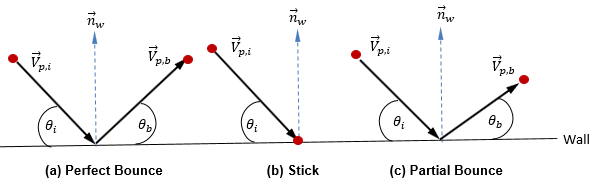
◦ Perfekte Ablenkung – Ein Partikel oder eine Streichlinie reflektiert, wenn es bzw. sie auf eine Wand trifft. Der Impuls und die kinetische Energie des Partikels bleiben perfekt erhalten. Der Einfallswinkel ist gleich dem Reflexionswinkel, während die normale Geschwindigkeitskomponente der Wand das Vorzeichen ändert:
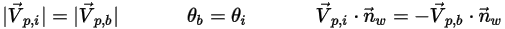
Gleichung 2.388
Dabei gilt:
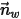 | Normalen-Einheitsvektor der Wand |
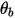 | Winkel an der Wandberandung (Grad) |
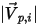 | Betrag der Partikel-Aufprallgeschwindigkeit (m/s) |
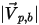 | Betrag der Partikel-Ablenkung-Geschwindigkeit (m/s) |
◦ Haftung – Ein Partikel kollidiert mit der Wand, verliert seinen gesamten Impuls und seine gesamte Energie und bleibt an der Wand haften:
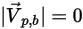
Ohne Berücksichtigung der Partikelakkumulation entlang der Wand geht das Partikel dann am Punkt des Aufpralls auf die Berandung vollständig aus der Berechnung verloren.
◦ Partielle Ablenkung – Wand-Partikel-Bedingung zwischen "Perfekte Ablenkung" und "Haftung". Ein Partikel oder eine Streichlinie wird von einer Wand abgelenkt, verliert jedoch einen Teil der Energie in normaler, tangentialer oder sowohl in normaler als auch in tangentialer Richtung. Der Impuls und die kinetische Energie des Partikels bleiben perfekt erhalten und der Einfallswinkel ist in der Regel größer als der Reflexionswinkel:
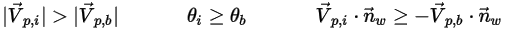
Der Energieverlust durch Partikel-Wand-Interaktion wird durch Benutzereingaben festgelegt:
▪ Normaler Energieverlust – Gibt den Verlust der normalen Komponente der kinetischen Energie eines Partikels an der Wand an.
▪ Tangentialer Energieverlust – Gibt den Verlust der tangentialen Komponente der kinetischen Energie eines Partikels an der Wand an.
In Creo Flow Analysis wird durch die angegebenen Werte für die maximale und die minimale normale Geschwindigkeit festgelegt, ob ein Partikel abgelenkt wird oder haften bleibt. Unter der Annahme, dass 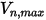 die angegebene maximale normale Geschwindigkeit des Partikels und
die angegebene maximale normale Geschwindigkeit des Partikels und 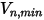 die angegebene minimale normale Geschwindigkeit des Partikels ist, gelten die folgenden Bedingungen:
die angegebene minimale normale Geschwindigkeit des Partikels ist, gelten die folgenden Bedingungen:
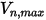 die angegebene maximale normale Geschwindigkeit des Partikels und
die angegebene maximale normale Geschwindigkeit des Partikels und 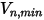 die angegebene minimale normale Geschwindigkeit des Partikels ist, gelten die folgenden Bedingungen:
die angegebene minimale normale Geschwindigkeit des Partikels ist, gelten die folgenden Bedingungen:▪ Wenn 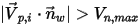 oder
oder 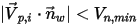 , wird das Partikel von der Wand abgelenkt.
, wird das Partikel von der Wand abgelenkt.
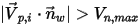 oder
oder 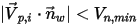 , wird das Partikel von der Wand abgelenkt.
, wird das Partikel von der Wand abgelenkt.▪ Wenn 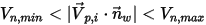 , bleibt das Partikel an der Wand haften.
, bleibt das Partikel an der Wand haften.
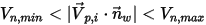 , bleibt das Partikel an der Wand haften.
, bleibt das Partikel an der Wand haften.Die Partikel-Wand-Interaktionsmodelle gelten nur für die Partikel, für die Hat Masse (Has Mass) festgelegt ist. Ein massenloses Partikel folgt der Fluss-Stromlinie entlang den Wänden.
Beachten Sie, dass die Partikel-Wandberandungen externe Wände und Flüssigkeit-Festkörper-Schnittstellen sein können. Wie bei den Randbedingungen "Offen" (Open) und "Symmetrie" (Symmetry) für Partikel können Partikel von einer Wandberandung freigesetzt werden.
Anfangsbedingungen (Partikel freisetzen)
Die Anfangsbedingungen geben die Anfangswerte für alle abhängigen diskreten Phasenvariablen an, die die momentanen Bedingungen eines einzelnen Partikels beschreiben. Für die Partikelverfolgung des Lagrange-Systems beinhaltet das Verfahren zum Bestimmen der Anfangsbedingungen die Partikelfreisetzung (Frequenz und Verteilung) von Berandungen (Offen, Symmetrie, Wand und Schnittstelle) und die Zuweisung von Eigenschaften für jedes Partikel.
Wenn Sie Release Particle aktivieren, sind die folgenden Parameter oder Variablen die Anfangsbedingungen für die Partikelbewegungen:
Integration der Partikelbewegungsgleichung
Zur Verfolgung der Partikelbewegung werden die Bahnkurvengleichungen jedes Partikels analytisch oder numerisch in einem Lagrange-System gelöst (integriert). Aus Gleichung 2.367 und Gleichung 2.386 werden die Bewegungsgleichungen umgeformt in:
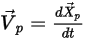
Gleichung 2.391
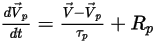
Gleichung 2.392
Dabei gilt:
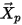 | Positionsvektor des Partikels |
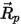 | enthält Beschleunigungen aufgrund aller anderen Kräfte außer der Widerstandskraft wie Gravitation, Rotationseffekte usw. |
Gleichung 2.391 und Gleichung 2.392 sind ein Satz von gekoppelten gewöhnlichen Differentialgleichungen. Bei gegebenen Anfangs- und Randbedingungen wird die Partikelverschiebung, Gleichung 2.391, anhand der Euler-Vorwärts-Integration der Partikelgeschwindigkeit über den Zeitschritt 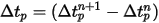 berechnet:
berechnet:
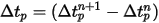 berechnet:
berechnet: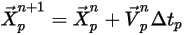
Gleichung 2.393
Dabei gilt:
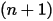 | neue Werte |
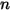 | aktuelle Werte |
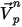 | Partikelgeschwindigkeit beim aktuellen Zeitschritt |
Beim ersten Zeitschritt
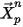 | Freisetzungsposition |
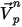 | Anfangsgeschwindigkeit |
Dabei gilt:

Gleichung 2.394
Bei dieser Vorwärts-Integrationsmethode wird davon ausgegangen, dass die Partikelgeschwindigkeit, die zu Beginn des Zeitschritts berechnet wird, über den gesamten Schritt vorherrscht. Am Ende des Zeitschritts wird die neue Partikelgeschwindigkeit durch Lösen des Partikelimpulses, Gleichung 2.392, berechnet. Unter der Annahme, dass 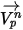 ,
, 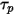 und
und 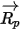 über den Zeitraum
über den Zeitraum 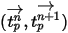 hinweg konstant sind und die Flüssigkeitseigenschaften vom Beginn des Zeitschritts zum Zeitpunkt
hinweg konstant sind und die Flüssigkeitseigenschaften vom Beginn des Zeitschritts zum Zeitpunkt 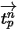 übernommen werden, lautet die analytische Lösung der Gleichung 2.392 folgendermaßen:
übernommen werden, lautet die analytische Lösung der Gleichung 2.392 folgendermaßen:
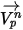 ,
, 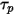 und
und 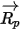 über den Zeitraum
über den Zeitraum 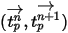 hinweg konstant sind und die Flüssigkeitseigenschaften vom Beginn des Zeitschritts zum Zeitpunkt
hinweg konstant sind und die Flüssigkeitseigenschaften vom Beginn des Zeitschritts zum Zeitpunkt 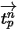 übernommen werden, lautet die analytische Lösung der Gleichung 2.392 folgendermaßen:
übernommen werden, lautet die analytische Lösung der Gleichung 2.392 folgendermaßen: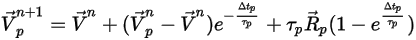
Gleichung 2.395
Zur Bewertung von 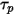 und
und 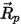 werden Flüssigkeitsvariablen wie Dichte, Viskosität und Geschwindigkeit an der Position des Partikels benötigt. Sie werden als Zellenwerte der Flüssigkeitsphase betrachtet, in der sich das Partikel derzeit befindet. Obwohl dieses analytische Lösungsverfahren effizient ist, kann es für große Zeitschritte und in Situationen ungenau werden, in denen sich die Partikel nicht im hydrodynamischen Gleichgewicht mit dem kontinuierlichen Flüssigkeitsfluss befinden. In einem solchen Fall integrieren die numerischen Lösungsverfahren Gleichung 2.392.
werden Flüssigkeitsvariablen wie Dichte, Viskosität und Geschwindigkeit an der Position des Partikels benötigt. Sie werden als Zellenwerte der Flüssigkeitsphase betrachtet, in der sich das Partikel derzeit befindet. Obwohl dieses analytische Lösungsverfahren effizient ist, kann es für große Zeitschritte und in Situationen ungenau werden, in denen sich die Partikel nicht im hydrodynamischen Gleichgewicht mit dem kontinuierlichen Flüssigkeitsfluss befinden. In einem solchen Fall integrieren die numerischen Lösungsverfahren Gleichung 2.392.
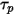 und
und 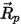 werden Flüssigkeitsvariablen wie Dichte, Viskosität und Geschwindigkeit an der Position des Partikels benötigt. Sie werden als Zellenwerte der Flüssigkeitsphase betrachtet, in der sich das Partikel derzeit befindet. Obwohl dieses analytische Lösungsverfahren effizient ist, kann es für große Zeitschritte und in Situationen ungenau werden, in denen sich die Partikel nicht im hydrodynamischen Gleichgewicht mit dem kontinuierlichen Flüssigkeitsfluss befinden. In einem solchen Fall integrieren die numerischen Lösungsverfahren Gleichung 2.392.
werden Flüssigkeitsvariablen wie Dichte, Viskosität und Geschwindigkeit an der Position des Partikels benötigt. Sie werden als Zellenwerte der Flüssigkeitsphase betrachtet, in der sich das Partikel derzeit befindet. Obwohl dieses analytische Lösungsverfahren effizient ist, kann es für große Zeitschritte und in Situationen ungenau werden, in denen sich die Partikel nicht im hydrodynamischen Gleichgewicht mit dem kontinuierlichen Flüssigkeitsfluss befinden. In einem solchen Fall integrieren die numerischen Lösungsverfahren Gleichung 2.392.Partikel-Fluid-Kopplung
Im Euler-Lagrange-Ansatz wird davon ausgegangen, dass der kontinuierliche Flüssigkeitsfluss die Partikelreaktion durch Kräfte, Wärme und Massenübergang beeinflusst. Beispielsweise betrifft der Kraftterm 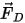 in der Partikel-Kraftausgleichsgleichung, Gleichung 2.370, die aerodynamische Widerstandskraft der Strömung am Partikel. Obwohl die Partikelphase als diskret betrachtet wird und die Flüssigkeit nicht im Volumen verdrängt, können die Partikel durch den Austausch von Impuls und möglicherweise Masse und Wärme einen entgegenwirkenden Einfluss auf den Flüssigkeitsfluss ausüben. Die Wirkung der Partikel auf den Fluss wird als Partikel-Fluid-Kopplung bezeichnet. Sie hat zwei Kategorien:
in der Partikel-Kraftausgleichsgleichung, Gleichung 2.370, die aerodynamische Widerstandskraft der Strömung am Partikel. Obwohl die Partikelphase als diskret betrachtet wird und die Flüssigkeit nicht im Volumen verdrängt, können die Partikel durch den Austausch von Impuls und möglicherweise Masse und Wärme einen entgegenwirkenden Einfluss auf den Flüssigkeitsfluss ausüben. Die Wirkung der Partikel auf den Fluss wird als Partikel-Fluid-Kopplung bezeichnet. Sie hat zwei Kategorien:
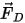 in der Partikel-Kraftausgleichsgleichung, Gleichung 2.370, die aerodynamische Widerstandskraft der Strömung am Partikel. Obwohl die Partikelphase als diskret betrachtet wird und die Flüssigkeit nicht im Volumen verdrängt, können die Partikel durch den Austausch von Impuls und möglicherweise Masse und Wärme einen entgegenwirkenden Einfluss auf den Flüssigkeitsfluss ausüben. Die Wirkung der Partikel auf den Fluss wird als Partikel-Fluid-Kopplung bezeichnet. Sie hat zwei Kategorien:
in der Partikel-Kraftausgleichsgleichung, Gleichung 2.370, die aerodynamische Widerstandskraft der Strömung am Partikel. Obwohl die Partikelphase als diskret betrachtet wird und die Flüssigkeit nicht im Volumen verdrängt, können die Partikel durch den Austausch von Impuls und möglicherweise Masse und Wärme einen entgegenwirkenden Einfluss auf den Flüssigkeitsfluss ausüben. Die Wirkung der Partikel auf den Fluss wird als Partikel-Fluid-Kopplung bezeichnet. Sie hat zwei Kategorien:• Unidirektionale Kopplung
Die unidirektionale Kopplung ermöglicht es der Flüssigkeit, die Bahnkurven von Partikeln zu beeinflussen, aber die Partikel wirken sich nicht auf die Flüssigkeit aus. Bei masselosen Partikeln ist die Partikel-Flüssigkeit-Interaktion eine unidirektionale Kopplung: Die Partikel bewegen sich zusammen mit dem Flüssigkeitsfluss. Bei Partikeln mit Masse kann eine unidirektionale Kopplung eine akzeptable Annäherung in Flüssen mit geringen dispergierten Phasenlasten sein, bei denen Partikel einen vernachlässigbaren Einfluss auf den Flüssigkeitsfluss haben.
Für die kontinuierliche Flüssigkeitsphase wird das Strömungsfeld als einphasiger Flüssigkeitsfluss ohne die Existenz einer dispergierten Partikelphase berechnet. Die Partikelbewegung wird dann basierend auf dem berechneten Strömungsfeld und den Anfangsbedingungen verfolgt. Bei einem stationären Fluss geschieht die Partikelverfolgung, nachdem die konvergierte Flusslösung der kontinuierlichen Phase durch Lösen von Kontinuitäts- und Navier-Stokes-Gleichungen erreicht wurde. Bei einer transienten Strömungssimulation werden die Partikelbewegungen am Ende jedes Zeitschritts der Strömungsimulation verfolgt.
• Bidirektionale Kopplung
Bei Partikeln mit Masse ermöglicht die bidirektionale Kopplung, dass die Flüssigkeit die Bahnkurven von Partikeln beeinflusst. Sie berücksichtigt auch die Wirkung von Partikeln auf die kontinuierliche Flüssigkeitsphase. Ohne Einbeziehung von Masse- und Wärmeübertragung betrifft die bidirektionale Interaktion zwischen der Flüssigkeit und den Partikeln nur den Impulsaustausch. Der Impuls, der von der kontinuierlichen Phase in die diskrete Phase übertragen wird, wird berechnet, indem der Impuls verfolgt wird, den jedes einzelne Partikel gewinnt oder verliert, wenn es ein Kontrollvolumen durchläuft. Bei der bidirektionalen Kopplung muss auch der Partikel-Fluid-Impulsaustausch in die Fluid-Impuls-Gleichungen eingeschlossen werden, um die Wirkung der Bahnkurven der diskreten Phase auf das Kontinuum zu berücksichtigen. Aus Gleichung 2.386 berücksichtigt nur die Widerstandskraft den Partikel-Fluid-Impulsaustausch und wird zu den Impulsgleichungen hinzugefügt. Es ist zu beachten, dass bei masselosen Partikeln keine Austauschterme zwischen dem Flüssigkeitsfluss und diesen berechnet werden, sodass die Bahnkurven der diskreten Phase keine Auswirkungen auf das Kontinuum haben.
Die Widerstandskraft wird für jedes Partikel, das sich durch den Fluss bewegt, im Kontrollvolumen angewendet, wo sich das Partikel während des Zeitschritts befindet, um die Partikel-Fluid-Widerstandswirkungen in die Impulsgleichungen der kontinuierlichen Phase aufzunehmen. Für das Partikel 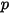 wird die Impulsquelle aufgrund des Widerstands
wird die Impulsquelle aufgrund des Widerstands 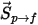 durch die folgende Differentialgleichung berechnet:
durch die folgende Differentialgleichung berechnet:
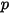 wird die Impulsquelle aufgrund des Widerstands
wird die Impulsquelle aufgrund des Widerstands 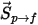 durch die folgende Differentialgleichung berechnet:
durch die folgende Differentialgleichung berechnet: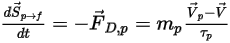
Gleichung 2.396
Und die Partikelquelle zur kontinuierlichen Phase ist der Quellterm 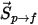 , der mit der Zahl der Flussrate für dieses Partikel (der Massenstrom dividiert durch die Masse des Partikels) multipliziert wird:
, der mit der Zahl der Flussrate für dieses Partikel (der Massenstrom dividiert durch die Masse des Partikels) multipliziert wird:
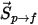 , der mit der Zahl der Flussrate für dieses Partikel (der Massenstrom dividiert durch die Masse des Partikels) multipliziert wird:
, der mit der Zahl der Flussrate für dieses Partikel (der Massenstrom dividiert durch die Masse des Partikels) multipliziert wird: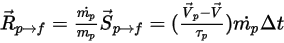
Gleichung 2.397
Dabei gilt:
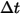 | Zeitschritt |
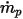 | Partikel-Massenstrom |
Unter der Annahme, dass 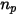 die Anzahl der Partikel ist, die ein Kontrollvolumen im Zeitschritt
die Anzahl der Partikel ist, die ein Kontrollvolumen im Zeitschritt 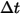 durchlaufen, lautet der Partikel-zu-Fluid-Quellterm insgesamt folgendermaßen:
durchlaufen, lautet der Partikel-zu-Fluid-Quellterm insgesamt folgendermaßen:
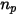 die Anzahl der Partikel ist, die ein Kontrollvolumen im Zeitschritt
die Anzahl der Partikel ist, die ein Kontrollvolumen im Zeitschritt 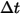 durchlaufen, lautet der Partikel-zu-Fluid-Quellterm insgesamt folgendermaßen:
durchlaufen, lautet der Partikel-zu-Fluid-Quellterm insgesamt folgendermaßen: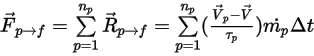
Gleichung 2.398
Mit dem Hinzufügen der Fluid-Partikel-Widerstandskraft lauten die zugrunde liegenden Gleichungen, die für die kontinuierliche Phase gelöst werden, nun folgendermaßen:
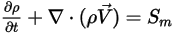
Gleichung 2.399
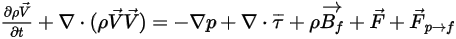
Gleichung 2.400
Bei einer unidirektionalen Kopplung 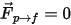 wird die kontinuierliche Flüssigkeitsphase durch die Kontinuitäts- und Impulsgleichungen für die exakte Einzelphase beschrieben. Bei einer bidirektionalen Kopplung kommt zusätzlich der Quellterm für die Partikel-zu-Fluid-Widerstandskraft hinzu. Gleichung 2.399 und Gleichung 2.400 werden in identischer Weise wie beim einphasigen Fluss gelöst.
wird die kontinuierliche Flüssigkeitsphase durch die Kontinuitäts- und Impulsgleichungen für die exakte Einzelphase beschrieben. Bei einer bidirektionalen Kopplung kommt zusätzlich der Quellterm für die Partikel-zu-Fluid-Widerstandskraft hinzu. Gleichung 2.399 und Gleichung 2.400 werden in identischer Weise wie beim einphasigen Fluss gelöst.
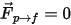 wird die kontinuierliche Flüssigkeitsphase durch die Kontinuitäts- und Impulsgleichungen für die exakte Einzelphase beschrieben. Bei einer bidirektionalen Kopplung kommt zusätzlich der Quellterm für die Partikel-zu-Fluid-Widerstandskraft hinzu. Gleichung 2.399 und Gleichung 2.400 werden in identischer Weise wie beim einphasigen Fluss gelöst.
wird die kontinuierliche Flüssigkeitsphase durch die Kontinuitäts- und Impulsgleichungen für die exakte Einzelphase beschrieben. Bei einer bidirektionalen Kopplung kommt zusätzlich der Quellterm für die Partikel-zu-Fluid-Widerstandskraft hinzu. Gleichung 2.399 und Gleichung 2.400 werden in identischer Weise wie beim einphasigen Fluss gelöst.