Setting Tolerances
Ensure that the default tolerances are appropriate for your designs. You can view and edit the current default settings in the Options dialog box.
1. Click Applications > EZ Tolerance Analysis. The EZ Tolerance tab opens.
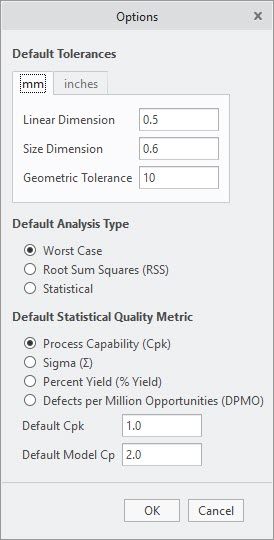
2. Click EZ Tolerance > Options . The Options dialog box opens. In the Default Tolerances area, mm tab is selected by default.
3. Do one of the following:
◦ Specify the default Linear Dimension, Size Dimension, and Geometric Tolerance in millimeters, that complies with the Metric (SI) system.
◦ Click inches to open the inches tab. Specify the tolerances in inches, that comply with the US Customary (USC) system.
|  The tolerance defined in the Options dialog box is converted to the default unit system used for a part in the assembly, if the part is defined in any other unit system. For example, if one of the parts in your stackup has units defined in cm, and the default tolerance for Linear Dimension on the mm tab is 0.1, then any linear dimensions defined in the subject part will have a default tolerance of 0.01 cm. The linear and size dimensions have symmetric ± tolerances. |
4. In the Default Analysis Type area, select one of the following types to be used for each new stackup definition:
◦ Worst-Case
◦ Root Sum Squares (RSS)
◦ Statistical
The analysis type is also referred to as target quality. You can change the type for each stackup. For more information about the differences among these types, see
Types of Tolerance Stackup Analyses.
5. In the Default Statistical Quality Metric area, select one of the following metrics used for your statistical analyses and the associated quality objective:
◦ Process Capability (Cpk)
◦ Sigma (∑)
◦ Percent Yield (% Yield)
◦ Defects per Million Opportunities (DMPO)
6. Specify the default value for the Default Statistical Quality Metric that you have selected in the previous step.
7. Specify the value for the Default Model Cp. The Default Model Cp option controls the default assumption defining the statistical distributions of each dimension in the stackup.